今天的题目是最短公共超序列,如果一个字符串s在删除某些字符后形成t,那么我们说s是t的超序列,现在给定两个字符串str1与str2,返回str1与str2的最长公共超序列,如果有多个的话返回任意一个即可。
大家好,我是小风哥,今天这篇文章会开启动态规划这个主题,动态规划是算法中非常重要的思想之一。
今天的题目是最短公共超序列,如果一个字符串s在删除某些字符后形成t,那么我们说s是t的超序列,现在给定两个字符串str1与str2,返回str1与str2的最长公共超序列,如果有多个的话返回任意一个即可。
假设str1为"abac",str2为“cab”,那么这两个字符串的最短公共超序列是“cabac”;而如果str1为“bc”,str2为“cab”,那么最短公共超序列是“cabc”或者“bcab”。
想一想该怎样解决问题。
子问题与选择
动态规划类问题的关键在于找出子问题以及子问题与原始问题的关联,要想找出子问题就需要知道每一步的选择是什么。
在这个问题中如果str1=“abec”、str2=“aecd”,因为st1与str2的第一个字符相同,那么我们知道字符‘a’一定是最短公共超序列中的一个,这样str1就变为了“bec”,str2就变为了“ecd”,而这个问题本质上和原始问题没有区别,就这样我们找到了子问题。
现在,str1=“bec”和str2=“ecd”的第一个字符不再相等该怎么办呢?很简单:
超序列中包含str1的第一个字符,这样str1就变为了“ec”,str2依然是“ecd”,假设此时str1与str2的最短公共超序列为supers1
超序列中包含str2的第一个字符,这样str1依然是“bec”,str2就变为了“cd”,假设此时str1与str2的最短公共超序列为supers2
原始问题的最长公共超序列一定是supers1与supers2中最短的那一个。
现在我们找到了原始问题与子问题的关联。
状态空间树
基于上述分析,我们可以很容易的画出这样的状态空间树:
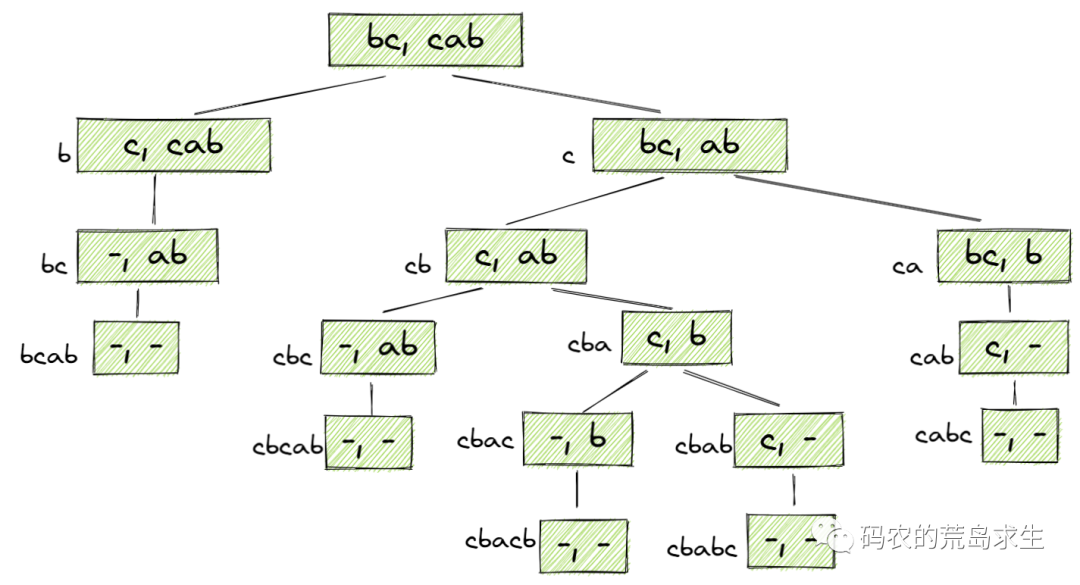
上图中每一个方框都代码一个子问题,如果某个子问题中的两个字符串的首字符不相等那么会衍生出两个新的的子问题,超序列要么使用str1的第一个字符,要么使用str2的第一个字符;而如果str1与str2的首字符相同,那么超序列中只需要新增该字符即可。
该状态空间树的叶子节点为所有str1与str2都为空,此时经过从根节点到叶子结点一路的选择我们就得到了其对应的超序列,从上图看有两种最短公共超序列“bcab”与“cabc”,长度都是4。
从这棵状态空间树中你可以轻易的看到原始问题是如何分解为子问题的以及如果利用子问题的解来构建原始问题的解。
图中每个方框代表一个子问题,决定子问题的只有两个元素,str1与str2首字符的在各自对应字符串的起始位置i和j,因此我们定义递归函数scs(shortest common supersequence的缩写):
该递归函数的含义是字符串str1[i, str1.length()-1]与字符串str2[j, str2.length()-1]的最短公共超序列的长度是多少。
基于上述分析与画出的状态空间树你可以很容易的写出其递归实现:
string str1;
string str2;
int scs(int i, int j) {
// 递归出口1:str1已经为空,超序列只需要包含str2剩下的部分即可
if (i == str1.length()) return str2.length() - j;
// 递归出口2:str2已经为空,超序列只需要包含str1剩下的部分即可
if (j == str2.length()) return str1.length() - i;
// 如果两个字符串的首字符相同,当前问题的解等于子问题的解加1
if (str1[i] == str2[j]) return scs(str1, i + 1, str2, j + 1) + 1;
// 否则当前问题的解等于两个子问题解较小的那一个加1
return min(scs(i + 1, j), scs(i, j + 1)) + 1;
}
可以看到实际上我们只需要四行代码就可以搞定问题,(注意看该递归实现,和最长回文子串这个示例的实现在形式上几乎完全相同,是不是很有趣)。
在这这里将str1与str2作为全局变量,这样你可以清楚的看到递归函数scs的返回值只依赖于参数i和j,而参数i的取值属于[0, str1.length()],j的取值属于[0, str2.length()],因此参数i和j的组合最多只有(str1.length() + 1) * (str2.length() + 1) 个。
重复子问题
再来观察下上述递归代码的形成的状态空间树:
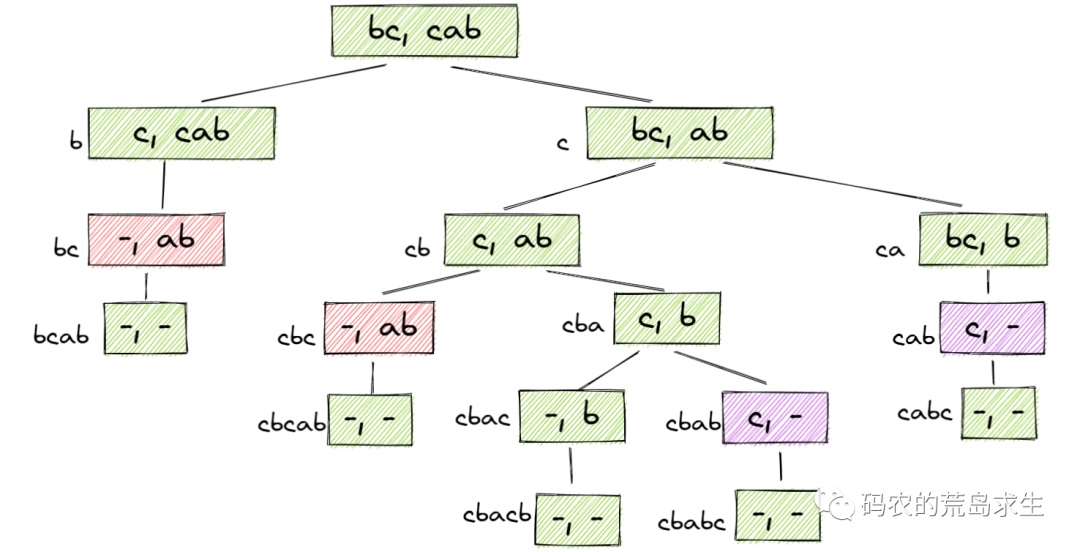
这里存在着一些完全相同的子问题,这些子问题会被重复计算,因此我们可以将子问题解记录下来,当再次遇到该子问题时直接返回结果即可:
string str1;
string str2;
vector<vector<int>> cache;
int scs(int i, int j) {
if (i == str1.length()) return str2.length() - j;
if (j == str2.length()) return str1.length() - i;
if (cache[i][j]) return cache[i][j];
int res;
if (str1[i] == str2[j])
res = scs(str1, i + 1, str2, j + 1) + 1;
else
res = min(scs(i + 1, j), scs(i, j + 1)) + 1;
return cache[i][j] = res;
}
增加cache后每个子问题只被计算一次,这实际上就是递归版的动态规划代码了。
动态规划实现
接下来我们着手将自顶向下的递归代码转为自底向上的动态规划代码。
既然子问题的个数就只有这么多,因此可以使用数组dp来保存子问题解,注意看上述递归函数只依赖两个参数,因此数组dp是二维的,即(str1.length() + 1) * (str2.length() + 1)的二维数组:
vector<vector<int>>dp(str1.length() + 1, vector<int>(str2.length() + 1, 0));
接下来就是最小子问题是什么,注意观察上述两个递归出口,可以看到最小子问题分别是str1与str2为空的情况,基于这两种情况我们可以很容易的构建出最小子问题解,将递归代码中的:
if (i == str1.length()) return str2.length() - j;
if (j == str2.length()) return str1.length() - i;
转为:
for (int j = str2.length() - 1; j >= 0; j--)
dp[str1.length()][j] = str2.length() - j;
for (int i = str1.length() - 1; i >= 0; i--)
dp[i][str2.length()] = str1.length() - i;
最后我们手动利用两个for循环构造出所有i和j的组合,将递归函数中除去递归出口的这一部分:
if (str1[i] == str2[j]) return scs(str1, i + 1, str2, j + 1) + 1;
return min(scs(str1, i + 1, str2, j), scs(str1, i, str2, j + 1)) + 1;
直接放到两个for循环之中,并且将递归调用转为对数组dp的读写:
for (int i = str1.length() - 1; i >= 0; i--) {
for (int j = str2.length() - 1; j >= 0; j--) {
if (str1[i] == str2[j])
dp[i][j] = dp[i + 1][j + 1] + 1;
else
dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) + 1;
}
}这样完整的实现代码为:
int shortestCommonSupersequence(string str1, string str2) {
vector<vector<int>>dp(str1.length() + 1, vector<int>(str2.length() + 1, 0));
for (int j = str2.length() - 1; j >= 0; j--)
dp[str1.length()][j] = str2.length() - j;
for (int i = str1.length() - 1; i >= 0; i--)
dp[i][str2.length()] = str1.length() - i;
for (int i = str1.length() - 1; i >= 0; i--) {
for (int j = str2.length() - 1; j >= 0; j--) {
if (str1[i] == str2[j])
dp[i][j] = dp[i + 1][j + 1] + 1;
else
dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) + 1;
}
}
return dp[0][0];
}