尽管取得了很多显著的成就，但训练深度神经网络（DNN）的实践进展在很大程度上独立于理论依据。大多数成功的现代 DNN 依赖残差连接和归一化层的特定排列，但如何在新架构中使用这些组件的一般原则仍然未知，并且它们在现有架构中的作用也依然未能完全搞清楚。
残差架构是最流行和成功的，最初是在卷积神经网络（CNN）的背景下开发的，后来自注意力网络中产生了无处不在的 transformer 架构。残差架构之所以取得成功，一种原因是与普通 DNN 相比具有更好的信号传播能力，其中信号传播指的是几何信息通过 DNN 层的传输，并由内核函数表示。
最近，使用信号传播原则来训练更深度的 DNN 并且残差架构中没有残差连接和 / 或归一化层的参与，成为了社区感兴趣的领域。原因有两个：首先验证了残差架构有效性的信号传播假设，从而阐明对 DNN 可解释性的理解；其次这可能会实现超越残差范式的 DNN 可训练性的一般原则和方法。
对于 CNN，Xiao et al. (2018)的工作表明，通过更好初始化提升的信号传播能够高效地训练普通深度网络，尽管与残差网络比速度显著降低。Martens et al. (2021) 的工作提出了 Deep Kernel Shaping (DKS)，使用激活函数转换来控制信号传播，使用 K-FAC 等强二阶优化器在 ImageNet 上实现了普通网络和残差网络的训练速度相等。Zhang et al. (2022) 的工作将 DKS 扩展到了更大类的激活函数，在泛化方面也实现了接近相等。
信号传播中需要分析的关键量是 DNN 的初始化时间内核，或者更准确地说，是无限宽度限制下的近似内核。对于多层感知机（MLP）以及使用 Delta 初始化的 CNN，该内核可以编写为仅包含 2D 函数的简单层递归，以便于进行直接分析。跨层 transformer 的内核演化更加复杂，因此 DKS 等现有方法不适用 transformer 或实际上任何包含自注意力层的架构。
在 MLP 中，信号传播是通过查看（一维）内核的行为来判断的，而 transformer 中的信号传播可以通过查看（高维）内核矩阵在网络层中的演化来判断。
该研究必须避免一种情况：对角线元素随深度增加快速增长或收缩，这与不受控制的激活范数有关，可能导致饱和损失或数值问题。避免秩崩溃（rank collapse）对于深度 transformer 的可训练性是必要的，而是否可以训练深度无残差 transformer 仍是一个悬而未决的问题。
ICLR 2023 盲审阶段的这篇论文解决了这个问题，首次证明了无需残差连接或归一化层时也可能成功训练深度 transformer。为此，他们研究了深度无残差 transformer 中的信号传播和秩崩溃问题，并推导出三种方法来阻止它们。具体而言，方法中使用了以下组合：参数初始化、偏置矩阵和位置相关的重缩放，并强调了 transformer 中信号传播特有的几种复杂性，包括与位置编码和因果掩蔽的交互。研究者实证证明了他们的方法可以生成可训练的深度无残差 transformer。
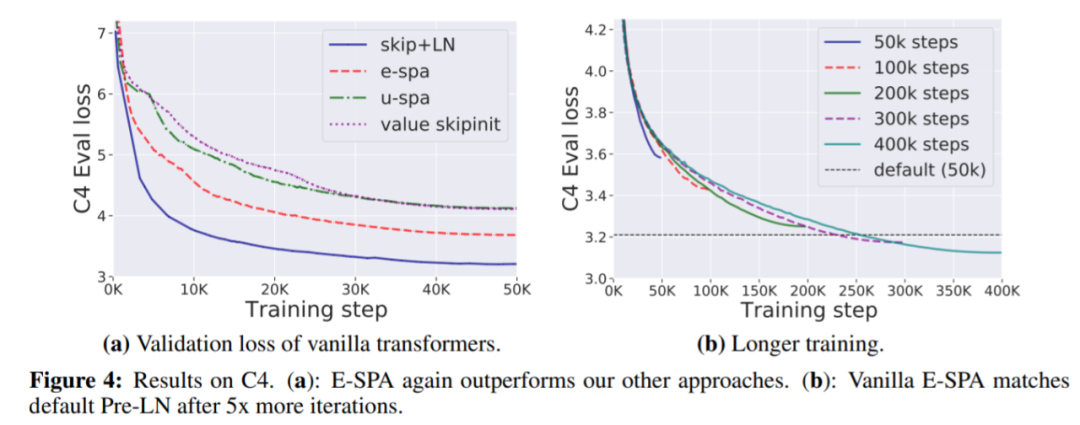
在实验部分，在 WikiText-103 和 C4 数据集上，研究者展示了使用他们主要的方法——指数信号保持注意力（Exponential Signal Preserving Attention, E-SPA），可以通过延长大约五倍的训练时间使得标准 transformer 与文中无残差 transformer 的训练损失相当。此外通过将这一方法与残差连接结合，研究者还表明无归一化层的 transformer 能够实现与标准 transformer 相当的训练速度。
论文地址：https://openreview.net/pdf?id=NPrsUQgMjKK
对于这篇论文，Google AI 首席工程师 Rohan Anil 认为是 Transformer 架构向前迈出的一大步，还是一个基础性的改进。
构造无捷径可训练的深层 Transformer
迄今为止，纠正 Transformer 秩崩溃（rank collapse）的唯一策略依赖于残差连接，该方式跳过了自注意力层固有的可训练性问题。与此相反，该研究直接解决这个问题。首先通过注意力层更好地理解信号传播，然后根据见解（insights）进行修改，以在深度 transformer 中实现对忠实信号的传输，无论是否使用残差连接，都可以对信号进行训练。
具体而言，首先，该研究对仅存在注意力的深度 vanilla transformer 进行了一下简单设置，之后他们假设该 transformer 具有单一头（h = 1）设置或具有多头设置，其中注意力矩阵 A 在不同头之间不会变化。如果块 l≤L 初始化时有注意力矩阵 A_l，则最终块的表示形式为 X_L：
对于上式而言，如果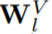
和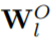
采用正交初始化，那么
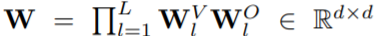就可以在初始化时正交。
在上述假设下，如果采用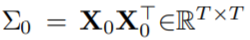
表示跨位置输入核矩阵，经过一些简化处理后，可以得到如下公式：
从这个简化公式（深度仅注意力 transformer 中的核矩阵）中，可以确定对 (A_l)_l 的三个要求：
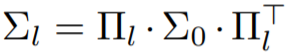必须在每个块中表现良好，避免退化情况，如秩崩溃和爆炸 / 消失的对角线值；- A_l 必须是元素非负 ∀l；
- A_l 应该是下三角∀l，以便与因果掩码注意力兼容。
在接下来的 3.1 和 3.2 节中，该研究专注于寻找满足上述需求的注意力矩阵，他们提出了 3 种方法 E-SPA、U-SPA 和 Value-Skipinit，每种方法都用来控制 transformer 的注意力矩阵，即使在很深的深度也能实现忠实的信号传播。此外，3.3 节演示了如何修改 softmax 注意力以实现这些注意力矩阵。
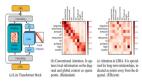
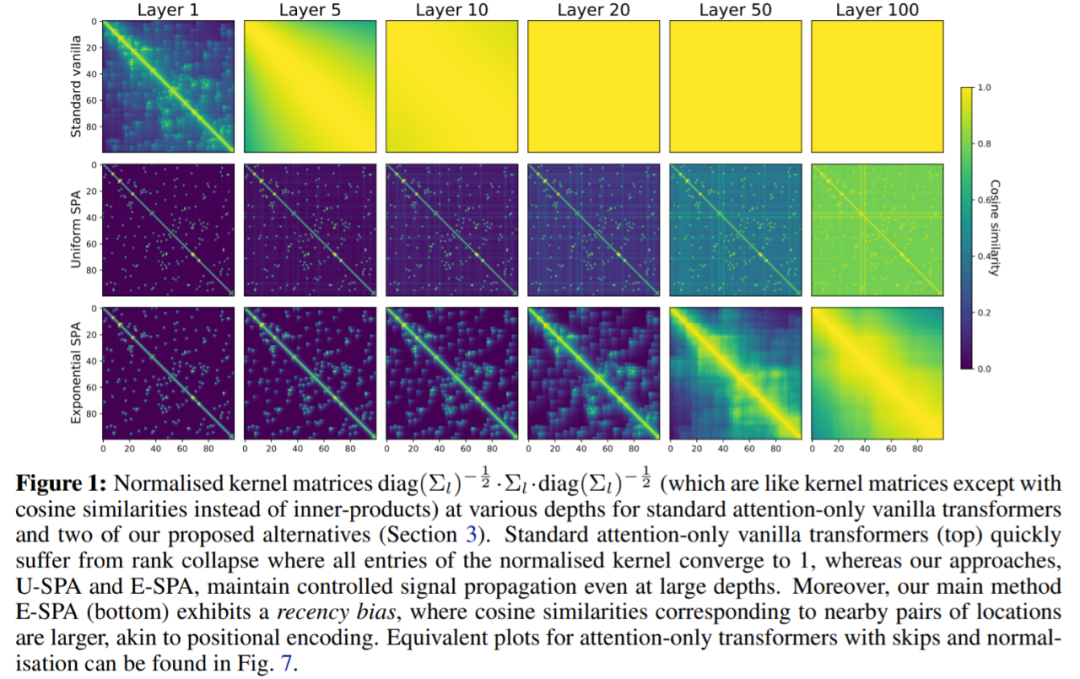
下图中，该研究对提出的两个 SPA 方案进行了验证，U-SPA 和 E-SPA，结果显示即使在网络较深时也能成功地避免仅注意力 vanilla transformers 中的秩崩溃现象。
实验
WikiText-103 基线：首先，该研究验证了没有残差连接的标准深度 transformer 是不可训练的，即使它们有归一化层 (LN) 和 transformed 激活，但本文的方法可以解决这个问题。如图 2 所示，可以清楚地看到，从标准 transformer 中移除残差连接使其不可训练，训练损失稳定在 7.5 左右。正如图 1 所示，标准 transformer 遭受了秩崩溃。
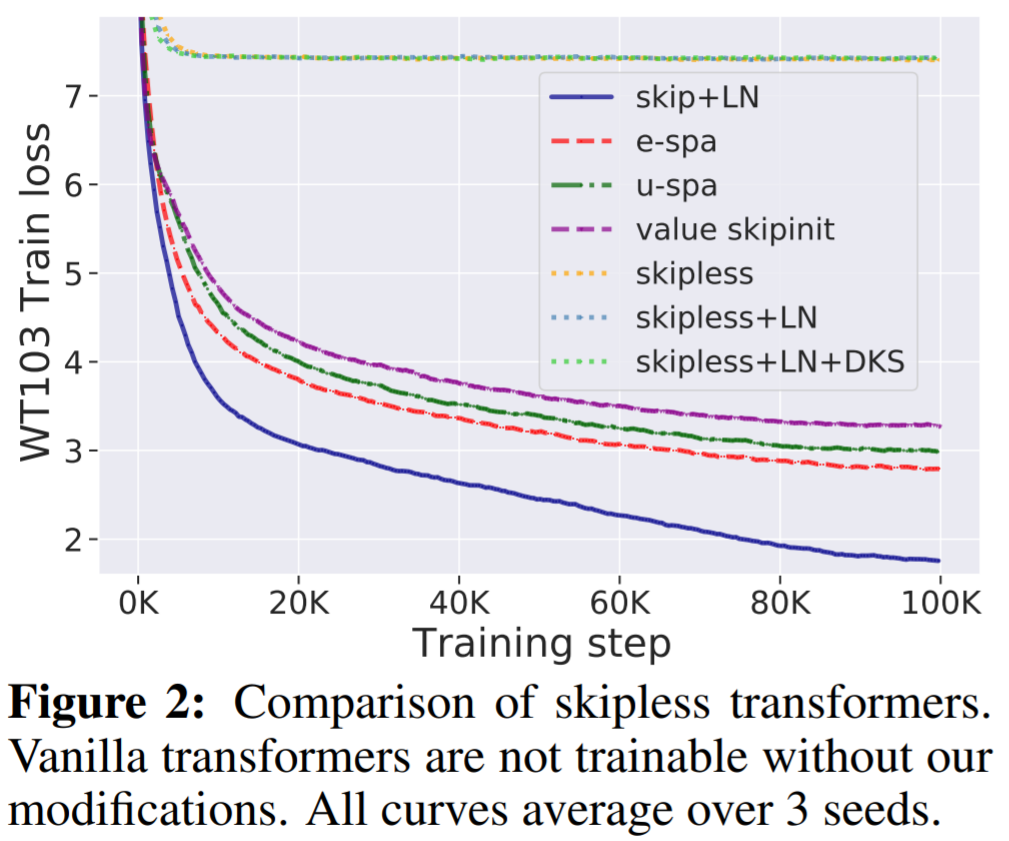
另一方面，该研究提出的 E-SPA 方法优于 U-SPA 和 Value-Skipinit。然而，与本文无残差方法相比，带有残差和 LN 的默认 transformer 仍然保持训练速度优势。
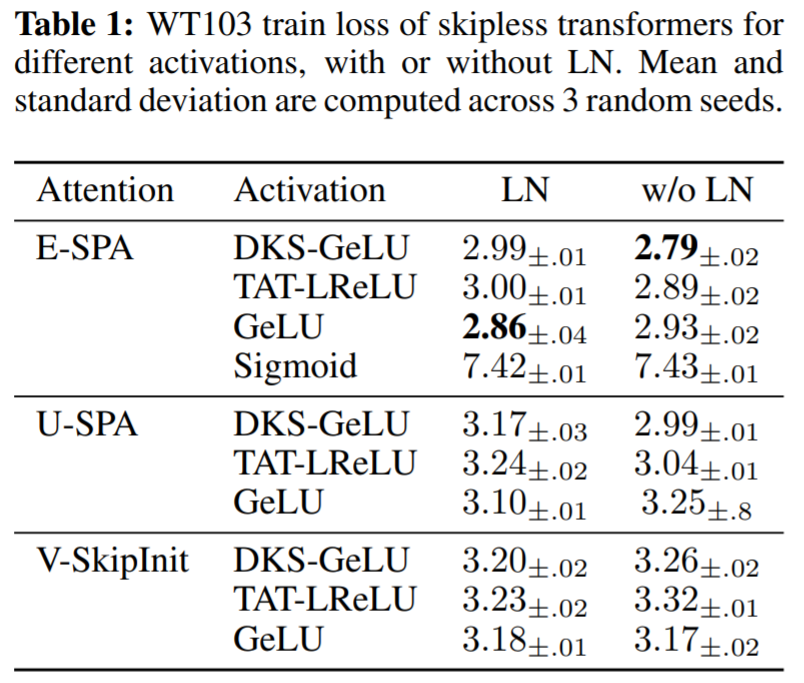
在表 1 中，该研究使用提出的方法评估了 MLP 块中不同激活函数的影响，以及 LN 在无残差 transformer 的使用。可以看到在深度为 36 处，本文方法针对一系列激活实现了良好的训练性能：DKS-transformed GeLU、TAT-transformed Leaky ReLU 以及 untransformed GeLU ，但不是 untransformed Sigmoid。通过实验还看到，层归一化对于训练速度而言相对不重要，甚至在使用 SPA 时对 transformed activation 的激活有害，因为 SPA 已经具有控制激活规范的内置机制。
在图 3 中，我们看到一种不需要更多迭代就能匹配默认 transformer 训练损失的方法是使用归一化残差连接。
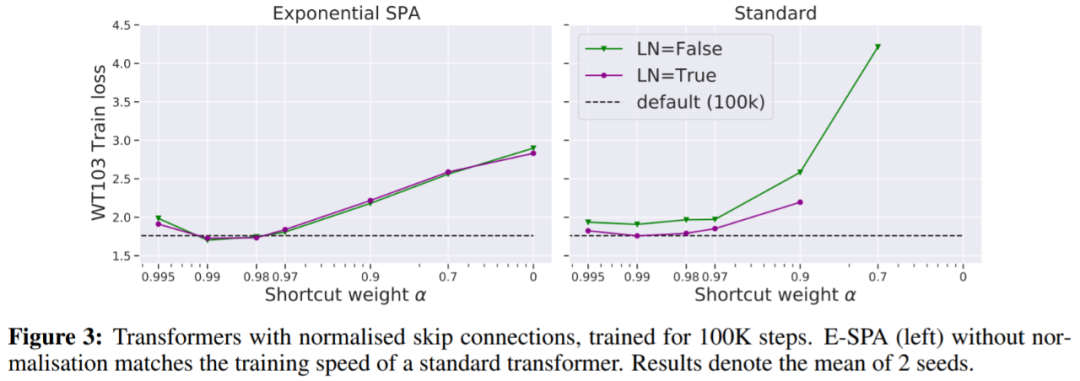
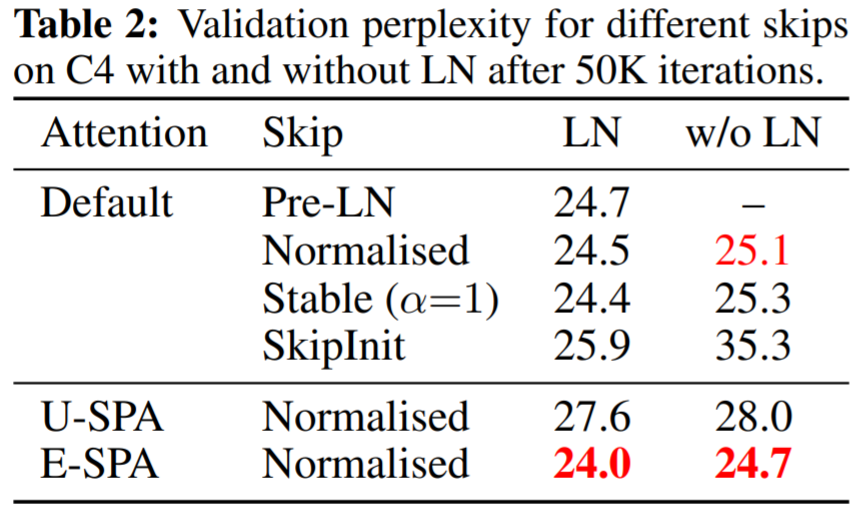
表 2 显示带有归一化残差和 LN 的 E-SPA 优于默认的 PreLN transformer。
下图 4(a)表明 E-SPA 再次优于其他方法；4(b)表明训练损失差距可以通过简单地增加训练时间来消除。
