如何使用 C++ 与 Python 实现二分查找-c++ 调用python

计算机科学中最基本的算法之一是二分查找算法。您可以使用两种方法实现二分查找：迭代方法和递归方法。虽然两种方法具有相同的时间复杂度，但迭代方法在空间复杂度方面要高效得多。

与递归方法产生的 O(logn) 相比，迭代方法的空间复杂度为 O(1) 。那么，如何使用 C、C++ 和 Python 中的迭代方法实现二分查找算法呢？

什么是二分查找？

二分查找也称为折半查找、对数查找或二分法，是一种搜索并返回排序数组中元素位置的算法。将搜索元素与中间元素进行比较。取下限和上限的平均值，您可以找到中间元素。

如果搜索元素大于中间元素，则意味着左侧的所有元素都小于搜索元素。因此，控件通过将下限增加到中间元素的下一个位置来移动到数组的右侧（如果数组按升序排列）。

同样，如果搜索元素小于中间元素，则意味着右侧的所有元素都大于搜索元素。因此，控件通过将上限更改为中间元素的先前位置来移动到数组的左侧。

与线性搜索实现相比，这大大减少了比较的数量，其中比较的数量等于最坏情况下的元素数量。事实证明，此方法对于查找电话簿中的数字或字典中的单词非常有用。

以下是二分查找算法的示意图：

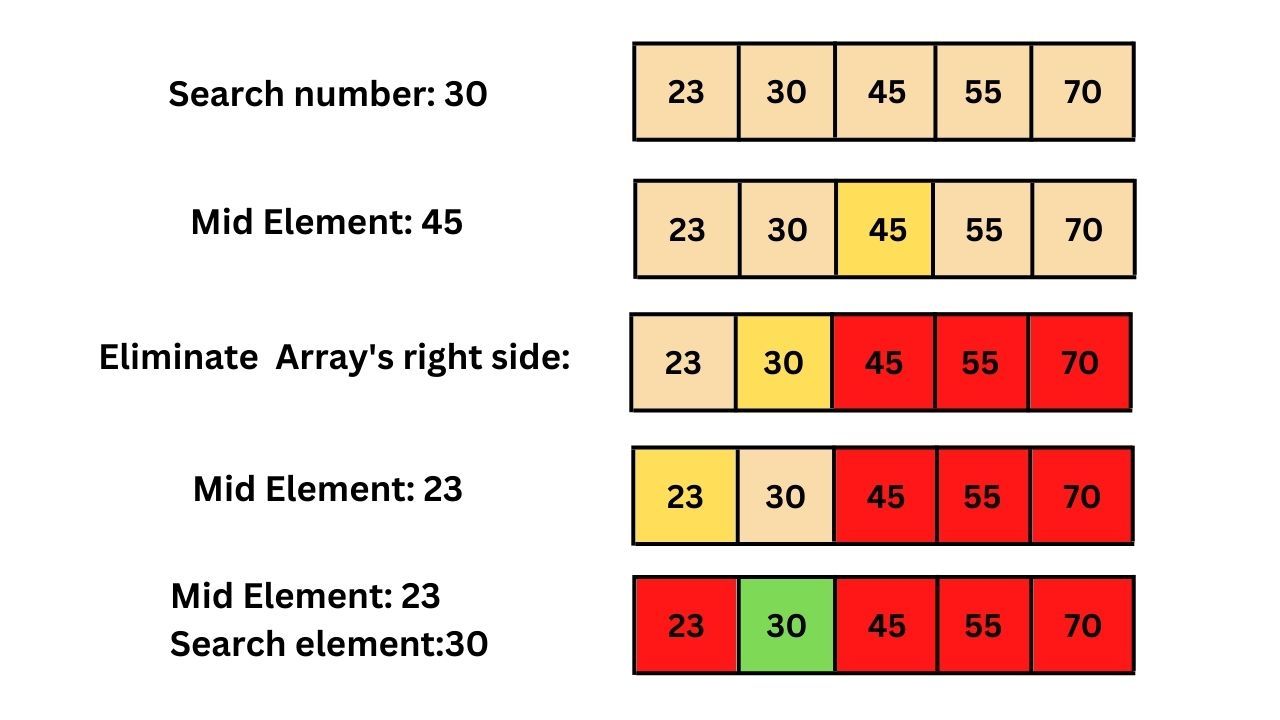
需要 C、C++ 和 Python 实现二分查找的完整源代码的请加微信：linuxgs。

使用 C 进行二分查找

请按照以下步骤使用 C 实现二分查找：

该程序定义了一个函数 binarySearch()，它返回找到的值的索引或 -1（如果它不存在）：

#include <stdio.h>

int binarySearch(int arr[], int arr_size, int search_number) {
/* ... */
}

该函数通过迭代缩小搜索空间来工作。由于二分查找适用于排序数组，因此您可以计算中间，否则没有意义。您可以要求用户提供排序数组，也可以使用排序算法（如气泡或选择排序）。

变量 low 和high 变量存储表示当前搜索空间边界的索引。mid 将索引存储在中间：

int low = 0, high = arr_size - 1, mid;

主 while() 循环将缩小搜索空间。如果 low索引的值大于 high 索引，则搜索空间已用尽，因此该值不存在。

while (low <= high) {
/* continues... [1] */
}

return -1;

更新循环开始时的中点后，有三种可能的结果：

如果 mid 的值是我们要查找的值，则返回该索引。
如果 mid 值大于我们要查找的值，请减小最大值。
如果 mid 值较小，则增加low 值。

/* [1] ...continued */
mid = (low + (high - low)) / 2;

if (arr[mid] == search_number)
return mid;
else if (arr[mid] > search_number)
high = mid - 1;
else
low = mid + 1;

使用用户输入测试函数。使用 scanf() 从命令行获取输入，包括数组大小、内容和要搜索的数字：

int main() {
int arr[100], i, arr_size, search_number;
printf("Enter number of elements: ");
scanf("%d", &arr_size);
printf("Please enter numbers: ");

for (i = 0; i < arr_size; i++) {
scanf("%d", &arr[i]);
}

printf("Enter number to be searched: ");
scanf("%d", &search_number);

i = binarySearch(arr, arr_size, search_number);

if (i==-1)
printf("Number not present");
else
printf("Number is present at position %d", i + 1);

return 0;
}

如果找到该数字，请显示其位置或索引，否则会显示一条消息，指出该数字不存在。

使用C++进行二分查找

可以通过导入输入输出流将 C 程序转换为C++程序，并使用命名空间 std 避免在整个程序中多次重复它。

#include <iostream>
using namespace std;

使用 cout 和提取运算符 << 而不是 printf() 和 cin 与插入运算符 >> 而不是 scanf()，你的 C++ 程序就准备好了。

printf("Enter number of elements: ");
cout << "Enter number of elements: ";

scanf("%d", &arr_size);
cin >> arr_size;

使用 Python 进行二分查找

由于 Python 没有对数组的内置支持，请使用列表。定义一个函数 binarySearch()，它接受三个参数、列表、大小和要搜索的数字：

def binarySearch(arr, arr_size, search_number):
low = 0
high = arr_size - 1
while low <= high:
mid = low + (high-low)//2
if arr[mid] == search_number:
return mid
elif arr[mid] > search_number:
high = mid - 1
else:
low = mid + 1
return -1

初始化两个变量，low 和 high，作为列表的下限和上限。与 C 实现类似，使用 while 循环来缩小搜索空间。初始化 mid 以存储列表的中间值。Python 提供了提供最大整数的除法运算符（//）。

进行比较并缩小搜索空间，直到中间值等于搜索编号。如果搜索编号不存在，控件将返回 -1。

arr_size = int(input("Enter number of elements: "))
arr=[]
print("Please enter numbers: ", end=" ")
for i in range(0,arr_size):
arr.append(int(input()))
search_number = int(input("Enter number to be searched: "))
result = binarySearch(arr, arr_size, search_number)

if result == -1:
print("Number not present")
else:
print("Number is present at position ", (result + 1))

使用用户输入测试函数。使用 input() 获取列表大小、其内容和要搜索的数字。使用 int() 将 Python 默认接受的字符串输入类型转换为整数。要将数字添加到列表中，请使用 append() 函数。

调用 binarySearch() 并传递参数。如果找到该数字，请显示其位置或索引，否则会显示一条消息，指出该数字不存在 Number not present。

二分查找算法的输出

以下是数组中存在元素时二分查找算法的输出：

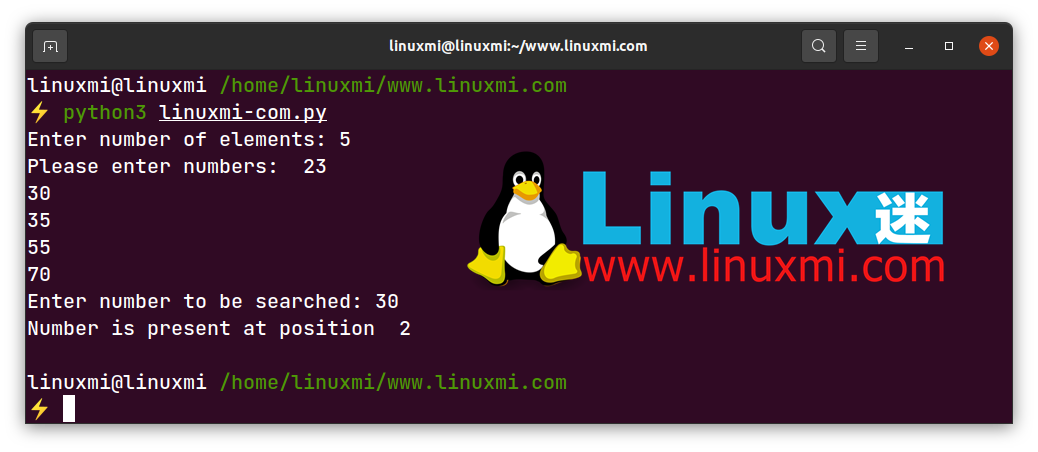
以下是数组中不存在元素时二分查找算法的输出：

学习基本数据结构和算法

搜索是您学习的第一批算法之一，在编码竞赛、实习和面试中经常被问到。您应该学习的其他一些算法是排序、哈希、动态规划、字符串匹配和素数测试算法。

此外，了解算法的时间和空间复杂性至关重要。它们是计算机科学中确定任何算法效率的最关键概念之一。有了数据结构和算法的知识，你一定会构建最好的程序。