「在一个带权有向图G=(V,E)中，每条边的权是一个实数。另外，还给定V中的一个顶点，称为源。
计算从源到其他所有各顶点的最短路径长度，这就是单源最短路径（SSSP）问题。」
半个多世纪以来，世界各地的研究人员一直在努力解决这个问题。而现在，该算法谜题终于被哥本哈根大学计算机科学系的研究团队成功解决。
负权值SSSP算法：速度快、效率高
论文链接：https://arxiv.org/abs/2203.03456
接受采访时，研究人员Christian Wulff-Nilsen称，他们的解决方案是第一个突破存在30多年的Õ(n(4/3) log W)运算时间约束的，带有负权值的SSSP组合算法。
关于SSSP有两个经典算法：Dijkstra算法（迪克斯特拉算法）和Bellman-Ford算法（贝尔曼-福特算法），两者都有各自的局限性。
Dijkstra算法运算时间最短，能达到近线性时间 O(m + n log n) ，但不能计算负权值边。
Bellman-Ford算法可以计算负权值边，但运算时间过长，达到O(mn)。目前，最顶尖的解决负权边的SSSP算法都依赖于复杂的连续优化和动态代数和图形算法。这就导致即使后世学者不断优化该算法，其运算时间仍需Õ(n(4/3) log W)。这个运算时间的约束已经存在三十年之久。
面对这些局限，Wulff-Nilsen提出了两个问题：
1）带负权边算法的运算能否达到近线性时间？
2）能否用简单的工具达到这个目的？
有没有一种方法，可以既要时间，又要质量呢？
别说，还真有。
Wulff-Nilsen提出的算法为图像缩放算法，被简易图像分解算法Low Diameter Decomposition强化。通常情况，该分解算法只用于非负权边的图形分解，而该研究的贡献之一就在于将其运用到负权边图像中，加强负权边SSSP递归缩放算法。
推导过程
Wulff-Nilsen以Johnson的价格算法为基础。提出：在图像G = (V, E, w)中，令Φ为任意函数：V→Z。令w(Φ)为权函数：
定义：，则：。在图像G = (V, E,w)和图像G' = (V, E,w')中，若：1）图像G中的最短距离与图像G’中的最短距离相等，反之亦然；2）G只在G'含有负权环时含有负权环，则图像G与图像G'相等。
推论2.7考虑到任意图像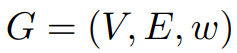
和价格函数Φ。在 u, v ∈ V 中，
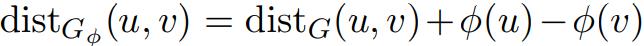。而在任意环C中，
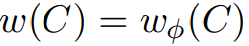。因此，G和
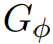相等。如果
，
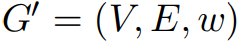
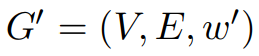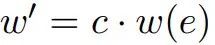，那么G和G'相等。
该算法的目的是在计算价格函数Φ时，在GΦ中的所有边权都为非负，假设不存在负权环。之后就可以在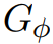
上运行Dijkstra算法。
之后，Wulff-Nilsen开始介绍自己的算法框架。
首先，Wulff-Nilsen假设存在一种算法 Dijkstra（G,s），输入无负权边的图形G，顶点s ∈ V，G中的s输出最短路径树。运行时间为O(m + n log n)。
如果G是一个DAG（有向无环图），计算一个价格函数Φ，使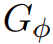
具有非负权边是很简单的：只需在拓扑的v1, ..., vn上循环，并设置Φ(vi)，使所有进入的边权值为非负。
单源最短路径问题的目的是找到从给定起始节点到网络中所有其他节点的最短路径。
网络表示为由节点和它们之间的连接组成的图形，称为边。
每条边都有一个方向（例如，这可用于表示单向道路）以及一个权重，用于表示沿该边行驶的成本。如果所有边权重都是非负的，则可以使用经典的Dijkstra算法在几乎线性的时间内解决问题。
新结果在与Dijkstra算法几乎相同的时间内解决了这个问题，但也允许负边权重。
之后，Wulff-Nilsen提到了组合工具中最重要的两个算法：ScaleDown和SPmain。
ScaleDown算法分阶段运行，在最后一个阶段它用ElimNeg（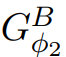
）来计算价格函数Φ2。如果ElimNeg终止，它将返回价格函数ψ′，让
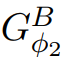所有边值非负；换句话说，因为
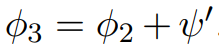，所以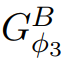
中不包含负权值。
这意味着，对于所有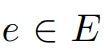
，
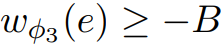都满足条件（因为
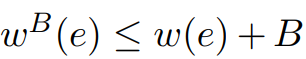）。由此证明了 ScaleDown输出的正确性。
如果算法终止，则对于所有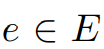
和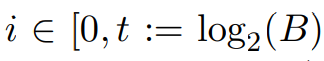
，
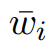是积分，并且对于所有
，
。
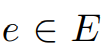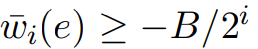这意味着对于所有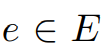
，
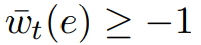。因此图形G*具有非负权值。
通过归纳法，假设该理论适用于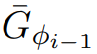
，算法第5行中对ScaleDown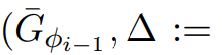
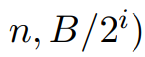的调用满足必要的输入属性。
因此，通过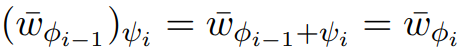
和ScaleDown的Output，可以得到
。
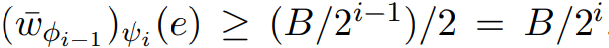由于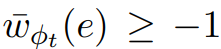
，若令C为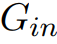
中任意负权环，由于
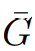中的所有权值都为2n的倍数，且
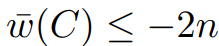；又知
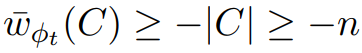，故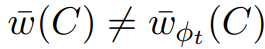
与推论2.7不符。
从而得出结论：如果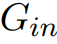
包含负权环，则算法不会终止。
由此可以证明，SPmain算法的正确性。
至此，Wulff-Nilsen的负权值SSSP解决方案中最重要的两个算法均证明成立。新算法在保证近线性时间的同时，成功引入了负权值。
60年后，寻求答案不仅为了解谜
去年，Wulff-Nilsen在同一领域取得了另一项突破，结果涉及如何在随时间变化的网络中找到最短路径。他对最近谜语的解决方案建立在这项工作的基础上。
他认为，解决SSSP问题可以为算法铺平道路，不仅可以帮助电动汽车立即计算到达目的地的最快路线，而且能保证以最节能的方式做到这一点。
Wulff-Nilsen解释道：“我们的算法里加入了负权这个以前算法没有的维度。一个实际的例子是在山间驾驶时，有了负权这一维度，导航系统可以为电动车车主推荐下坡路多的路线，使电动车可以在下坡时进行充电。”
Wulff-Nilsen还表示，他们的算法不仅可以用于电动车路线规划，还能用于监测金融业的投机行为。他说：“原则上，该算法可以用来为中央银行等用户预警，警告投机者在投机买卖各种货币。现在，很多不法之徒利用计算机犯罪，但由于我们的算法如此之快，或许能够被用来监测，在人们利用漏洞之前及时发现。”
1959年，当Dijkstra首次提出最短距离问题时，可能他也不会想到，60多年来，一直有人不断优化这一问题的方案。或许也会惊讶，谜题的答案竟然有如此丰富的内涵。
或许，这就是科学的魅力吧。
