自回归滞后模型进行多变量时间序列预测-多变量时间序列模型

下图显示了关于不同类型葡萄酒销量的月度多元时间序列。每种葡萄酒类型都是时间序列中的一个变量。

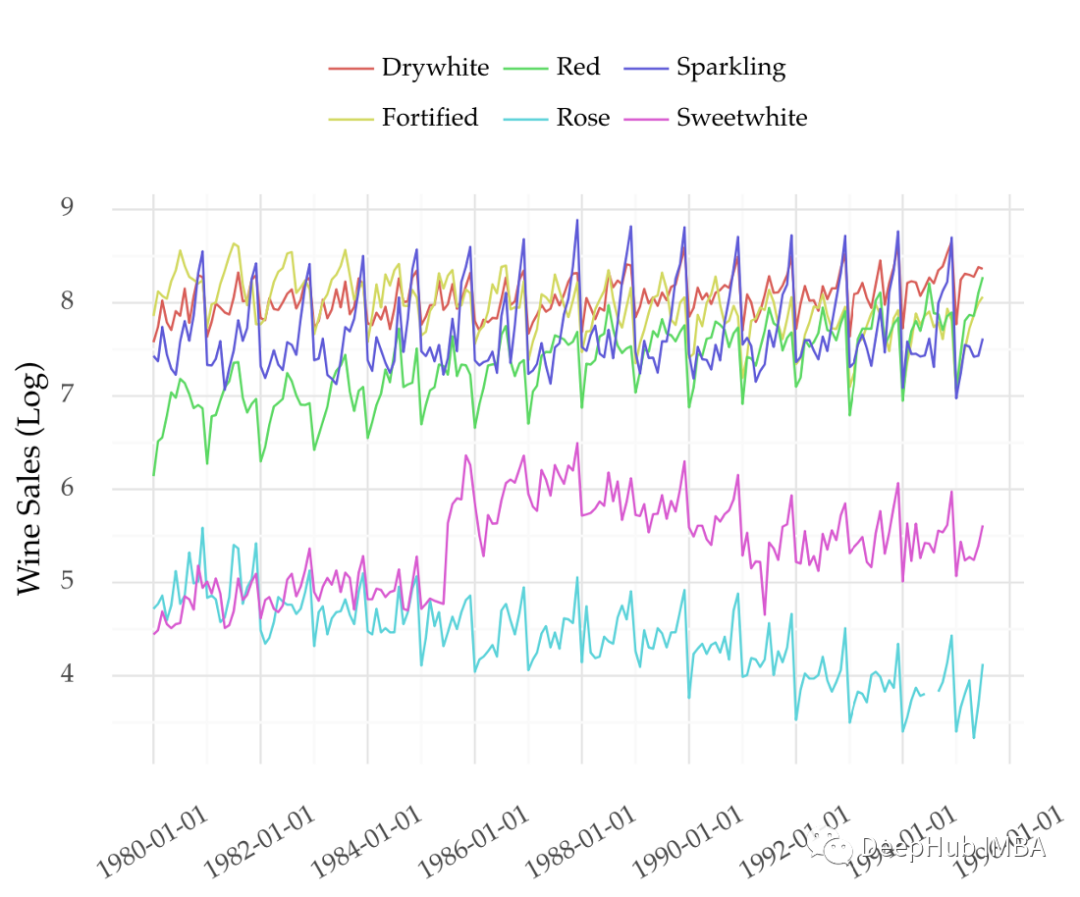
假设要预测其中一个变量。比如，sparkling wine。如何建立一个模型来进行预测呢？

一种常见的方法是将该变量其视为单变量时间序列。这样就有很多方法可以用来模拟这些系列。比如 ARIMA、指数平滑或 Facebook 的 Prophet，还有自回归的机器学习方法也可以使用。

但是其他变量可能包含sparkling wine未来销售的重要线索。看看下面的相关矩阵。

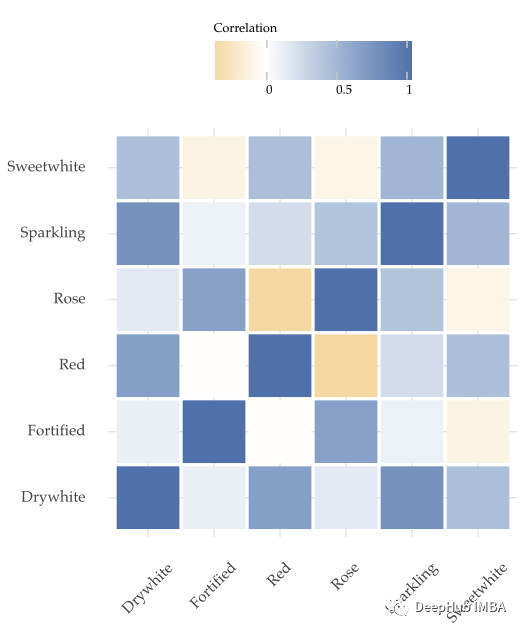
可以看到sparkling wine的销量(第二排)与其他葡萄酒的销量有相当的相关性。所以在模型中包含这些变量可能是一个好主意。

本文将介绍可以通过一种称为自回归分布滞后(ARDL)的方法来做到这一点。

Auto-Regressive Distributed Lag

ARDL模型采用自回归。自回归是大多数单变量时间序列模型的基础。它主要分为两个步骤。

首先将(单变量)时间序列从一个值序列转换为一个矩阵。可以用用延时嵌入法（time delay embedding）来做到这一点。尽管名字很花哨，但这种方法非常简单。它基于之前的最近值对每个值进行建模。然后建立一个回归模型。未来值表示目标变量。解释变量是过去最近的值。

多元时间序列的思路与此类似，我们可以将其他变量的过去值添加到解释变量中。这就是了被称为自回归分布式滞后方法。分布式滞后的意思指的是使用额外变量的滞后。

现在我们把他们进行整合，时间序列中一个变量的未来值取决于它自身的滞后值以及其他变量的滞后值。

代码实现

多变量时间序列通常是指许多相关产品的销售数据。我们这里以葡萄酒销售时间序列为例。当然ARDL方法也适用于零售以外的其他领域。

转换时间序列

首先使用下面的脚本转换时间序列。

import pandas as pd
 
 # https://github.com/vcerqueira/blog/
 from src.tde import time_delay_embedding
 
 wine = pd.read_csv('data/wine_sales.csv', parse_dates=['date'])
 
 # setting date as index
 wine.set_index('date', inplace=True)
 
 # you can simulate some data with the following code
 # wine = pd.DataFrame(np.random.random((100, 6)),
 #           columns=['Fortified','Drywhite','Sweetwhite',
 #                     'Red','Rose','Sparkling'])
 
 # create data set with lagged features using time delay embedding
 wine_ds = []
 for col in wine:
  
  
 
 # concatenating all variables
 wine_df = pd.concat(wine_ds, axis=1).dropna()
 
 # defining target (Y) and explanatory variables (X)
 predictor_variables = wine_df.columns.str.contains('\(t\-')
 target_variables = wine_df.columns.str.contains('Sparkling\(t\+')
 
 X = wine_df.iloc[:, predictor_variables]
 Y = wine_df.iloc[:, target_variables]

将 time_delay_embedding 函数应用于时间序列中的每个变量（第 18-22 行）。第 23 行将结果与我们的数据集进行合并。

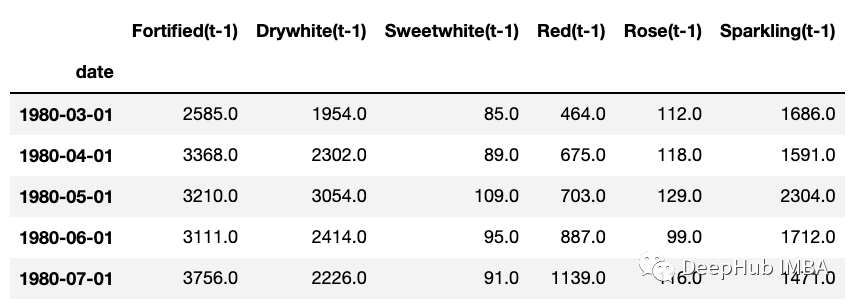
解释变量 (X) 是每个变量在每个时间步长的最后 12 个已知值（第 29 行）。以下是它们如何查找滞后 t-1（为简洁起见省略了其他滞后值）：

目标变量在第30行中定义。这指的是未来销售的6个值:

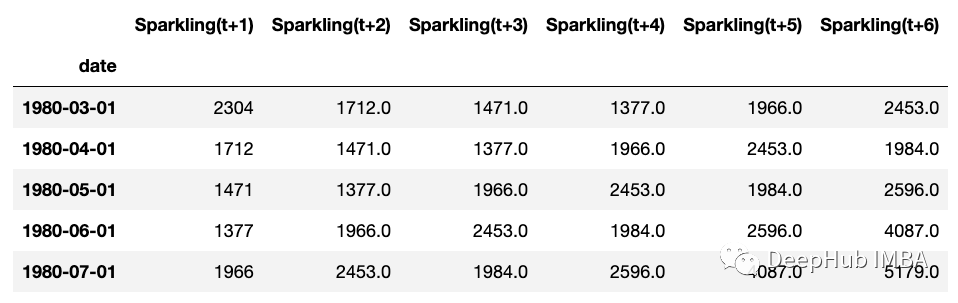
建立模型

准备好数据之后，就可以构建模型了。使用随机森林进行一个简单的训练和测试循环。

from sklearn.model_selection import train_test_split
 from sklearn.metrics import mean_absolute_error as mae
 from sklearn.ensemble import RandomForestRegressor
 
 
 # train/test split
 X_tr, X_ts, Y_tr, Y_ts = train_test_split(X, Y, test_size=0.3, shuffle=False)
 
 # fitting a RF model
 model = RandomForestRegressor()
 model.fit(X_tr, Y_tr)
 
 # getting forecasts for the test set
 preds = model.predict(X_ts)
 
 # computing MAE error
 print(mae(Y_ts, preds))
 # 288.13

拟合模型之后(第11行)，得到了测试集中的预测(第14行)。该模型的平均绝对误差为288.13。

滞后参数的选择

上面的基线使用每个变量的 12 个滞后作为解释变量。这是在函数 time_delay_embedding 的参数 n_lags 中定义的。那么应该如何设置这个参数的值呢？

很难先验地说应该包括多少值，因为这取决于输入数据和特定变量。

解决这个问题的一种简单方法是使用特征选择。从相当数量的值开始，然后根据重要性评分或预测性能来修改这个数字，或者直接使用GridSearch进行超参数的搜索。

我们这里将简单的演示一个判断的过程：根据随机森林的重要性得分选择前 10 个特征。

# getting importance scores from previous model
 importance_scores = pd.Series(dict(zip(X_tr.columns, model.feature_importances_)))
 
 # getting top 10 features
 top_10_features = importance_scores.sort_values(ascending=False)[:10]
 top_10_features_nm = top_10_features.index
 
 X_tr_top = X_tr[top_10_features_nm]
 X_ts_top = X_ts[top_10_features_nm]
 
 # re-fitting the model
 model_top_features = RandomForestRegressor()
 model_top_features.fit(X_tr_top, Y_tr)
 
 # getting forecasts for the test set
 preds_topf = model_top_features.predict(X_ts_top)
 
 # computing MAE error
 print(mae(Y_ts, preds_topf))
 # 274.36

前10个特征比原始预测显示出更好的预测性能。以下是这些功能的重要性:

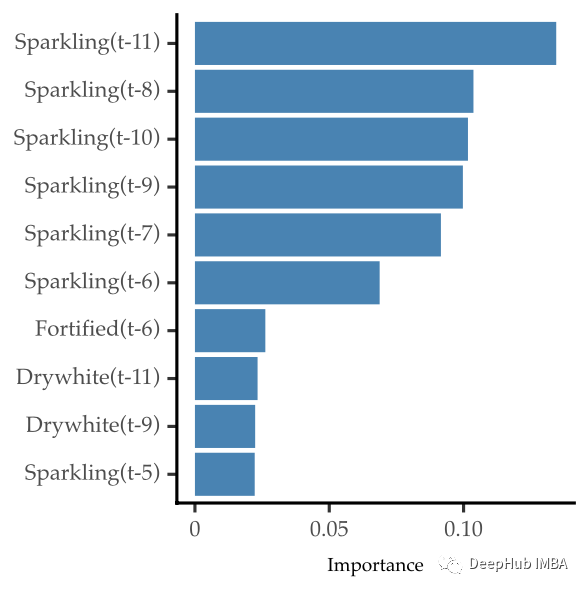
目标变量(Sparkling)的滞后是最重要的。但是其他变量的一些滞后也是相关的。

ARDL 的扩展

多个目标变量预测，目前为止，我们都在预测单个变量（sparkling wine）。如果我们想要同时预测几个变量呢？

这种方法被称为：向量自回归 (VAR)

就像在 ARDL 中一样，每个变量都是根据其滞后和其他变量的滞后建模的。当想要预测多个变量而不仅仅是一个变量时，将使用 VAR。

与全局预测模型的关系

值得注意的是，ARDL并不等同于全局预测模型（Global Forecasting Models）。

在ARDL的前提下，每个变量的信息被添加到解释变量中。变量的数量通常很少，且大小相同。

全局预测模型汇集了许多时间序列的历史观测结果。模型通过这些所有观察结果进行建模。每一个新的时间序列都是作为新的观察结果加入到数据中。全局预测模型通常涉及多达数千个时间序列量级也很大。

总结

本文的主要内容如下：多变量时间序列包含两个或多个变量；ARDL 方法可用于多变量时间序列的监督学习；使用特征选择策略优化滞后数。如果要预测多个变量，可以使用 VAR 方法。

最后本文的数据集在这里：

https://rdrr.io/cran/Rssa/man/AustralianWine.html