
上周面试一个候选人,问了一个数据结构与算法的问题,表达式求值。
题目大概是这样的:
- 输入长度为n的字符串,例如:1+2+3*4*5
- 输出表达式的值,即:63
我暗示的问:应该用什么数据结构?候选人回答:栈。
画外音:算是答对。
问:时间复杂度呢?回答:O(n^2)
画外音:额,应该不需要两个for循环吧。
我接着提示:应该先计算哪一步?候选人回答:先计算3*4。
画外音:额,难道是乘除大于加减?
实际应该先计算1+2,说明候选人对“表达式求值”并没有搞透。
怎么用栈来实现呢?候选人:…
本来以为是送分题,候选人竟一时语塞。
为了广大面试的同学不再在这一题上送命,今天花几分钟把这个问题讲透彻。
画外音:希望没有帮面试官增加题库。
“表达式求值”问题,两个核心关键点:
(1) 双栈,一个操作数栈,一个运算符栈;
(2) 运算符优先级,栈顶运算符,和,即将入栈的运算符的优先级比较:
- 如果栈顶的运算符优先级低,新运算符直接入栈
- 如果栈顶的运算符优先级高,先出栈计算,新运算符再入栈
仍以1+2+3*4*5举例,看是如何利用上述两个关键点实施计算的。
首先,这个例子只有+和*两个运算符,所以它的运算符表是:

这里的含义是:
- 如果栈顶是+,即将入栈的是+,栈顶优先级高,需要先计算,再入栈;
- 如果栈顶是+,即将入栈的是*,栈顶优先级低,直接入栈;
- 如果栈顶是*,即将入栈的是+,栈顶优先级高,需要先计算,再入栈;
- 如果栈顶是*,即将入栈的是*,栈顶优先级高,需要先计算,再入栈;
画外音:运算符有+-*/()~^&都没问题,如果共有n个运算符,会有一个n*n的优先级表。
有了运算符表,一切就好办了。
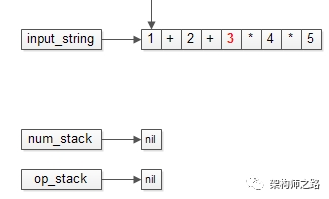
一开始,初始化好输入的字符串,以及操作数栈,运算符栈。
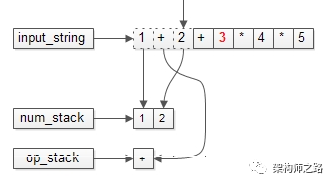
一步步,扫描字符串,操作数一个个入栈,运算符也入栈。
画外音:如果有“789”这样的多个字符的多位数,要先转化为数字789,这个过程很容易。
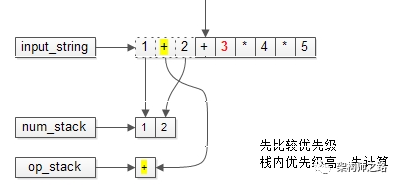
下一个操作符要入栈时,需要先比较优先级。
栈内的优先级高,必须先计算,才能入栈。
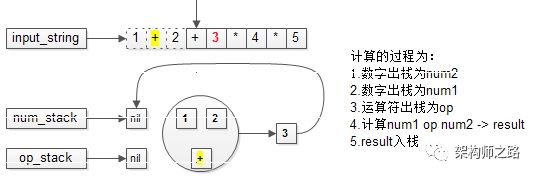
计算的过程为:
- 操作数出栈,作为num2;
- 操作数出栈,作为num1;
- 运算符出栈,作为op;
- 计算出结果;
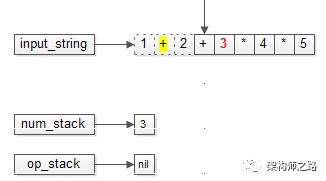
(5) 结果入操作数栈;
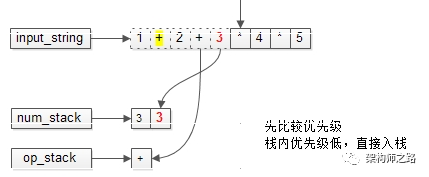
接下来,运算符和操作数才能继续入栈。下一个操作符要入栈时,继续比较与栈顶的优先级。
栈内的优先级低,可以直接入栈。
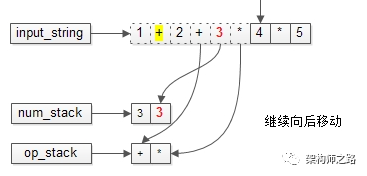
字符串继续移动。
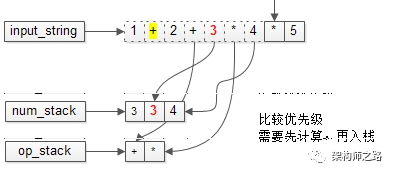
又要比较优先级了。
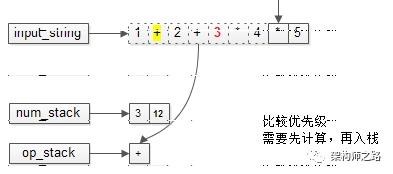
栈内的优先级高,还是先计算(3*4=12),再入栈。
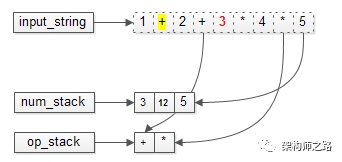
不断入栈,直到字符串扫描完毕。
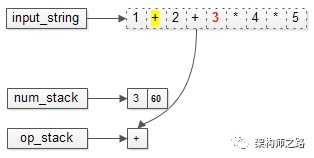
不断出栈,直到得到最终结果3+60=63,算法完成。
总结
“表达式求值”问题,两个核心关键点:
(1) 双栈,一个操作数栈,一个运算符栈;
(2) 运算符优先级,栈顶运算符,和,即将入栈的运算符的优先级比较:
- 如果栈顶的运算符优先级低,新运算符直接入栈
- 如果栈顶的运算符优先级高,先出栈计算,新运算符再入栈
这个方法的时间复杂度为O(n),整个字符串只需要扫描一遍。
思路比结论重要,学到了吗?



























