人类在成长过程的不同阶段均需要掌握很多的知识点来求解大量的数学题。然而,知识点看懂了不算真的懂,能求解题目才能体现人类的智慧。近年来,神经网络在计算机视觉,模式匹配、自然语言处理、强化学习等领域取得了巨大成功,但神经网络模型的离散组合推理能力远不及人类。那么,神经网络能否理解数学题,并解出这些题目呢?如果可以,那么神经网络的解题能力如何?
从数据形式上来说,一道数学题可以看作是一个序列,而其解答(解题步骤或者求解表达式)往往也是以序列的形式呈现。那么数学题求解可以看作是从自然语言到数学语言的翻译问题,神经网络模型从形式上能求解数学问题。从前人的各种研究工作中可以获知,神经网络能在翻译问题上获得很好的性能,并在多个数据集上获得了超越了人类的性能。然而,与机器翻译显著不同,除了题目语义理解能力之外,数学题求解往往还需要模型具备对代数泛化对象和实体的离散组合推理能力。
为了探究深度模型对数学题的解题能力,中山大学人机物智能融合实验室在前人研究的基础上以中小学数学应用题和几何计算题为切入点,开展了一系列研究,改进了深度模型的语义理解、认知推理和数学解题能力。本文将对中山大学人机物智能融合实验室在数学解题领域的一系列研究进行简要介绍。
论文1:Semantically-Aligned Universal Tree-Structured Solver for Math Word Problems

The 2020 Conference on Empirical Methods in Natural Language Processing
论文地址:https://aclanthology.org/2020.emnlp-main.309.pdf
一个实用的数学应用题求解器应该能够解决各种类型的数学应用题,如一元一次方程,二元一次方程组,一元二次方程等类型。然而,大多数的数学应用题求解工作只针对四则运算类题目进行设计,而这类设计往往难以扩展到更多题型,无法使用一个统一的数学应用题求解器同时求解各种类型表达式的应用题。此外,当下的大部分数学应用题求解器缺乏对题目文本和求解表达式之间的语义约束。
针对上述问题,中山大学人机物智能融合实验室团队提出一种统一表达式树表示方案,通过引入额外的运算符连结多个表达式,将一元一次方程,二元一次方程组,一元二次方程等类型的表达式进行统一表示,从而可以简化求解器的设计的同时也可以求解多种类型的应用题,如图 1 所示。
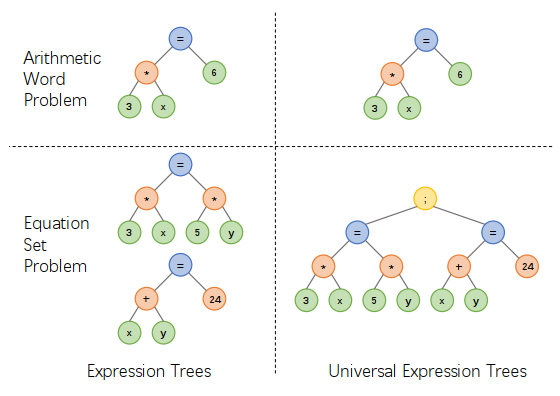
图 1 统一表达式树表示方案设计
基于统一表达式树表示方案,我们进而提出了一种语义对齐的树结构通用求解器(SAU-Solver),如图 2 所示。我们的树结构通用求解器由两部分组成,基于双层 GRU 的问题编码器和基于统一表达式树表示的树结构解码器。并且在训练过程中,我们引入了语义对齐正则化,通过约束表达式子树与题目上下文的一致性使得我们的通用求解器能更充分地考虑问题和表达式之间的语义关系,发掘各类数学知识,从而提升求解器的表达式生成能力。
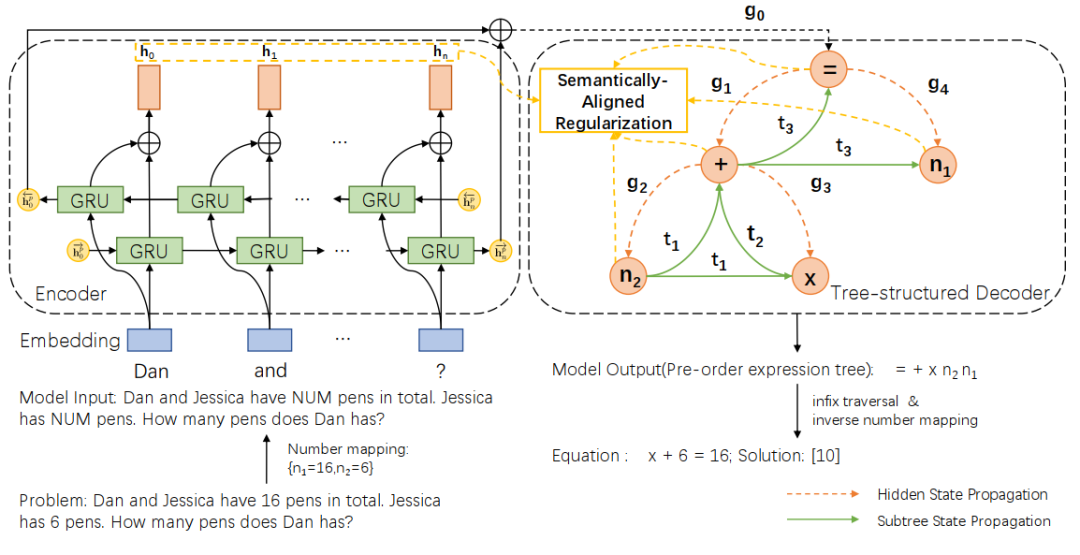
图 2 语义对齐树结构求解器
此外,为了更好地衡量求解器的通用性和求解能力,我们还针对当前标注数据集中题型种类单一的问题,构建了一个中等规模的多题型数据集 HMWP,该数据集包括了求解表达式为一元一次方程,二元一次方程组,一元二次方程等多种表达式类型的数千道数学文字题目。我们的实验表明,具有多题型的数据集比种类单一的数据集对求解器来说更具有挑战性,也能更好地衡量求解器的解题能力,推动求解器社区的研究。
在实验中,文章将提出的 SAU-Solver 与现有方法在 HMWP、Math23K、ALG514 和 Dolphin18K-Manual 进行了对比。实验结果如下图所示,证明了我们方法的通用性和更好的数学解题能力。
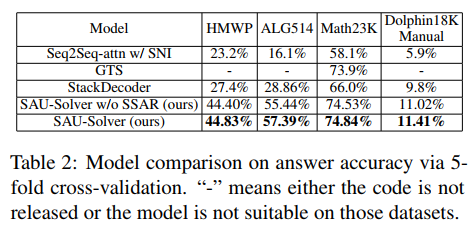
更多研究细节,可参考原论文。
论文2:Neural-Symbolic Solver for Math Word Problems with Auxiliary Tasks

The 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing
论文地址:https://arxiv.org/abs/2107.01431
当前的初等数学应用题求解器没有考虑各种数学符号约束,而是仅是简单地使用编码器 - 解码器框架进行求解的问题,从而导致了不合理的预测。而引入符号约束和符号推理对于数学应用题自动求解是非常关键的。
因此,中山大学人机物智能融合实验室团队引入神经 - 符号计算范式,提出新型的神经 - 符号求解器(NS-Solver),以辅助任务的方式进行显式的知识注入,从而实现不同层级的符号约束。其技术架构如图 3 所示。NS-Solver 在网络骨干上由三个组件构建:1)Problem Reader,通过双层双向 GRU 网络对数学题进行高效的语义理解和表示;2)Programmer,负责基于问题语义以及常识预测结果进行符号推理,生成求解表达式。3)Executor,利用 sympy 库进行表达式求解,获取最终答案。
在符号约束上,我们提出多种辅助任务来利用额外的训练信号和利用常识预测结果来显式地约束符号表,降低问题求解搜索空间:1)自监督的数字预测任务:通过预测题目中数字的位置和数量来更好地理解题目语义;2)常识量词预测任务:注入常识知识并利用预测结果约束符号表,降低搜索空间;3)一致性检查:从语义层面检查解题器的输出与目标表达式的一致性;4)对偶利用任务:通过问题到表达式和表达式到问题的双向约束,强化解题器的问题语义理解。
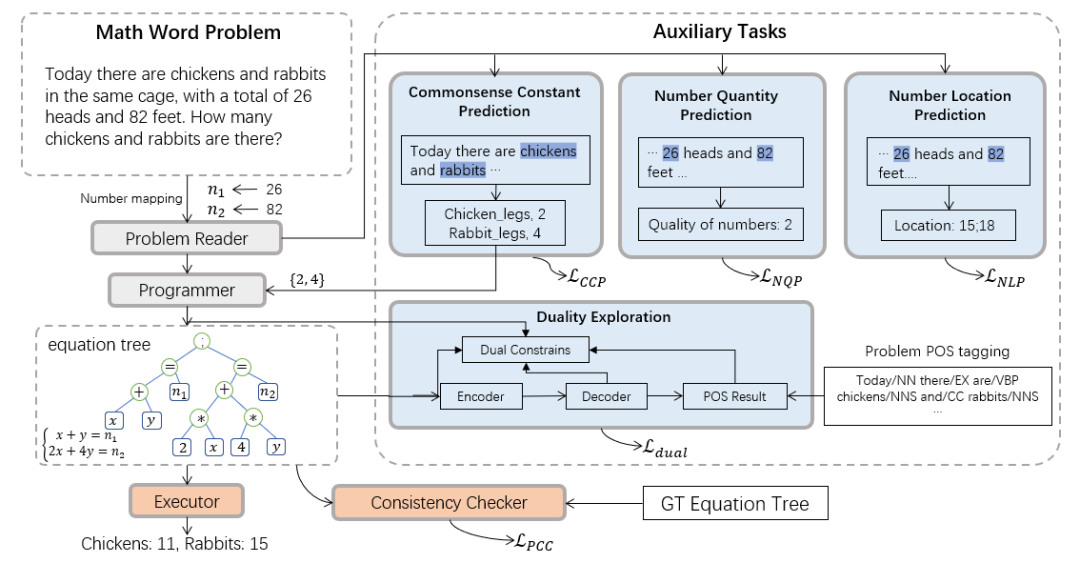
图 3 神经 - 符号求解器(NS-Solver)
此外,为了更好地验证求解器的性能,我们还构建了一个更大规模的多题型数学应用题数据集 CM17K,从而更好地推动数学解题社区的研究。CM17K 包含了 6215 道四则运算类应用题,5193 道一元一次方程类应用题,3129 道一元非线性方程类应用题和 2498 道方程组类应用题。CM17K 和 Math23K 的数据统计如下表所示。从数据统计上可以看出,CM17K 相比 Math23K 具有更长的题目信息,更长的求解表达式,涉及更多的常识等,这意味着 CM17K 在求解难度上更好地刻画解题器的性能。
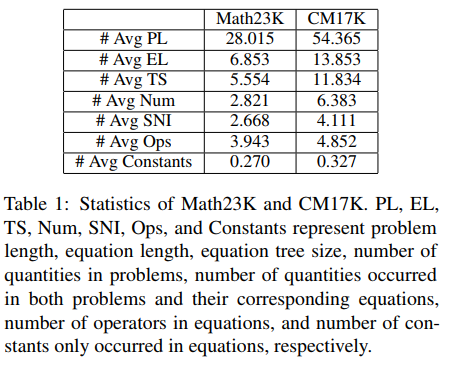
在实验中,文章将提出的 NS-Solver 与现有方法在 Math23K 和 CM17K 上进行了对比,并进行了消融实验,证明了 NS-Solver 良好的解题能力和通用性。其实验结果如下面两个表所示。
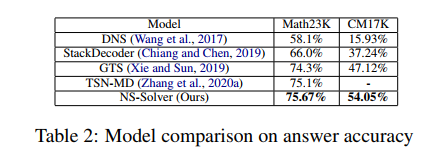
此外,我们还对辅助任务进行了消融实验,如下图所示。实验结果证明了各个辅助任务均能提升 NS-Solver 的解题能力。
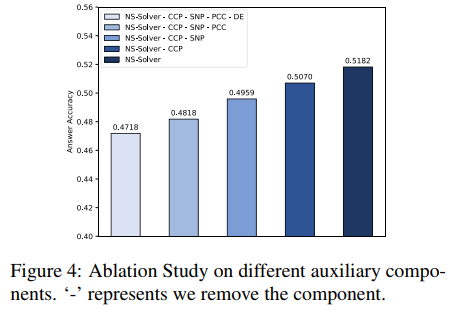
更多研究细节,可参考原论文。
论文3:GeoQA – A Geometric Question Answering Benchmark Towards Multimodal Numerical Reasoning

Findings of the Association for Computational Linguistics: ACL-IJCNLP 2021
论文地址:https://arxiv.org/pdf/2105.14517.pdf
自动数学解题最近获得了越来越多的关注。自动数学解题大多数工作关注数学应用题自动求解。然而很少工作关注几何题。相比较于数学应用题,几何题需要同时对文本描述、图形图表进行理解,因为在几何题目中,题目文本和图形图表通常是相辅相成,缺一不可的。现有的几何题自动求解方法高度依赖规则并只在小数据集上进行评估。

图 4 几何题样例
为了推动几何题自动求解的研究,中山大学人机物智能融合实验室团队构建了一个由 5010 道几何选择题组成的问答数据集 GeoQA。如图 4 所示,GeoQA 数据集中的每一个样本具有题目描述、几何图像、问题选项、答案、问题类型、知识点、解答解析,以及按解题步骤标注的形式程序。在题目规模上,该数据集是前人工作常用的 GeoS 数据集的 25 倍。GeoQA 数据集的相关统计信息如下表所示。
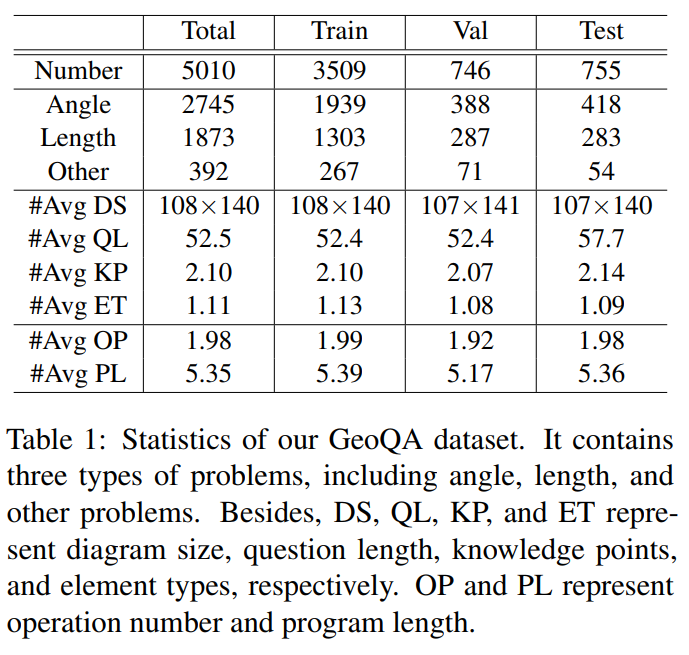
而 GeoQA 数据集所使用的形式程序算子和所涉及的常量如下表所示。

为了更好地促进几何题求解器的研究,我们除了在 GeoQA 数据集的基础上搭建了一些基线模型外,还提出了神经几何题求解器 NGS 来理解多模态语义信息并生成具有解释性的形式化程序。神经几何题求解器 NGS 的总体设计如图 5 所示。
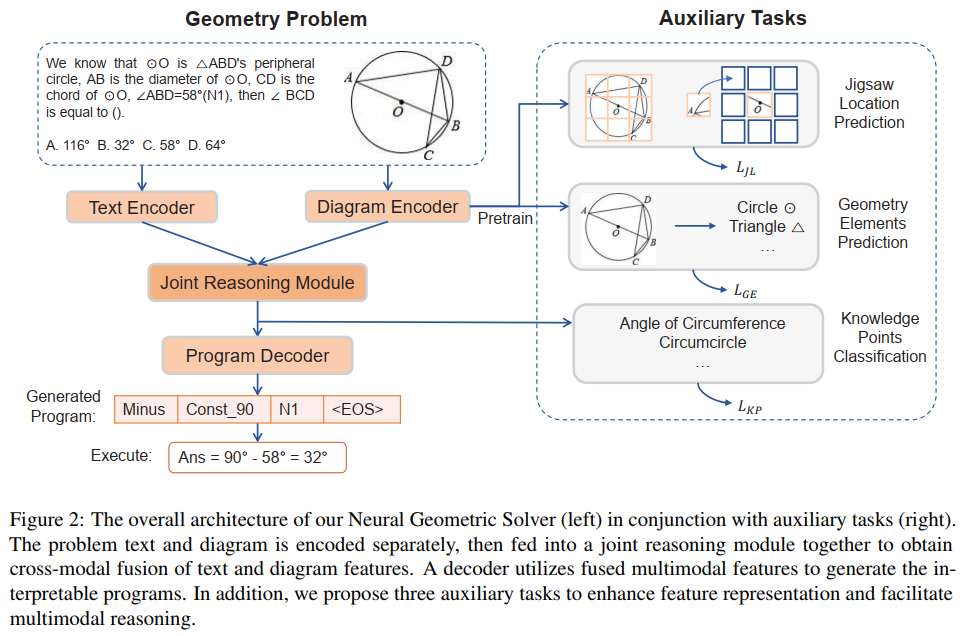
图 5 神经几何题求解器(NGS)示意图
我们的 NGS 主要由文本编码器、几何图形编码器,联合推理模块和程序解码器组成。文本编码器负责对题目文本语义表征,几何图形编码器则负责几何图形的表征。文本表征和图形表征均会输入到联合推理模型进行多模态语义表征,并投喂到程序解码器中进行程序解码,输出可解释可执行的形式化求解程序。
此外,为了增强几何图形编码器对几何图形的表征能力以及推进联合推理模块对题目所包含的多模态信息进行充分融合和高效表达,我们还引入了多种辅助任务来改善模型的表征能力和注入定理知识。这些辅助任务包括:1)拼图位置预测:通过把几何图形切割为多个 patch,并随机排列,然后让几何图形编码器对其重新排列,实现对几何图形的像素级图形理解;2)几何元素预测:让几何图形编码器学习预测哪些几何元素出现在了当前的几何图形中,实现对象级图形理解;3)知识点预测:在联合推理模块进行题目文本表征和几何图形表征的多模态融合的同时引入知识点分类任务来改进整体的问题表征。在 NGS 中,我们利用拼图位置预测和几何元素预测对几何图形编码器进行预训练。而知识点预测任务则作为一个子任务和 NGS 进行多任务训练。
在实验中,文章基于 GeoQA 构建了多个基于神经网络的基线模型,并将 NGS 与他们进行对比。NGS 和基线模型在 GeoQA 上的实验效果如下表所示。
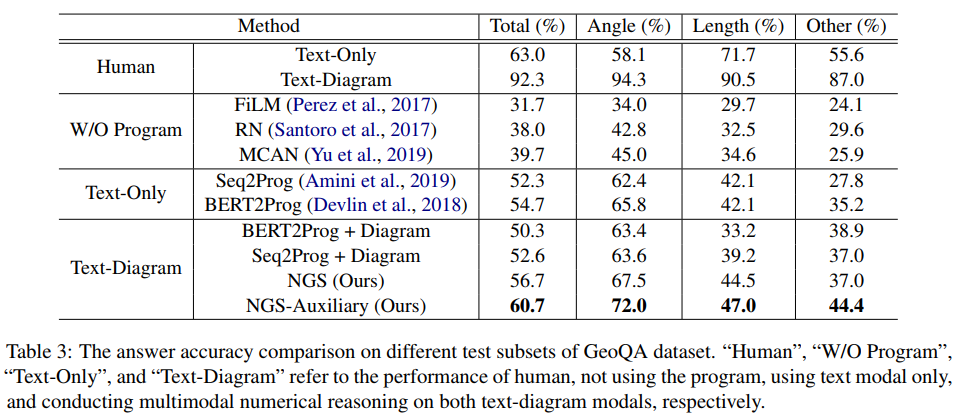
从上表可以看到,NGS 相比基线模型在 GeoQA 上能达到更好的解题性能。但是我们也可以看到各类模型与人类在几何题求解上仍然存在较大的差距。
此外,我们还进行了各种消融实验,验证了 NGS 中各种设计的有效性。更多研究细节,可参考原论文。
论文4:Unbiased Math Word Problems Benchmark for Mitigating Solving Bias

Findings of the Association for Computational Linguistics: NAACL 2022
论文地址:https://aclanthology.org/2022.findings-naacl.104.pdf
在这个工作中,中山大学人机物智能融合实验室团队重新审视在当前的数学应用题求解基准上评估模型的解题偏置(solving bias)。这种解题偏置主要数据偏置(data bias)和学习偏置(learning bias)引起。数据偏置(data bias)是指训练数据集未能涵盖每个问题的所有不同叙述方式而导致的解题模型只能学习到浅层语义,未能对题意进行深度语义理解的问题,如图 6(a)所示,由于解题模型只学习到浅层语义,并以此来进行解题, 那么即使我们把题目中的问题部分移除后,解题器仍然能达到 69.4%。
而学习偏置则是指一个 MWP 可以由多个等价的表达式来求解,但是当前的数据集均只采用其中某一个等价方程作为标签,强制模型学习该标签,而忽略了其他等价方程,导致学习训练的偏置。如图 6(b)所示,在训练过程中,模型可能会生成与 GroundTruth 表达式不一致但是答案是正确的表达式,但是由于数据集只采用了某一等价表达式作为标签,会导致在计算损失函数时认为该表达式是错误表达式,并将两个正确表达式之间的损失反向传播给求解模型,导致了模型的过度矫正。

图 6 数据偏置和学习偏置的示例
为了缓解数据偏置(data bias),中山大学人机物智能融合实验室团队作了一个新的尝试,我们以尽可能覆盖题目问法的方式重新标注了一个新的 MWP 基准 UnbiasedMWP。我们采集了 2907 到应用题作为基础问题,然后我们为每个问题中所蕴涵的故事标注尽可能多的问题。
为了简化人工标注过程,我们首先根据题目骨干的内容生成一些合理的表达式,然后再反向重写问题。为了生成合理的表达式,我们设计了三种表达式变种方式:1)Variable assortment (Va) 变形:从题目骨干随机选择两个数字变量,并使用数学运算符(+、-、*、/)对他们进行组合,例如 n0 + n1, n0 − n1 等。2)Subexpression (Sub) 变形:对原题目的目标表达式所蕴含的所有子表达是运算符的修改,从而获得新的表达式。3)Whole-expression (Whole)变形:通过改变原题目的目标表达式所包含的运算符来获取新的表达式。对于从上述三个变种获取得到的新表达式集进行人工过滤,过滤出无法进行新问题标注的表达式,对剩余表达式进行人工问题标注。
为了缓解学习偏置(learning bias),我们提出动态目标选择策略,在训练过程中根据模型输出的结果来选择与其更加接近的目标表达式来作为 GroundTruth。为了获得等价的表达式,我们利用数学运算中的交换律来对表达式树进行变形,从而获得多个等价的表达式。如图 7 所示。
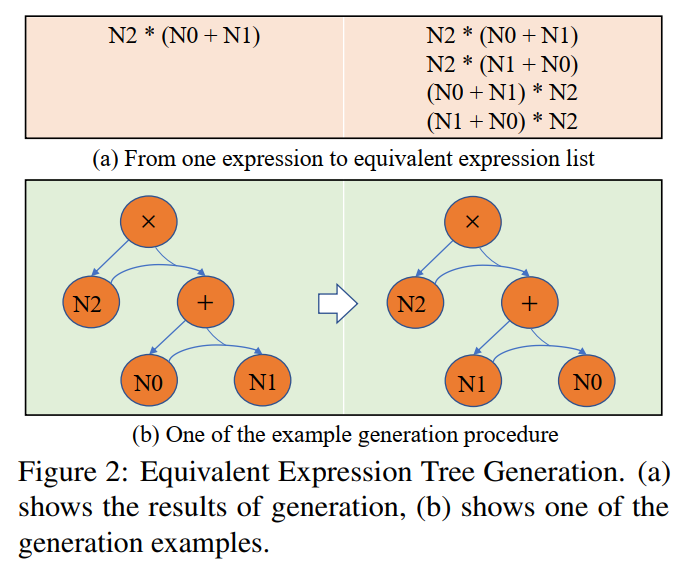
图 7 等价表达式树生成示意图
在实验中,文章首先在多个 SOTA 基线模型上对 UnbiasedMWP 数据集进行验证。其实验结果如下表所示。
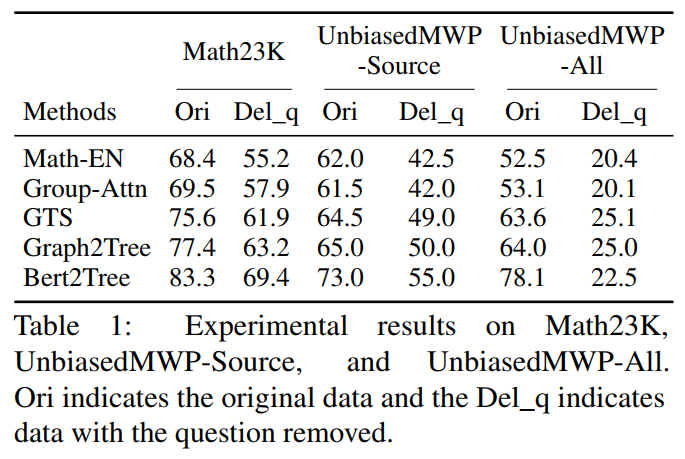
从实验结果可以看到,相比于现存的 Math23K,我们的数据集 UnbiasedMWP 所存在的数据偏置更少,因为当我们移除了题目问题后,模型的求解性能急剧下降,从侧面证明了我们的数据集更加能使得模型需要关注深层语义信息才能进行求解。
为了验证我们的动态目标选择策略是否能降低学习偏置,我们将动态目标选择策略应用在多个解题模型上。实验结果如下表所示。
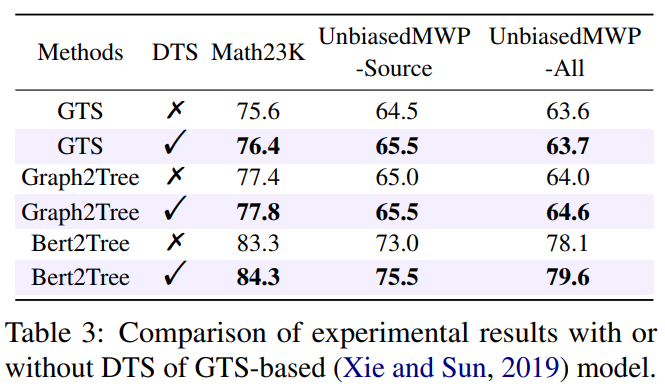
从实验结果可以看到,我们的动态目标选择策略能有效地降低学习偏置,并提升了模型的求解效果。更多研究细节,可参考原论文。
论文5:LogicSolver: Towards Interpretable Math Word Problem Solving with Logical Prompt-enhanced Learning

Findings of the Association for Computational Linguistics: EMNLP 2022
论文地址:https://arxiv.org/pdf/2205.08232.pdf
近年来,深度学习模型在数学应用题自动求解任务上取得了很大的成功,特别是在答案准确率方面。但是由于这些模型只利用了统计线索(shallow heuristics)实现了高求解性能,并没有真正地理解和推理题目背后的数学逻辑,因此,这些方法是难以解释的。
为了解决该问题并推动可解释数学应用题求解领域的发展,中山大学人机物智能融合实验室团队构建了第一个高质量的带解释的数学应用题数据集 InterMWP。该数据集包含了 11,495 道数学应用题和 210 种基于代数知识的逻辑公式,每道应用题的求解表达式均使用逻辑公式进行标注。与现有的数学应用题求解数据集不同,我们的 InterMWP 不仅要求解题器输出求解表达式,还要求解题器输出该求解表达式所对应的基于代数知识的逻辑表达式,从而实现对模型输出的解释。InterMWP 数据集与其他解题数据集的异同可以参考图 8。具体的标注过程可以参考原文。
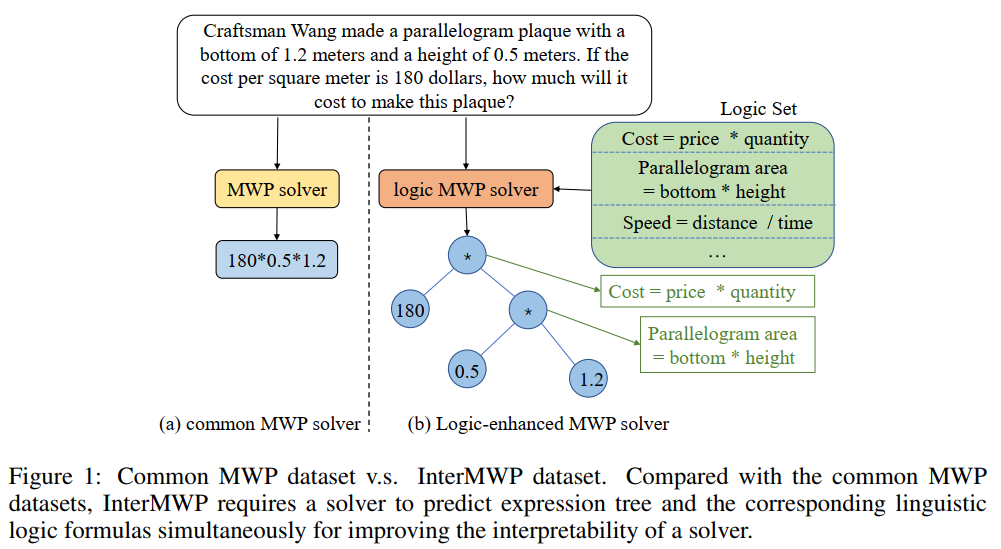
图 8 InterMWP 数据集示例
为了利用数学逻辑知识并赋能 MWP 解题器具备可解释性,我们团队进一步地构建了新的数学应用题求解框架 LogicSolver,如图 9 所示。该框架通过检索的方式从逻辑公式库提取相关的逻辑知识作为提示信息,改进问题编码器对 MWP 的语义表示的同时增强 MWP 的逻辑解释的生成能力。
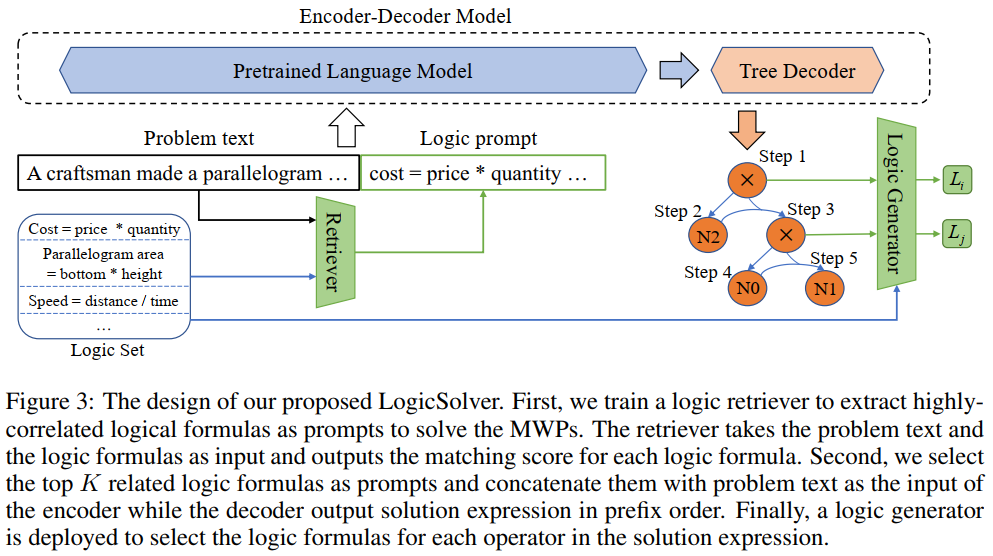
图 9 LogicSolver 设计示意图
LogicSolver 主要由逻辑知识检索组件、逻辑提示增强 MWP 求解器和解释生成组件三大组件构成。逻辑知识检索组件。对于每一道 MWP,我们从 210 种逻辑公式检索 top-k 个高度相关的逻辑公式作为提示,以增强 MWP 的求解。我们将逻辑公式提示与问题文本连接起来作为输入,驱动 MWP 模型生成求解表达式。最后,为了获取基于逻辑公式的解释,我们部署一个逻辑生成器来预测逻辑表达式树的每个内部节点(即运算符)所对应的逻辑公式作为求解的解释。
在实验中,我们在 InterMWP 数据集上构建了多个基线模型,并将我们的 LogicSolver 与这些基线模型进行对比。其实验结果如下表所示。
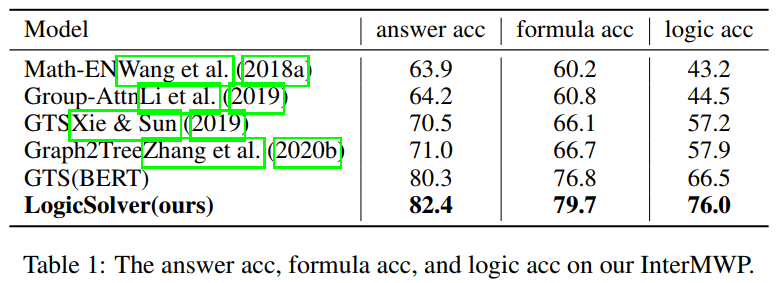
从实验结果可以看出,我们的 LogicSolver 在答案准确度,公式准确率,以及逻辑公式准确度上均能获得提升,说明了我们的 LogicSolver 在改善求解性能(Answer Acc 和 Formula Acc)的同时能具有更好的逻辑解释性(Logic Acc)。更多研究细节,可参考原论文。
论文 6:UniGeo: Unifying Geometry Logical Reasoning via Reformulating Mathematical Expression
Jiaqi Chen, Tong Li, Jinghui Qin, Pan Lu, Liang Lin, Chongyu Chen and Xiaodan Liang
The 2022 Conference on Empirical Methods in Natural Language Processing
几何题自动求解是一个用于评估深度模型多模态推理能力的基准。然而,在大多数现有的工作中,几何计算题自动求解和几何题自动证明通过会被视作两个不同的任务,并施加不同的标注处理,妨碍了深度模型在不同数学任务进行统一推理的研究进展。从本质上来说,几何计算题和几何证明题目具有相似的问题表达和解题所需的数学知识也有所重叠。因此,通过对几何计算题自动求解和几何题自动两个任务进行统一表示和学习有助于提升深度模型对这两种问题的语义理解和符号推理。
为此,中山大学人机物智能融合实验室团队构建了一个包含了数千道几何题的基准数据集 UniGeo。UniGeo 包括了 4,998 道几何计算题和 9,543 个几何证明题。我们对每个证明题均进行了多步骤证明标注,且这些标注可以很轻易地被转换为可执行的符号程序。而计算题也采用类似的标注,如图 10 所示。经过采用如图 10 所示的方式进行标注后,UniGeo 能很好地以形式化符号语言将几何计算题和几何证明题进行统一的表示。
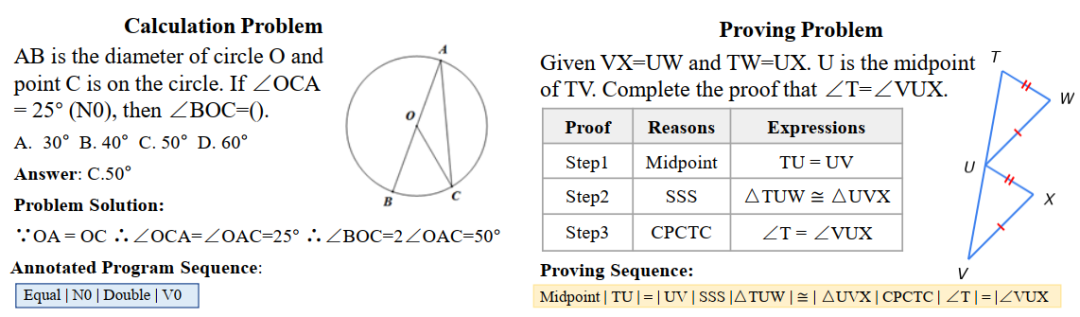
图 10 UniGeo 数据样例
在利用形式化符号语言对几何计算题和几何证明题进行统一标注后,为了验证这两种题目的统一表示能有效地促进模型对几何计算题和几何证明题的语义理解和符号推理能力,从而实现更高效的计算题求解和证明题证明。中山大学人机物智能融合实验室团队构建了面向几何题求解和证明统一处理的 Geoformer 来同时处理几何计算题和几何证明题,如图 11 所示。
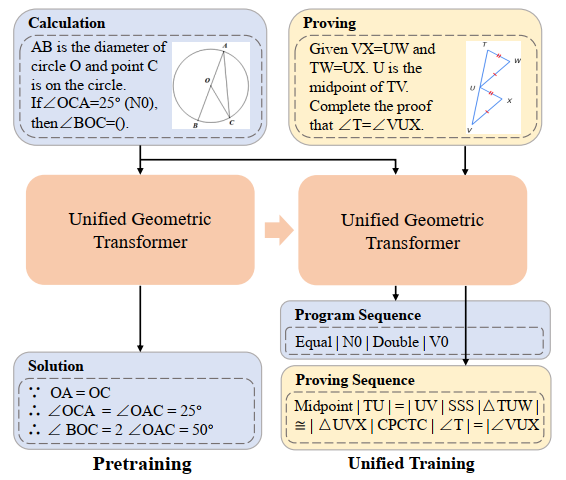
图 11 GeoFormer 示意图
此外,为了习得高效的 Geoformer 实现统一的几何推理,中山大学人机物智能融合实验室团队还进一步地提出数学表达预训练任务,结合 MLM 任务对 Geoformer 进行任务预训练,如图 12 所示。
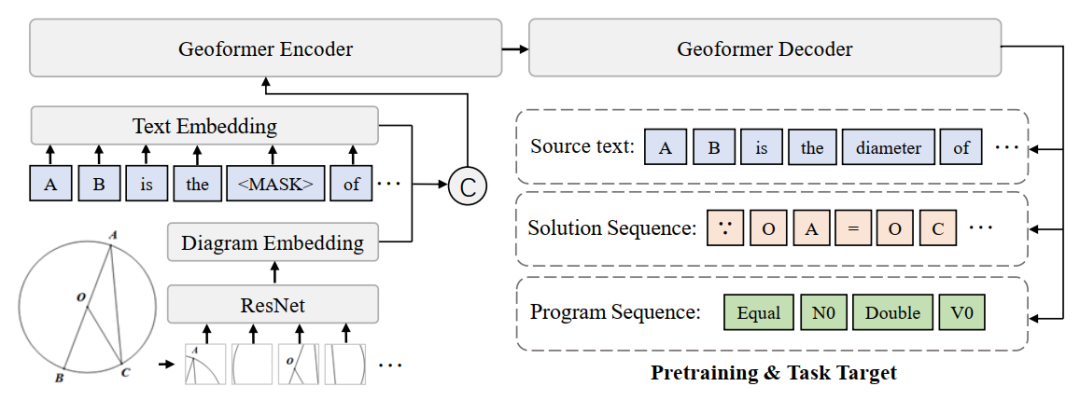
图 12 数学表达预训练示意图
在实验中,我们在 UniGeo 基准的基础上构建多个基线模型,并对我们提出的 GeoFormer 进行性能对比。实验结果如下表所示。
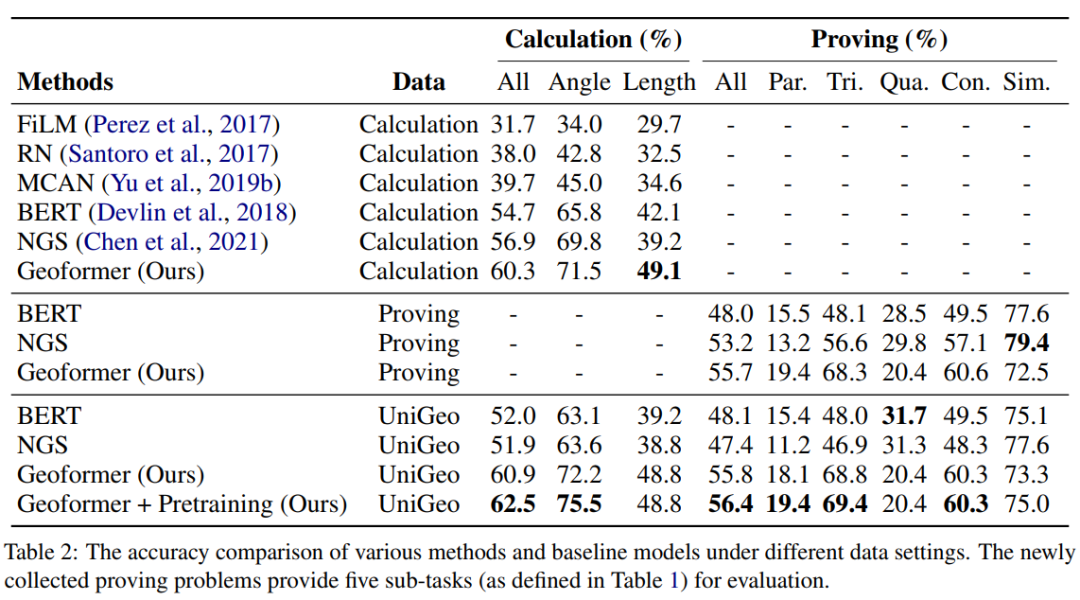
从实验结果可以看到,我们提出的 GeoFormer 在计算题和证明题两个子数据集上均能获得比基线模型更好的总体性能。类似地,在需要统一求解计算题和证明题的全数据集上 GeoFormer 相比 NGS 和 BERT 基线模型也是更优胜的。而在经过数学表达预训练和 MLM 预训练后,GeoFormer+Pretraining 相比 GeoFormer 会有进一步的性能提升。这些实验结果充分证明了 GeoFormer 的有效性,也说明了对几何计算题和几何证明题进行统一模型推理对于各自的任务来说也是有帮助的。
该工作已被 EMNLP2022 主会收录,更多研究细节,更多细节敬请期待。
论文 7:Template-based Contrastive Distillation Pre-training for Math Word Problem Solving
Jinghui Qin*, Zhicheng Yang*, Jiaqi Chen, Xiaodan Liang and Liang Lin
虽然深度学习模型在数学解题领域取得很好的进展,但是这些模型忽视了蕴涵在问题描述中的求解逻辑,而这种解题逻辑往往可以和解题模板(解法)相对应。如图 13 所示,两个不同的应用题均可以对应相同的解法。
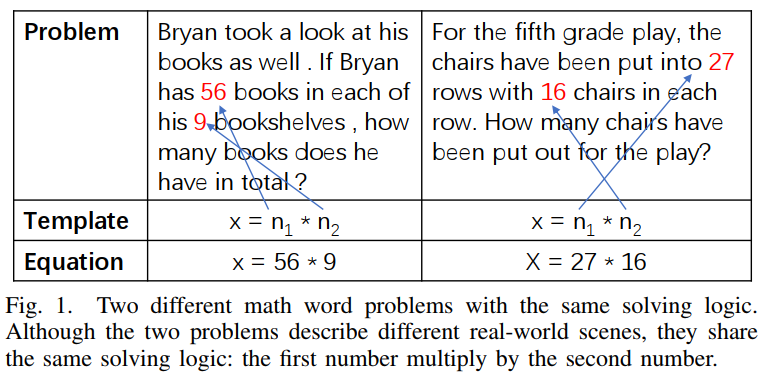
图 13 语言描述不同但解法相同的应用题示例
此外,预训练语言模型 (PLM) 包含丰富的知识和拥有高质量语义表示的能力,这对于 MWP 问题的求解会有帮助。
为了充分利用预训练语言模型所包含的丰富知识以及利用求解逻辑来更高效地求解应用题,中山大学人机物智能融合实验室团队提出基于解法模板和预训练语言模型的对比蒸馏预训练方法对求解器中的问题编码器进行领域预训练,如图 14 所示。该方法使用多视角对比学习有效地考虑数学逻辑知识的同时利用知识蒸馏的方式有效地保留了预训练语言模型中的知识和高质量语义表示能力。
具体来说, 我们首先以两道题目之间的解法模板是否一致来作为判定两道题目是否应该在表示空间上互相靠近的标识。然后,我们提出多视角对比学习,从教师编码器以及学生编码器及其对应的 Momentum 编码器进行对比学习,使得两道具有相同解法模板的题目表示在教师表示空间中和学生表示空间中进行互相靠近,从而实现解法逻辑的注入。此外,为了尽可能地保留以预训练语言模型进行初始化的学生编码器中所蕴涵的知识和高质量表示能力,我们使用知识蒸馏,利用教师编码器的特征表示作为监督,约束学生编码器的表示要与已训练好的教师编码器具有相同的表示能力,从而实现语义保持。
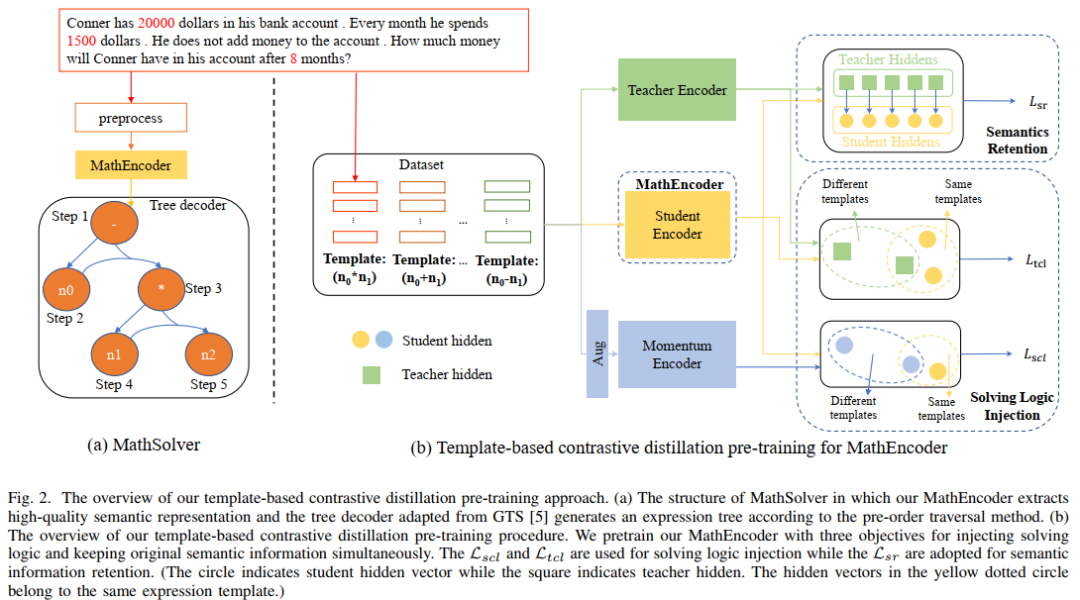
图 14 基于解法模板和预训练语言模型的对比蒸馏预训练方法
在实验中,我们使用不同的预训练语言模型作为初始化并验证我们方法的效果。我们分别使用 BERT-base 和 Roberta-base 权重对问题编码器 MathEncoder 进行初始化,并使用 GTS 中的 decoder 作为表达式解码器。我们统称基于 MathEncoder 的求解器为 MathSolver。我们将 MathSolver 与多个方法在 Math23K 和 CM17K 上进行了对比。实验结果如下表所示。
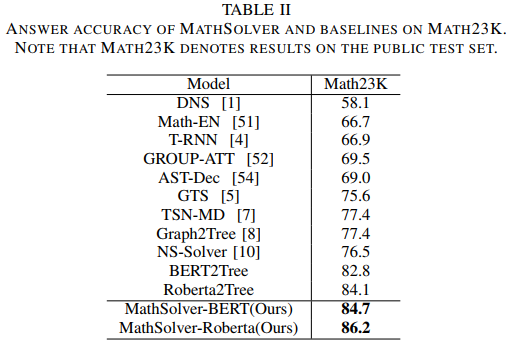
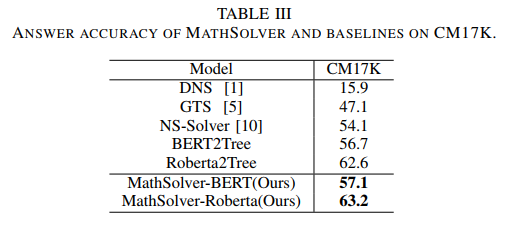
从实验结果可以看到,我们所提出的方法能有效地提升求解器的解题能力,并能在多种不同的预训练语言模型上进行应用。该成果已投稿到 IEEE Transactions on Neural Networks and Learning Systems,更多细节敬请期待。
论文 8:An Introspective Data Augmentation Method for Training Math Word Problem Solvers
Jinghui Qin, Zhongzhan Huang, Ying Zeng, and Liang Lin
近年来,越来越多的研究者开始研究基于深度学习的方法进行数学应用题自动求解,因为数学应用题自动求解能充分展示机器智能的程度。因为标注高质量大规模的 MWP 数据集的代价很高,比如需要相应教育程度的专业知识和大规模可访问的题目数据,所以现有的高质量 MWP 数据集的规模对于训练一个高效的 MWP 解题器是远远不够的。
MWP 的数据瓶颈问题鼓舞我们思考如何使用成本高效的数据增强方法来改进数据利用效率,提升求解器的性能。最直接的数据增强方法就是基于输入的数据增强方法,如常用的字符替换,字符删除等,但是这类方法对于 MWP 来说是不适用的,因为 MWP 具有言简意赅的特点,对输入的文本的扰动或修改容易使得题意模糊。此外,题意所蕴含的数学关系是不能被改变的,但这类方法很可能会改变题意所蕴含的数学关系,如图 15 所示。
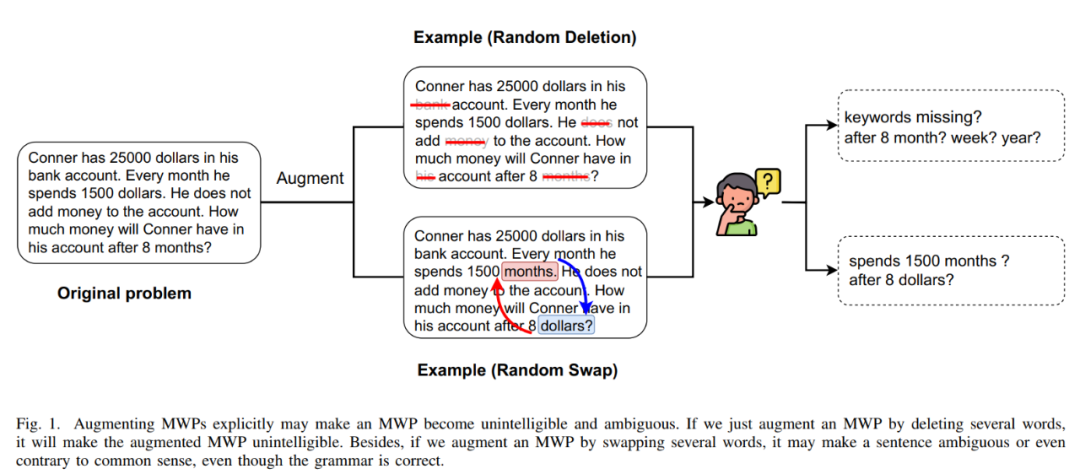
图 15 基于输入的数据增强方法不适用于 MWP 任务的示例
此外,中山大学人机物智能融合实验室团队还对基于输入的数据增强方法进行了一定的验证,其实验结果如图 16 所示。实验结果表明了基于输入的显式数据增强方法对于 MWP 任务来说是不适用的,无法有效地缓解 MWP 任务所遇到的数据瓶颈问题。
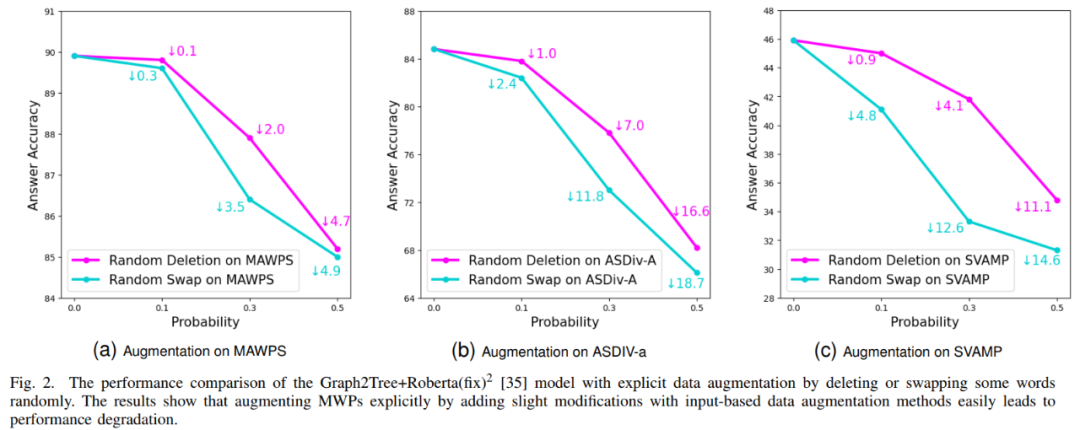
图 16 基于输入的数据增强方法无法提升 MWP 解题效果
为此,我们提出了一种适用于 MWP 数据的简单高效的数据增强方法 - 自省式数据增强方法(IDAM),在训练过程种对题目在隐空间的表示进行增强,从而解决了基于输入的数据增强方法在 MWP 求解任务上所遇到的问题。IDAM 方法通过对问题的表示编码执行不同的表示构建方法(均值池化、层次化聚合,随机丢弃,随机交换等),得到一个新的问题表示,然后使用一致性目标函数(基于表达式之间的 JS 散度)来约束求解器基于新问题表示的表达式解码输出要和基于原问题表示的表达式解码输出具有一致性。该方法的示意图如图 17 所示。
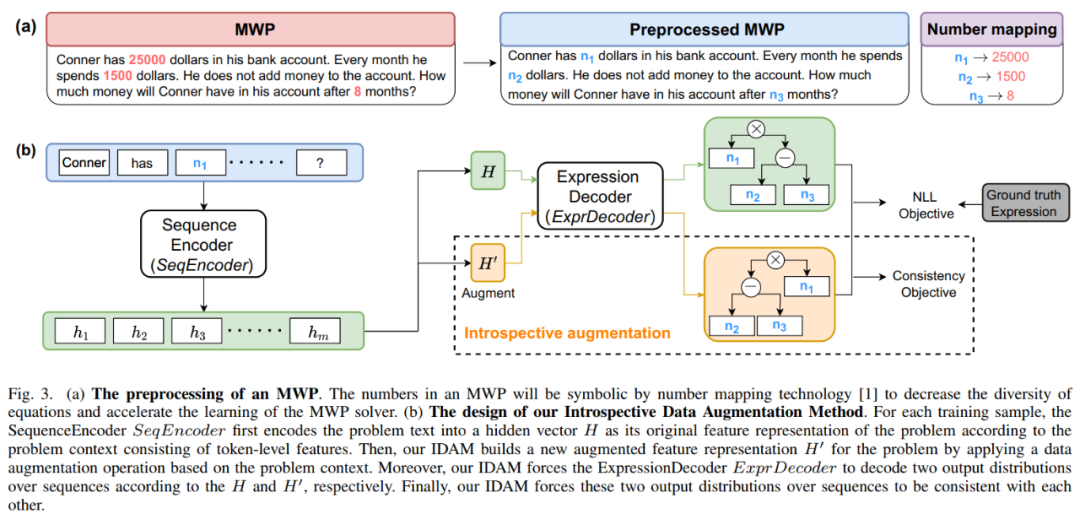
图 17 自省式数据增强方法(IDAM)示意图
在实验中,我们将 IDAM 嵌入到多个 SOTA 方法里并在多个数据集上进行了对比,验证了我们 IDAM 方法的有效性和通用性。实验结果如下表所示。从实验结果可以看到,在相同的实验配置下,我们的 IDAM 在不同的 MWP 数据集上均能对不同的求解器基线模型的性能进行提升。这充分说明了我们 IDAM 方法在 MWP 问题上的有效性。
该成果已投稿到 IEEE/ACM Transactions on Audio, Speech and Language Processing,更多细节敬请期待。
实验室简介
中山大学人机物智能融合实验室(HCP Lab)由林倞教授于2010年创办,围绕人工智能前沿技术布局研究课题,获得中国图像图形学会科技一等奖、吴文俊自然科学奖、省级自然科学一等奖等荣誉;培养了梁小丹、王可泽等国家级青年人才。