时间序列分解：将时间序列分解成基本的构建块-时间序列分解

大多数时间序列可以分解为不同的组件，在本文中，我将讨论这些不同的组件是什么，如何获取它们以及如何使用 Python 进行时间序列分解。

时间序列组成

时间序列是（主要）三个组成部分的组合：趋势、季节性和残差/剩余部分。让我们简单的解释这三个组成部分

趋势：这是该序列的整体运动。它可能会持续增加、也可能持续减少，或者是波动的。

季节性：系列中的任何常规季节性模式。比如，夏季冰淇淋的销量通常高于冬季。

残差：这是我们考虑到趋势和季节性后剩下的部分。它也可以被认为只是统计噪声，或者是临时性事件的影响，这个残差量也有一个单独的周期分量，但它通常被归入趋势分量。

加法模型与乘法模型

这些组件的组合方式取决于时间序列的性质。对于加法模型:

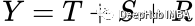
对于乘法模型:

其中 Y 是序列，T 是趋势，S 是季节性，R 是残差分量。

当序列变化的大小尺度一致的时候，加法模型是最合适的。而当序列的波动处于相对和比例范围内时乘法模型是比较合适的。

例如，如果夏季冰淇淋的销量每年高出 1,000 个，则该模型是加法的。如果每年夏天销售额持续增长 20%，但绝对销售额在变化，则该模型是乘法的。稍后我们将讨论一个示例，该示例可以使该理论更加具体。

为了计算和可视化的渐变，可以通过对数变换或Box-Cox变换将乘法模型转换为加法模型:

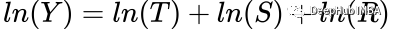
分解是如何工作的

有多种算法和方法可以将时间序列分解为三个分量。以下的经典方法，经常会使用并且非常直观。

使用移动/滚动平均值计算趋势分量 T。
对序列进行去趋势处理，Y-T 用于加法模型，Y/T 用于乘法模型。
通过取每个季节的去趋势序列的平均值来计算季节分量 S。
残差分量 R 的计算公式为：对于加法模型R = Y-T-R，对于乘法模型R = Y/(TR)。

还有其他几种可用于分解的方法，例如 STL、X11 和 SEATS。这些是先进的方法，是对经典方法的基本方法的补充，并改进了它的缺点。如果有想了解这些最新方法的可以留言，我们单开一篇文章介绍。

Python中进行时间序列分解

这里让我们使用1948年至1961年的美国航空客运量数据集:

#https://www.kaggle.com/datasets/ashfakyeafi/air-passenger-data-for-time-series-analysis
 
 import plotly.express as px
 import pandas as pd
 
 # Read in the data
 data = pd.read_csv('AirPassengers.csv', index_col=0)
 data.index = pd.to_datetime(data.index)
 
 # Plot the data
 fig = px.line(data, x=data.index, y='#Passengers',
  
 
 fig.update_layout(template="simple_white", fnotallow=dict(size=18),
  
 
 fig.show()

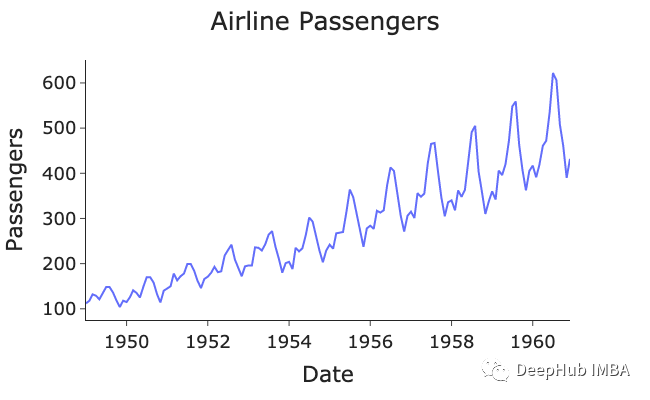
从图中我们观察到趋势是增加的，每年也有季节性。波动的大小随着时间的推移而增加，因此我们可以说这是一个乘法模型。

statmodels中包含了seasonal_decomposition函数可以帮我们来分解时间序列，并在我们要在调用函数时指定这是一个“乘法”模型:

from statsmodels.tsa.seasonal import seasonal_decompose
 import matplotlib.pyplot as plt
 
 # Plot the decomposition for multiplicative series
 data.rename(columns={'#Passengers': 'Multiplicative Decomposition'}, inplace=True)
 decomposition_plot_multi = seasonal_decompose(data['Multiplicative Decomposition'],
  
 decomposition_plot_multi.plot()
 plt.show()

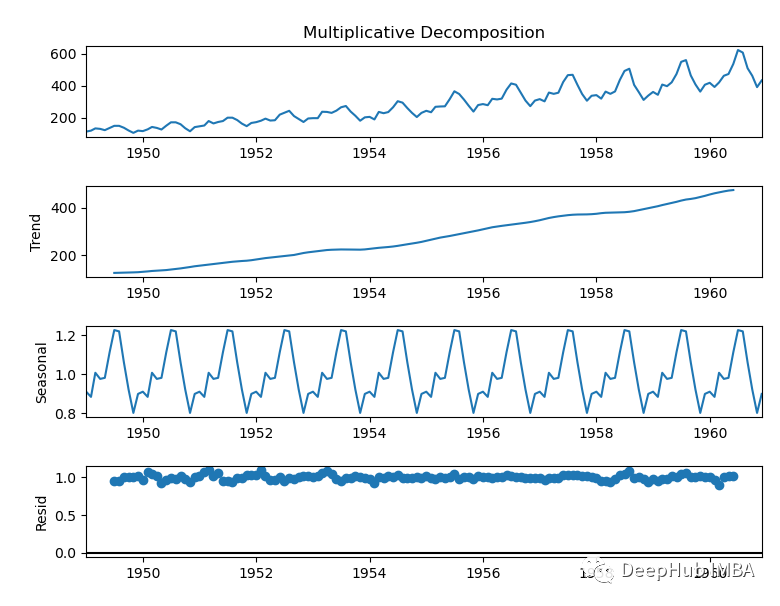
从上图中可以看到，该函数确实成功地捕获了这三个组成部分。

通过应用Scipy的函数boxcox ，可以使用Box-Cox变换稳定方差，这样可以将序列转换为一个加法模型:

# Import packages
 from statsmodels.tsa.seasonal import seasonal_decompose
 import matplotlib.pyplot as plt
 from scipy.stats import boxcox
 
 # Apply boxcox to acquire additive model
 data['Additive Decomposition'], lam = boxcox(data['#Passengers'])
 
 # Plot the decomposition for additive series
 decomposition_plot_add = seasonal_decompose(data['Additive Decomposition'],
  
 decomposition_plot_add.plot()
 plt.show()

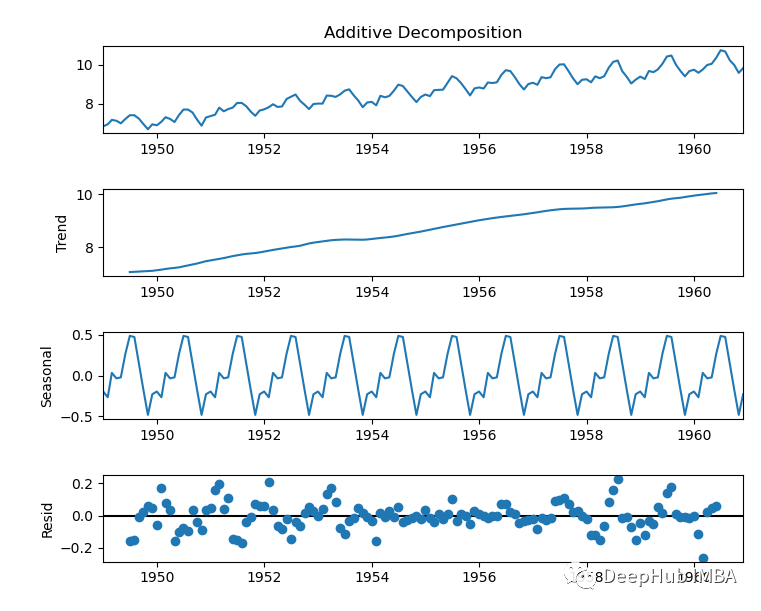
这个函数也很好地捕获了这三个组件。但是我们看到残差在早期和后期具有更高的波动性。所以在为这个时间序列构建预测模型时，需要考虑到这一点。

总结

在这篇文章中，我们展示了如何将时间序列分解为三个基本组成部分:趋势、季节性和残差。这三个组成部分的组合产生了实际的时间序列，它们的组合可以是加性的也可以是乘性的。有几种更新技术可以执行分解，如STL, SEAL和X11，但是经典的方法简单并且直观。最后通过分解时间序列有助于建立对数据的理解，从而更容易做出未来的预测。