本文经AI新媒体量子位(公众号ID:QbitAI)授权转载,转载请联系出处。
用AI求解偏微分方程,这段时间确实有点火。
但究竟什么样的AI求解效果最好,却始终没有一个统一的定论。
现在,终于有人为这个领域制作了一个名叫PDEBench的完整基准,论文登上了NeurIPS 2022。
PDEBench不仅能当成一个大型偏微分方程数据集,也能作为新AI求解偏微分方程的基准之一——
不少“老前辈”的预训练模型代码都能在这里找到,作为一个比对基础。
例如去年大火了一阵的FNO,几秒钟求解出传统方法需要计算18个小时的偏微分方程,代码就被放进了PDEBench中。
这个新基准一出,LeCun也激情转发:这领域确实很火。
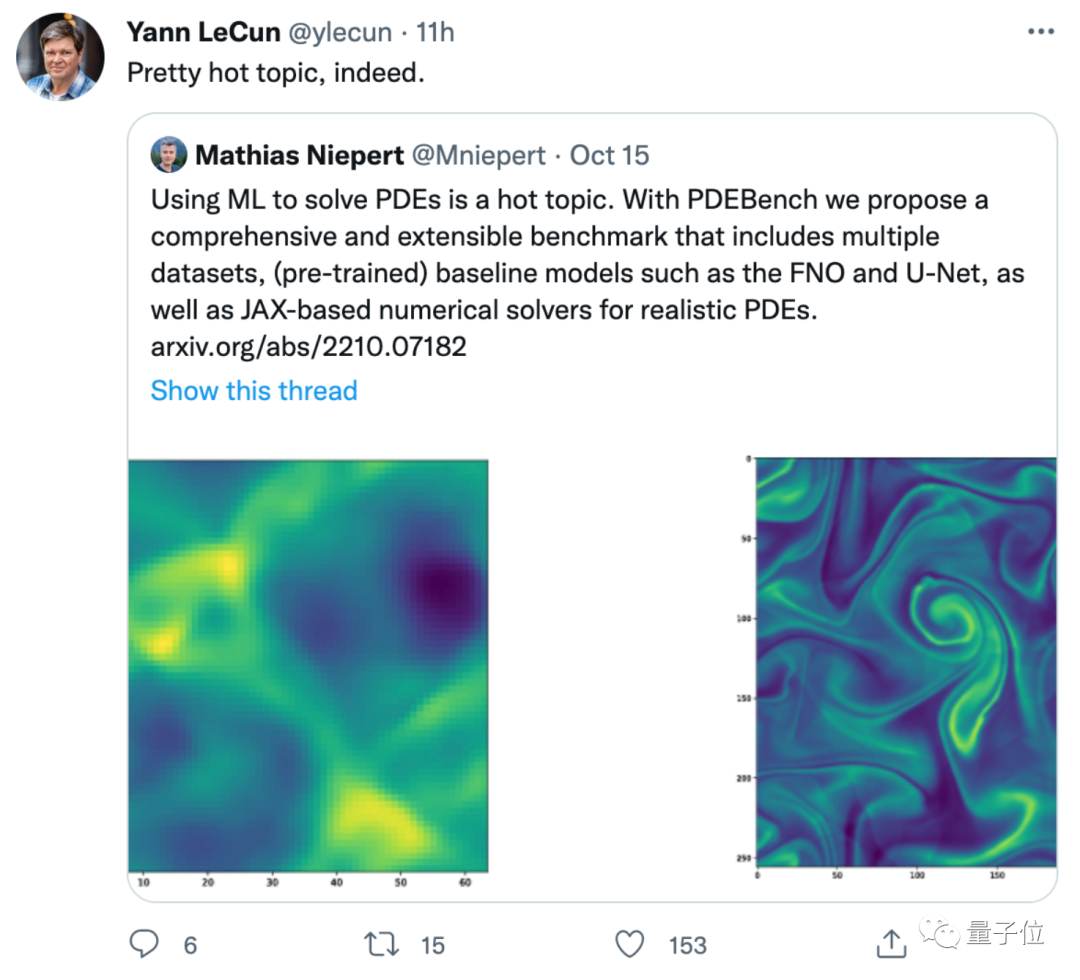
所以,AI求解偏微分方程的优势是什么,这一基准具体提出了哪些评估方法?
为啥用AI求解偏微分方程?
偏微分方程(PDE,Partial Differential Equation),是一个生活中常见的方程。
包括预报天气、模拟飞机空气动力、预测疾病传播模型,都会用到这个方程。
目前北大数学系“韦神”韦东奕的研究方向之一,就是流体力学中的数学问题,其中就包括偏微分方程中的Navier-Stokes方程。
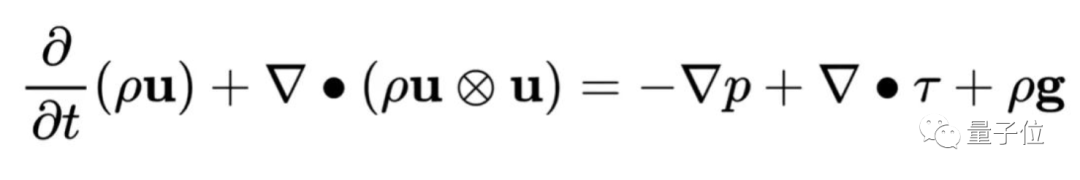
所以,为啥要用AI来求解偏微分方程?
训练AI的本质,是找到一种尽可能逼近真实结果的模型。
用AI求解偏微分方程,其实也是找到一种代理模型,来模拟偏微分方程模型。
代理模型,指找到一种近似模型,在计算量更小的同时,确保计算结果与原来的偏微分方程尽可能相似。
这与传统的数值方法求解偏微分方程有着异曲同工之妙。
传统方法往往需要通过将连续问题离散化(类似在一个连续函数上切割出很多小点),来对方程进行近似求解。
然而,传统的数值方法非常复杂,计算量也很大;采用AI方法训练出来的模型,却模拟得又快又好——
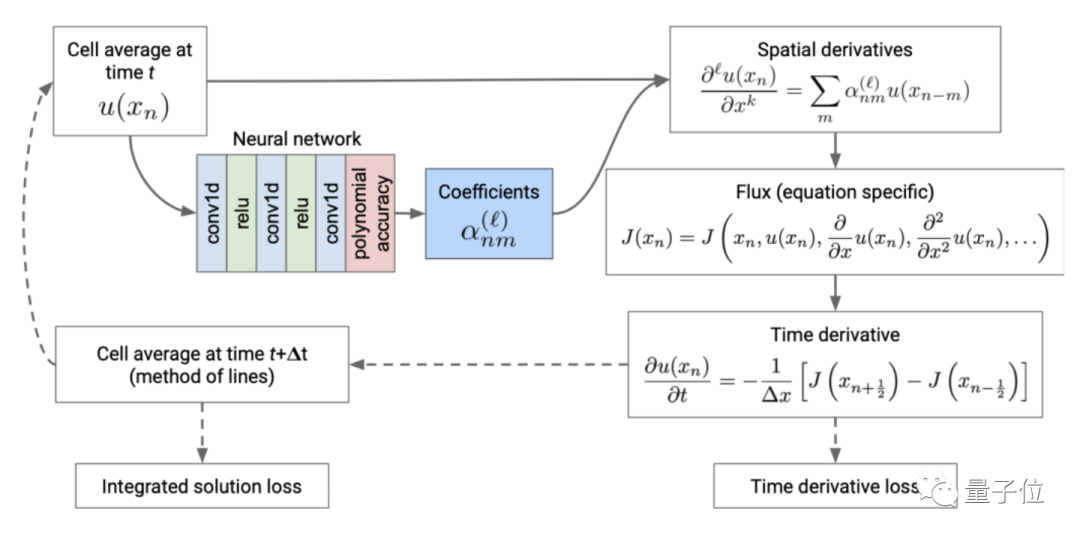
继2017年华盛顿大学提出PDE-FIND后,2018年谷歌AI又提出了数据驱动求解偏微分方程的方法,都比传统方法要快上不少,让更多人开始关注到AI求解偏微分方程这一领域。
2019年,布朗大学应用数学团队提出一种名叫PINN (物理激发的神经网络)的方法,彻底打开了AI在物理学领域的广泛应用。
这篇论文在理论上虽然没有PDE-FIND和谷歌AI的方法突破性强,却给出了非常完整的代码体系,使得开发人员很容易上手,让更多研究者开发出了不同的PINN,如今它也成为AI物理最常见的框架和词汇之一。
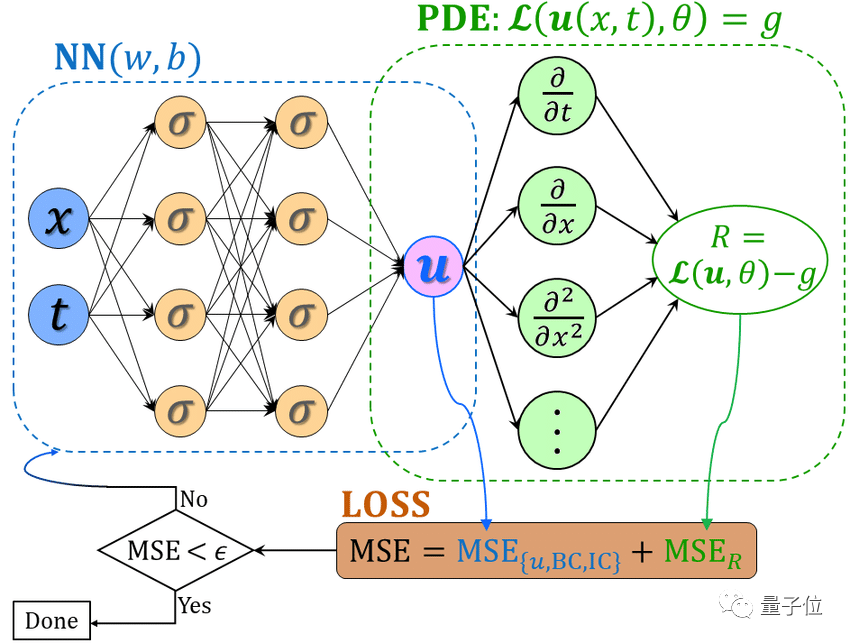
△PINN
去年加州理工大学和普渡大学团队发表的一项研究,更是将偏微分方程计算时间从传统求解的18个小时降低为1秒钟。
这篇论文提出了一种名为FNO (傅里叶神经算子)的方法,基于傅里叶变换给神经网络加上“傅里叶层”,进一步节省了近似模拟算子的计算量。
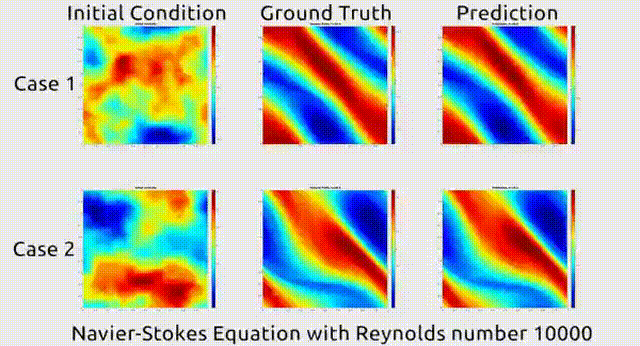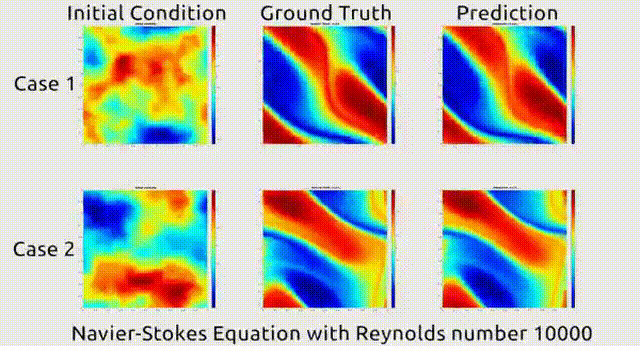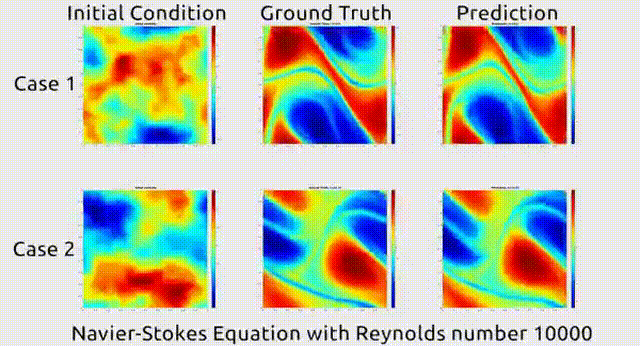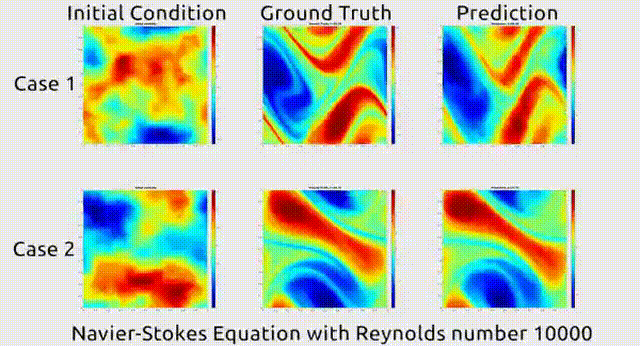
除此之外,也有不少研究人员通过训练一些经典AI模型,来求解偏微分方程,如U-Net等。
不过,无论是FNO、U-Net还是PINN,都还是基于各自给出的基准来评估AI计算偏微分方程的效果。
有没有一个更统一、更通用的框架来评估这个领域的新突破?
更全面的AI偏微分方程基准
在这样的背景下,研究人员提出了一种名叫PDEBench的基准。
首先是基准中包含的数据集,目前这些数据集已经全部归纳到GitHub中:
这里面包括不少经典偏微分方程问题,如Navier-Stokes方程,达西流模型、浅水波模型等等。
随后,PDEBench提出了几个指标,来从不同角度更全面地对AI模型进行评估:
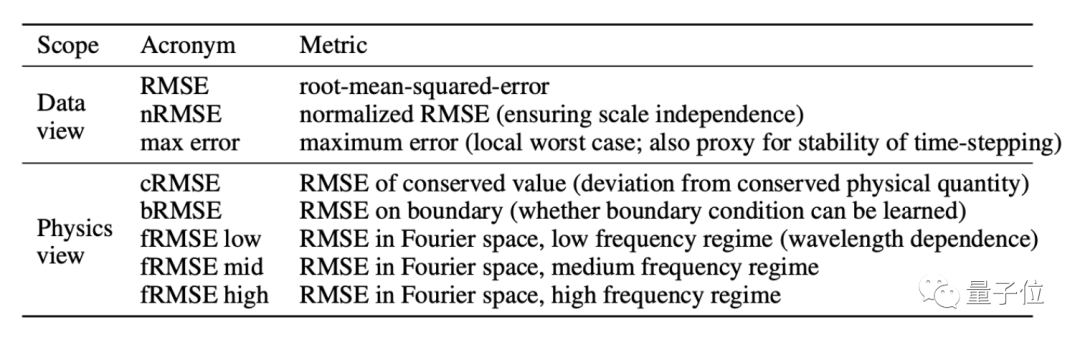
最后,PDEBench还包含了几种经典模型的预训练模型代码,并将它们作为评估其他模型的基准之一,包括上述提到的FNO、U-Net、PINN等。
例如研究团队将这几个模型分别基于各数据集进行了训练,得出的均方根误差(RMSE)如下,也说明它们在不同偏微分方程问题上的表现并不一样:
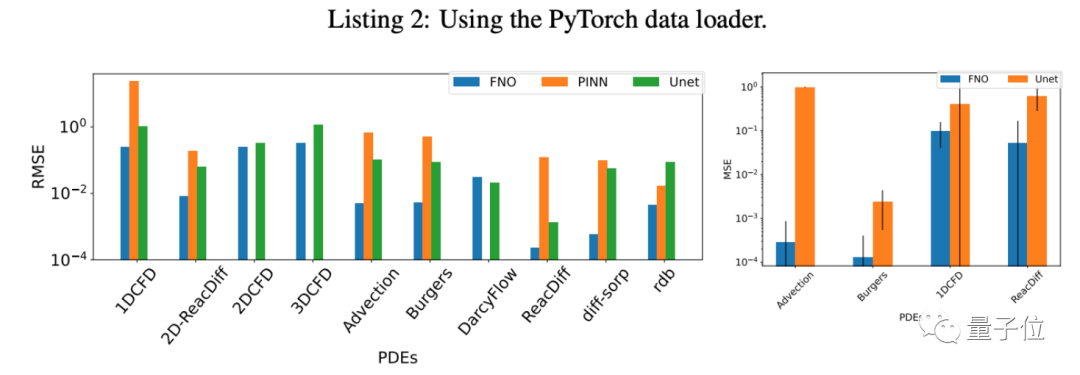
除此之外,团队还将数据格式进行了统一,同时针对PDEBench的可扩展性进行了优化,因此任何人都能参与进来,给这一基准加入更多的数据集、或是更多基准模型。
值得注意的是,团队试了试分别在PyTorch和JAX两种框架上运行几种预训练模型,发现JAX的速度大约是PyTorch的6倍。
看来以后搞相关研究可以试试JAX框架了。
作者介绍
作者们来自德国斯图加特大学,欧洲NEC研发中心,还有澳大利亚联邦科学与工业研究组织(CSIRO)旗下的Data61数字创新中心。
Makoto Takamoto,欧洲NEC研发中心高级研究员,毕业于京都大学,研究方向是图像处理、图神经网络和科学机器学习。
Timothy Praditia,斯图加特大学博士研究生,研究兴趣是开发基于数据驱动和先验物理知识的神经网络模型。
论文地址:https://arxiv.org/abs/2210.07182
PDEBench地址:https://github.com/pdebench/PDEBench