我们可以用来更好地理解趋势(或帮助模式识别/预测算法)的一种方法是时间序列平滑。以下传统的方法:
移动平均线——简单、容易、有效(但会给时间序列数据一个“滞后”的观测),Savitzky-Golay过滤器——有效但更复杂,它包含了有一些直观的超参数
还有一个不太传统的方法是解热方程,它有更直观的超参数,而且也非常快!在本文中,我们将考虑一个稍微复杂一些的方程,但它具有保存边缘的效果。
这个方程叫做Perona-Malik PDE (偏微分方程),它的平滑效果可以在下面的动图中看到:
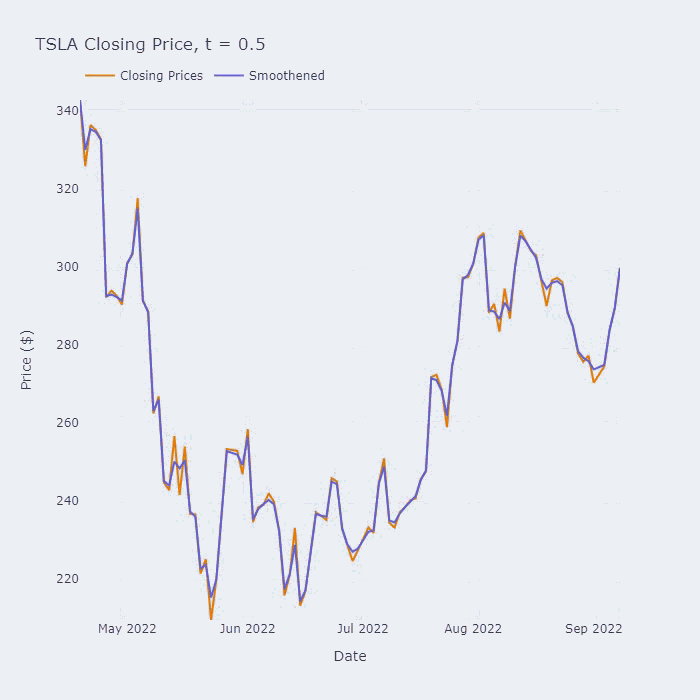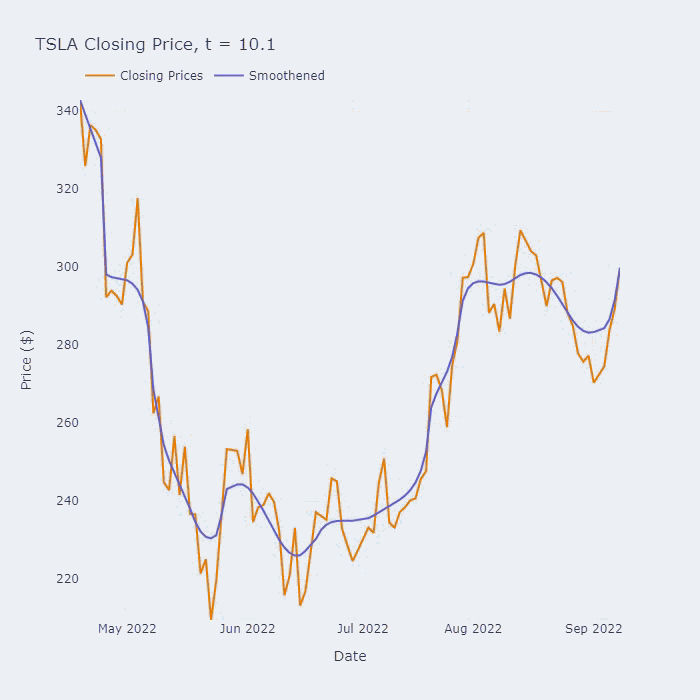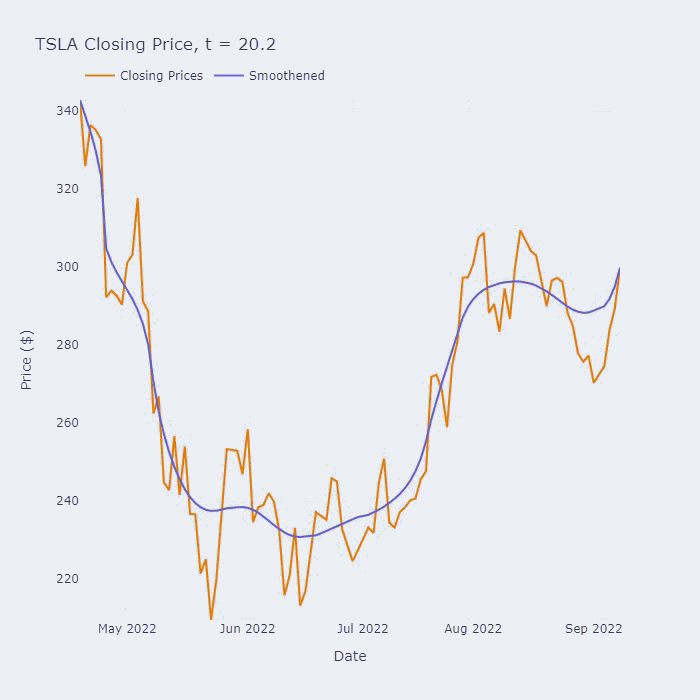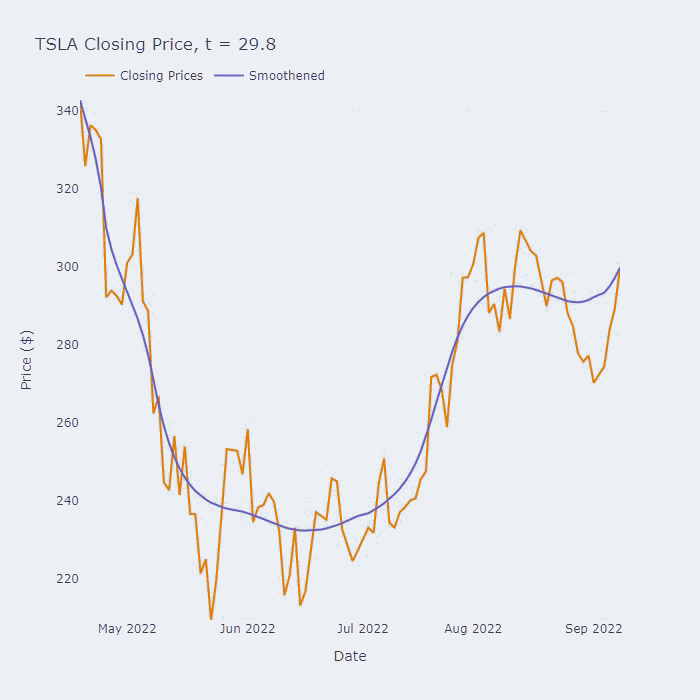
上图是该保持边缘平滑方法在用于于特斯拉(TSLA)在2022年的收盘价的效果。标题中的“t=x”对应于我们平滑级数的时间(以非维度单位)。
如果你对上面的效果感兴趣,那么本文将解释以下内容:
- Perona-Malik PDE(偏微分方程),以及为什么要使用它
- 如何求解偏微分方程。
- 和热方程的比较
Perona-Malik PDE
下面是将要处理的方程公式:
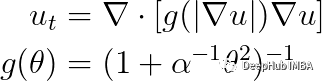
Perona-Malik PDE。式中u是我们要平滑的时间序列,α是控制边保的参数(α越小对应的边保越多)。
看着有点复杂,我们继续解释。当我们试图解决这个PDE的原始形式时,它会导致一些问题;所以我们要考虑一种修改后的形式:
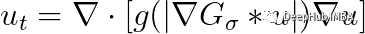
基本上,函数g的内部进行了一次高斯函数卷积(也就是说,它变得更平滑了)。这被称为正则化,我们只要知道它是可解的就可以了
这个一个可怕的等式比上面更复杂了,但是这我们没有多个空间维度,我们在平滑的是一个时间序列,所以它只有一个维度。所以需要解的方程是:
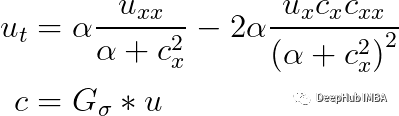
这样看着就简单多了,至少所有的字母我们都认识了😁,但是如果想了解细节,可以通过扩展和简化得到上面的公式进行推导,虽然不建议这么做,但是如果你喜欢的话那随意。
我们刚提到处理的时间序列是一维的,但是为什么偏微分方程是二维的?
这个偏微分方程是根据时间来求解的。从本质上讲时间上的每一步都使数据进一步平滑。所以t越大,时间序列越平滑,这意味着空间变量x表示时间序列中的“时间”,后面的求解会详细解释。
为什么要用这个方程呢?
热方程的问题是它不能很好地保存边。保留这些边缘来捕捉价格的大幅快速波动可能是可取的,但要去除任何小但高频的噪声。
这种方法比热方程更难,因为Perona-Malik PDE是非线性的(不像热方程是线性的)。一般来说,非线性方程不像线性方程那么容易求解。
如何求解这个偏微分方程
我们将使用一种称为有限差分(finite differences)的方法。它是一种求偏微分(或常微分)方程和方程组定解问题的数值解的方法。你可以将其视为每次我们在下图中遇到交集时找到解决方案:
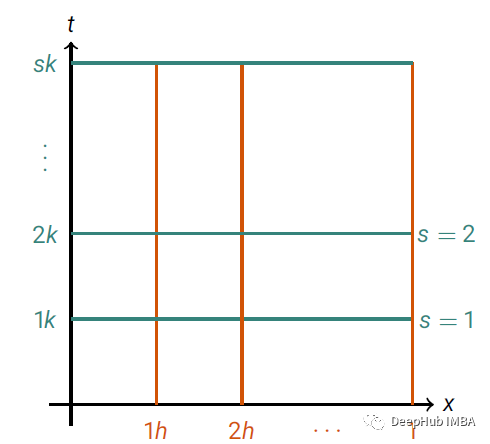
随着时间和空间分裂成离散间隔的图示。这里空间中的离散区间是从 [0, 1] 开始的,时间上的离散区间是从 t=0 到 t=sk,其中 s 是我们获取的区间。线的交点是我们找到偏微分方程解的位置。
在处理数字之前,我们需要用数学方法来定义整个问题。由于方程在空间上是二阶的,在时间上是一阶的,所以需要两个边界条件和一个初始条件:
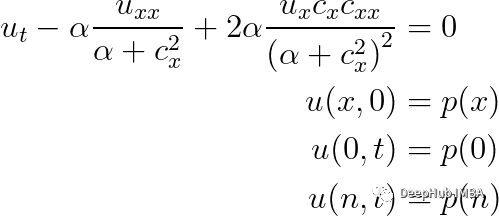
我们将求解以平滑时间序列的方程组(这个方程看起来比代码复杂得多!),我们的起点是股票价格时间序列,并且终点总是具有相同的价格。
那么我们如何从数值上开始求解呢?我们最初的方法是用这些导数的有限差分近似,Perona-Malik PDE中导数的近似值,这些导数的推导超出了本文的范围,所以就不详细写了。

上面公式中,h和k分别是空间和时间离散点之间的距离。这里可以使用相同的公式计算 c 的导数。
在我们的问题中,空间中的离散点被分开一天,所以 h = 1。建议使用 k < 0.1 的值来保持有限差分公式的一些准确性。因为如果k 值太大,则有限差分方案会变得不稳定。
我们现在需要将这些近似值放入偏微分方程中……这会让公式看起来更加复杂😢,这是我的计算代数软件给出的结果:
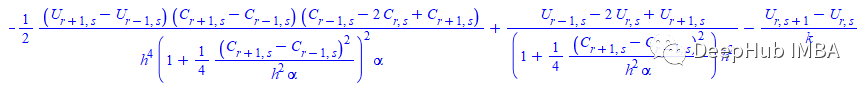
这就是Perona-Malik PDE的离散形式,越来越复杂了。有没有更好的方法呢?
我们可以偷懒并使用微分矩阵。因为时间序列是一组离散点,所以可以使用矩阵向量乘积进行微分。
如果以前从未听说过这个,那么这里有一些代码展示了如何使用矩阵向量积计算多项式的简单导数:
import numpy as np
import plotly.io as pio
import plotly.graph_objects as go
pio.renderers.default='browser'
if __name__ == '__main__':
n = 100 # The number of discrete points
a = -4 # The interval starting point
b = 4 # The interval ending point
# The discrete points and spacing
x = np.linspace(a, b, n)
h = (b-a)/n
# Function to differentiate, and its analytical derivative for checking
f = 10*x**3 + x**2
fx = 30*x**2 + 2*x
# Form the differentiation matrix
Dx = (
np.diag(np.ones(n-1), 1)
- np.diag(np.ones(n-1), -1)
)/(2*h)
# Calculate the numerical derivative on the interior only
Ux = Dx[1:-1, :]@f
# Plot the figure
fig = go.Figure()
fig.add_trace(go.Scatter(x = x, y = f, name = 'Function'))
fig.add_trace(go.Scatter(x = x, y = fx, name = 'Analyitcal Derivative'))
fig.add_trace(
go.Scatter(
x = x[1:-1],
y = Ux,
name='Finite Difference Derivative',
line={'dash': 'dash'}
)
)
fig.update_layout(
yaxis = {'title': 'f(x), f_x(x)'},
xaxis = {'title': 'x'},
title = 'Finite Difference Derivative Test',
legend = {'x': 0, 'y': 1.075, 'orientation': 'h'},
width = 700,
height = 700,
)
fig.show()
以上代码应该产生以下输出:
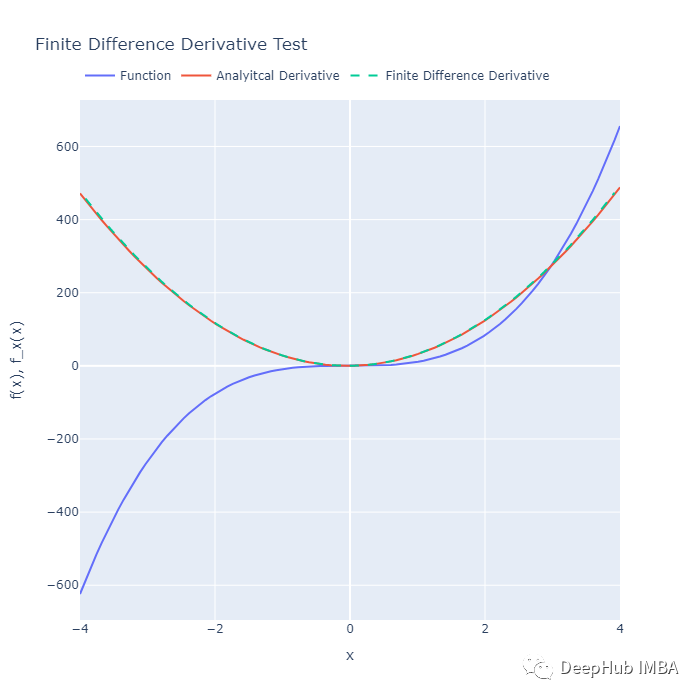
使用矩阵向量积可以对简单多项式求导。它本质上是一阶导数的有限差分逼近

已转化为矩阵向量乘积,使用下面的代码:
Dx = (
np.diag(np.ones(n-1), 1) # u_{r+1, s} terms
- np.diag(np.ones(n-1), -1) # u_{r-1, s} terms
)/(2*h)# Calculate the numerical derivative on the interior only
Ux = Dx[1:-1, :]@f
通过使用这种有限差分公式,我们只能找到内部点的导数。比如在域的第一个点 (x = r = 0) 有近似值:

虽然这是没有意义的,因为需要的计算点在域之外。但是这对我们来说不是一个问题——因为我们只解内部点的偏微分方程,而这些解在端点处是固定的。
我们使用一个简单的小系统的离散方程(比如有5个离散点),上面的解释可能会清晰得多。
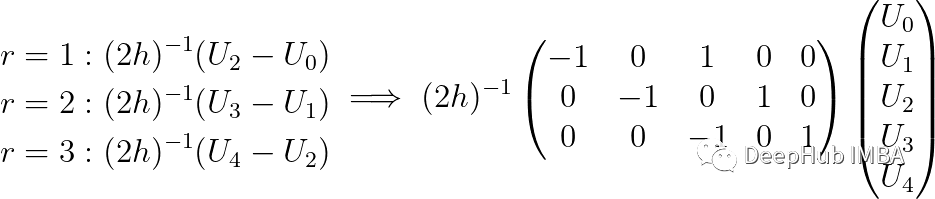
还有最后一个问题卷积是如何执行的?最简单的方法是使用scipy. nimage.gaussian_filter,但是这里我选择的方法是解热方程,通过一点数学技巧,可以证明高斯卷积可以解决热方程。换句话说,我们要解
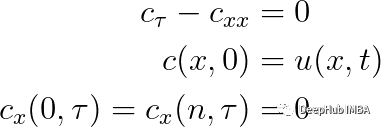
这可以用离散形式表示为:
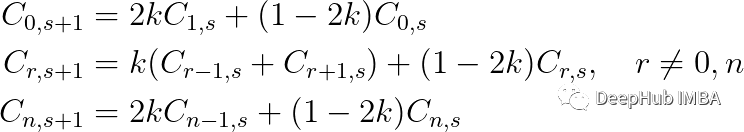
高斯滤波中的标准差(σ)与我们通过σ²(τ) = 2τ求解上述方程的“时间”量有关,所以,要解的时间越长,标准差越大,时间序列就越平滑。
为什么要用这种方式进行卷积?偏微分方程到卷积的连接非常简洁!并且因为可以将偏微分方程求解逻辑硬编码为循环,所以将其包装在@numba.jit装饰器中,提高了计算效率。
Python实现
现在我们已经在数学方面做了艰苦的工作,编码就变得非常直接了!
卷积的实现如下所示:
import numpy as np
def convolve_PDE(U: np.array,
sigma: float = 1,
k: float = 0.05) -> np.array:
'''
Perform Gaussian convolution by solving the heat equation with Neumann
boundary conditions
Parameters
----------
U : np.array
The array to perform convolution on.
sigma : float, optional
The standard deviation of the guassian convolution.
k : float, optional
The step-size for the finite difference scheme (keep < 0.1 for accuracy)
Returns
-------
U : np.array
The convolved function
'''
t = 0
t_end = sigma**2/2
while t < t_end:
# Implementing the nuemann boundary conditions
U[0] = 2*k*U[1] + (1-2*k)*U[0]
U[-1] = 2*k*U[-2] + (1-2*k)*U[-1]
# Scheme on the interior nodes
U[1:-1] = k*(U[2:] + U[:-2]) + (1-2*k)*U[1:-1]
t += k
return U
代码看起来就很简单了,对吧?Perona-Malik求解器的实现也不复杂:
def get_diff_mat(n: int) -> Tuple[np.array, np.array]:
'''
Get the first and second differentiation matrices, which are truncated
to find the derivative on the interior points.
Parameters
----------
n : int
The total number of discrete points
Returns
-------
[Dx, Dxx] : np.array
The first and second differentiation matrices, respecitvely.
'''
Dx = (
np.diag(np.ones(n-1), 1)
- np.diag(np.ones(n-1), -1)
)/2
Dxx = (
np.diag(np.ones(n-1), 1)
- 2*np.diag(np.ones(n), 0)
+ np.diag(np.ones(n-1), -1)
)
# Truncate the matrices so that we only determine the derivative on the
# interior points (i.e. we don't calculate the derivative on the boundary)
return Dx[1:-1, :], Dxx[1:-1, :]
def perona_malik_smooth(p: np.array,
alpha: float = 10.0,
k: float = 0.05,
t_end: float = 5.0) -> np.array:
'''
Solve the Gaussian convolved Perona-Malik PDE using a basic finite
difference scheme.
Parameters
----------
p : np.array
The price array to smoothen.
alpha : float, optional
A parameter to control how much the PDE resembles the heat equation,
the perona malik PDE -> heat equation as alpha -> infinity
k : float, optional
The step size in time (keep < 0.1 for accuracy)
t_end : float, optional
When to termininate the algorithm the larger the t_end, the smoother
the series
Returns
-------
U : np.array
The Perona-Malik smoothened time series
'''
Dx, Dxx = get_diff_mat(p.shape[0])
U = deepcopy(p)
t = 0
while t < t_end:
# Find the convolution of U with the guassian, this ensures that the
# PDE problem is well posed
C = convolve_PDE(deepcopy(U))
# Determine the derivatives by using matrix multiplication
Cx = Dx@C
Cxx = Dxx@C
Ux = Dx@U
Uxx = Dxx@U
# Find the spatial component of the PDE
PDE_space = (
alpha*Uxx/(alpha + Cx**2)
- 2*alpha*Ux*Cx*Cxx/(alpha + Cx**2)**2
)
# Solve the PDE for the next time-step
U = np.hstack((
np.array([p[0]]),
U[1:-1] + k*PDE_space,
np.array([p[-1]]),
))
t += k
return U
因为使用了微分矩阵,所以基本上可以按照我们查看方程的格式中写出偏微分方程的离散形式。这使得调试比硬编码有限差分方程更简单。
但是这会不会引入数据泄漏?
如果平滑一个大的时间序列,然后将该序列分割成更小的部分,那么绝对会有数据泄漏。所以最好的方法是先切碎时间序列,然后平滑每个较小的序列。这样根本不会有数据泄露!
与热方程的比较
到目前为止,还没有说Perona-Malik PDE参数α。如果你取α非常大,趋于无穷,就可以将Perona-Malik PDE化简为热方程。
对于大的 α,基本上有一个扩散主导的机制,其中边缘保留是有限的。我们最终会得到这个方程组:

这里一维的热方程,以及问题的适当的初始/边界条件。用我们的微分矩阵法可以很好很容易地写他的代码:
def heat_smooth(p: np.array,
k: float = 0.05,
t_end: float = 5.0) -> np.array:
'''
Solve the heat equation using a basic finite difference approach.
Parameters
----------
p : np.array
The price array to smoothen.
k : float, optional
The step size in time (keep < 0.1 for accuracy)
t_end : float, optional
When to termininate the algorithm the larger the t_end, the smoother
the series
Returns
-------
U : np.array
The heat equation smoothened time series
'''
# Obtain the differentiation matrices
_, Dxx = get_diff_mat(p.shape[0])
U = deepcopy(p)
t = 0
while t < t_end:
U = np.hstack((
np.array([p[0]]),
U[1:-1] + k*Dxx@U,
np.array([p[-1]]),
))
t += k
return U
运行Perona-Malik PDE其中设α = 1,000,000,和热方程,基本得到了相同的结果。
最后让我们看看一些对比结果的动图
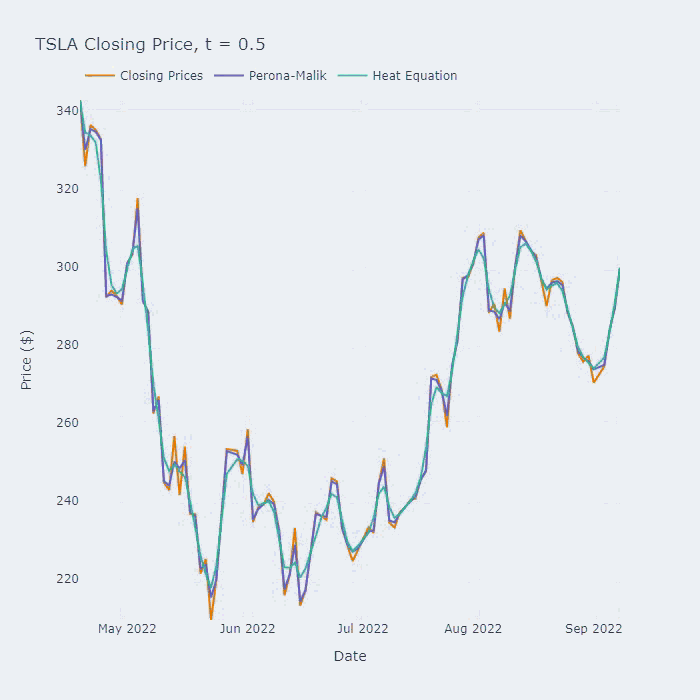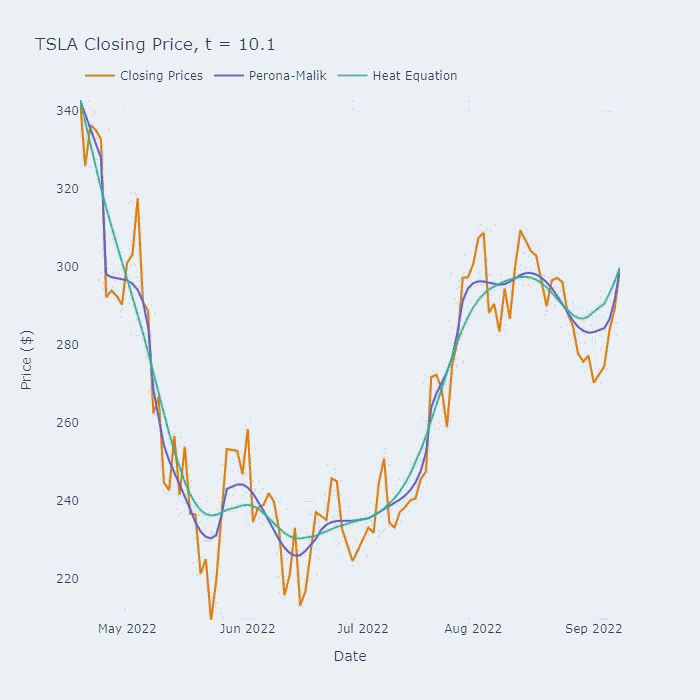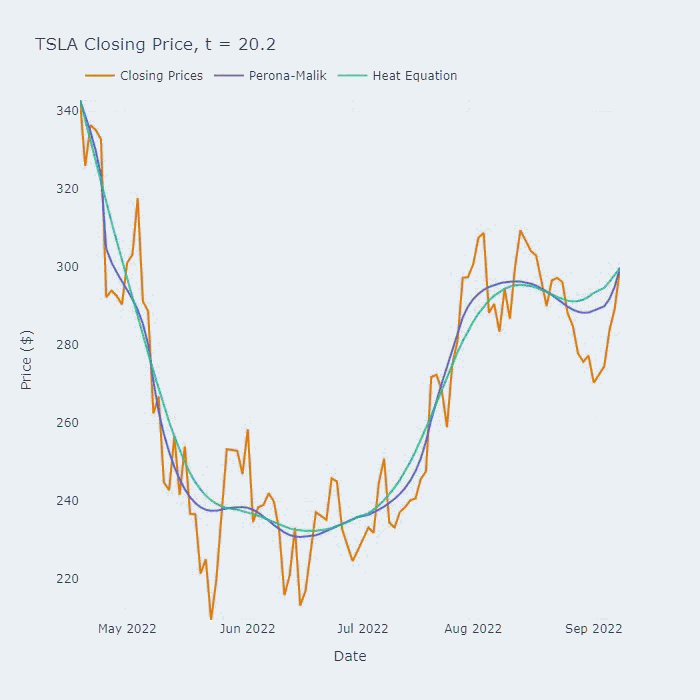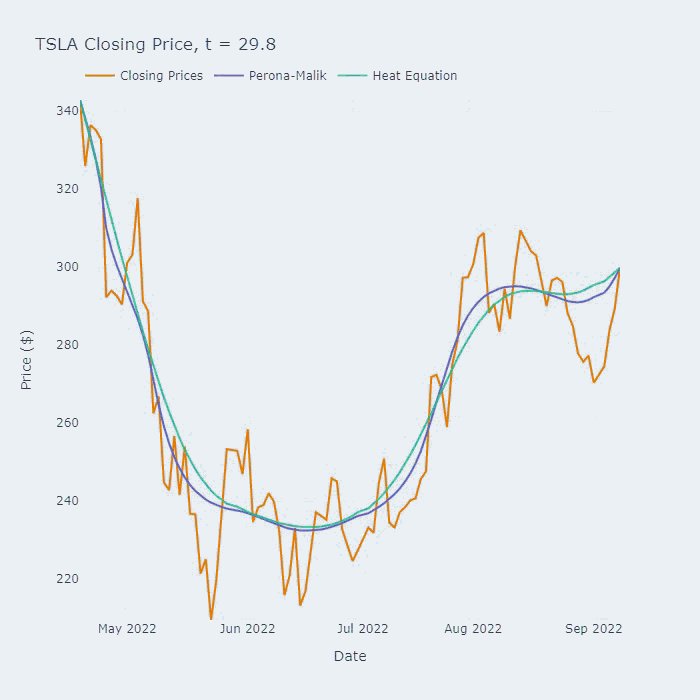
Perona-Malik PDE与热方程的比较。参数σ = 1, α = 20, k=0.05。
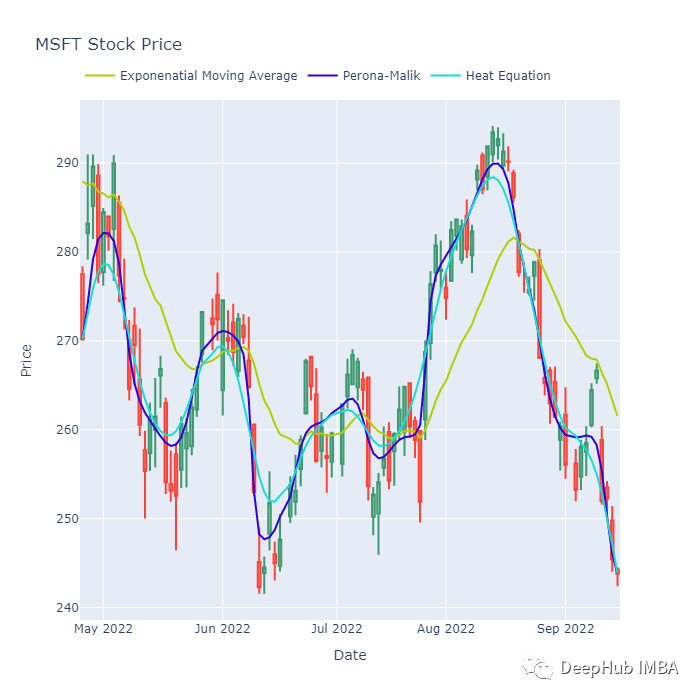
上图是比较Perona-Malik、热方程和指数移动平均方法对MSFT股价在2022年期间的时间序列数据进行平滑处理。
总结
总的来说,Perona-Malik 方法更好一些。虽然他的数学求解要复杂的多,但它确实对数据产生了非常好的结果。就个人而言,建议在开发过程中同时考虑 Perona Malik 和热方程方法,看看哪种方法可以为我们解决的问题提供更好的结果。




































