译者 | 李睿
审校 | 孙淑娟
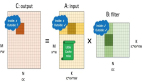
最佳运输源于经济学,如今被开发为如何最佳分配资源的工具。最优运输理论的起源可以追溯到1781年,当时的法国科学家加斯帕德·蒙格研究了一种据称“移动地球”的方法,并为拿破仑的军队建造防御工事。总体而言,最优运输是一个问题,即如何将所有资源(例如铁矿)从一组起点(矿场)移动到一组终点(钢铁厂),同时最小化资源必须移动的总距离。从数学上来说,研究人员希望找到一个函数,该函数将每个起点映射到一个目的地,同时最小化起点与其对应目的地之间的总距离。尽管其描述无伤大雅,但这一问题的原始构想(即蒙格构想)的进展仍停滞了将近200年。
在上世纪40年代,苏联数学家Leonid Kantorovich将该问题的构想调整为现代版本,即现在所称的Monge Kantorov理论,这是朝着解决方案迈出的第一步。这里的新奇之处在于允许来自同一矿山的一些铁矿提供给不同的钢铁厂。例如,一个矿山60%的铁矿可以提供给一家钢铁厂,而该矿山剩余40%的铁矿则可以提供给另一家钢铁厂。从数学上来说,这不再是一个函数,因为同一个原点现在映射到潜在的多个目的地。与其相反,这被称为起点分布和目的地分布之间的耦合,如下图所示;从蓝色分布(原点)中选择一个矿山,并沿着该图垂直移动,显示了铁矿被发送的钢铁厂(目的地)的分布。
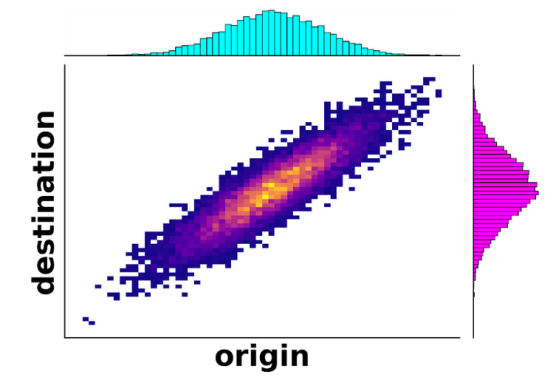
作为这一新发展的一部分,Kantorivich引入了一个重要的概念,称之为Wasserstein距离。与地图上两点之间的距离类似,Wasserstein距离(受其原始场景启发也称为推土机距离)测量两个分布之间的距离,例如本例中的蓝色和品红色分布。如果所有的铁矿都距离所有的铁厂都很远,那么矿山分布(位置)和钢铁厂分布之间的Wasserstein距离就会很大。即使有了这些新的改进,仍然不清楚是否真的存在运输铁矿资源的最佳方式,更不用说采用哪种方式了。最后在上世纪90年代,由于数学分析和优化的改进这一问题获得部分解决方案,该理论开始迅速发展。而进入21世纪,最优运输开始蔓延到其他领域,如粒子物理学、流体动力学,甚至统计和机器学习。
现代的最优运输
随着新理论的爆炸式发展,在过去二十年中,最优运输已成为许多新的统计和人工智能算法的中心。在几乎每个统计算法中,数据都被显式或隐式地建模为具有某种潜在的概率分布。例如,如果收集不同国家的个人收入数据,则该人口收入在每个国家都存在概率分布。如果希望根据人口的收入分布对两个国家进行比较,那么需要一种方法来衡量这两个分布之间的差距。这正是优化运输(尤其是Wasserstein距离)在数据科学中变得如此有用的原因。然而,Wasserstein距离并不是衡量两个概率分布相距距离的唯一指标。事实上,由于它们与物理学和信息论的联系,L-2距离和Kullback-Leibler(KL)散度这两种选择在历史上更为常见。Wasserstein距离相对于这些替代方案的主要优势在于,它在计算距离时同时考虑了值及其概率,而L-2距离和KL散度仅考虑概率。下图显示了一个关于三个虚构的国家收入的人工数据集的示例。
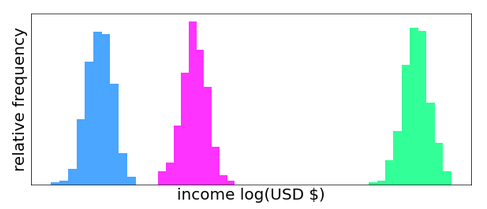
在这种情况下,由于分布不重叠,蓝色和品红色分布之间的L-2距离(或KL散度)将与蓝色和绿色分布之间的L-2距离大致相同。另一方面,蓝色和品红色分布之间的Wasserstein距离将远小于蓝色和绿色分布之间的Wasserstein距离,因为值之间存在显著差异(水平分离)。Wasserstein距离的这一特性使其非常适合量化分布之间的差异,特别是数据集之间的差异。
以最优运输实现公平
随着每天收集大量数据,机器学习在许多行业中变得越来越普遍,数据科学家必须越来越小心谨慎,不要让他们的分析和算法延续数据中现有的偏差和偏差永久化。例如,如果住房抵押贷款批准数据集包含关于申请者种族的信息,但由于使用的方法或无意识偏差,少数族裔在收集过程中受到歧视,则基于该数据训练的模型将在一定程度上反映潜在的偏差。
优化运输可以从两个方面帮助缓解这种偏差和提高公平性。第一种也是最简单的方法是使用Wasserstein距离来确定数据集中是否存在潜在偏差。例如,可以估计批准给女性的贷款金额分布和批准给男性的贷款金额分配之间的Wasserstein距离,如果Wasserstein距离非常大,即具有统计显著性,那么可能怀疑存在潜在偏差。这种测试两组之间是否存在差异的想法在统计学中被称为双样本假设检验。
或者,当底层数据集本身存在偏差时,甚至可以使用最优运输来强制模型中的公平性。从实际的角度来看,这非常有用,因为许多真实的数据集会表现出一定程度的偏差,并且收集无偏差的数据可能非常昂贵、耗时或不可行。因此,使用现有的数据更为实际,无论数据有多不完善,并尝试确保模型减轻这种偏差。这是通过在模型中强制实施称为强人口统计奇偶性的约束来实现的,该约束迫使模型预测在统计上独立于任何敏感属性。一种方法是将模型预测的分布映射到不依赖于敏感属性的调整预测的分布。然而,调整预测也会改变模型的性能和准确性,因此在模型性能和模型对敏感属性的依赖程度(即公平性)之间存在权衡。
通过尽可能少地更改预测以确保最佳模型性能,同时仍保证新预测独立于敏感属性,从而实现最佳运输。这种调整之后的模型预测的新分布被称为Wasserstein重心,在过去十年中一直是许多研究的主题。Wasserstein重心类似于概率分布的平均值,因为它最小化了从自身到所有其他分布的总距离。下图显示了三个分布(绿色、蓝色和品红色)以及它们的Wasserstein重心(红色)。
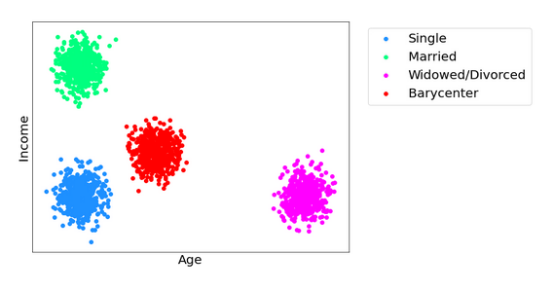
在上面的示例中,假设基于包含一个敏感属性(例如婚姻状况)的数据集构建了一个模型来预测某人的年龄和收入,该属性可以取三个可能的值:单身(蓝色)、已婚(绿色)和丧偶/离婚(品红色)。散点图显示了每个不同值的模型预测分布。但是希望调整这些值,以便新模型的预测对一个人的婚姻状况视而不见,可以使用最佳运输将这些分布中的每一个映射到红色的重心。因为所有值都映射到相同的分布,不能再根据收入和年龄来判断一个人的婚姻状况,反之亦然。重心尽可能地保留了模型的保真度。
企业和政府决策中使用的数据和机器学习模型越来越普遍,这导致了新的社会和道德问题的出现,即如何确保这些模型的公平应用。由于收集方式的性质,许多数据集包含某种偏差,因此在它们上训练的模型不会加剧这种偏差或任何历史歧视,这一点很重要。最优运输只是解决这一问题的一种方法,近年来这一问题一直在加剧。如今,有快速有效的方法来计算最佳运输地图和距离,使这种方法适用于现代大型数据集。随着人们越来越依赖基于数据的模型和洞察力,公平性已经并将继续成为数据科学的核心问题,而最佳运输将在实现这一目标方面发挥关键作用。
原文标题:Optimal Transport and its Applications to Fairness,作者:Terrence Alsup