介绍
让我们以一个例子来说明我们所面临的问题。想象一下,我们训练一个神经网络模型来预测包含汽车图像的概率。当我们使用这些概率来对有汽车的图像进行分类时,我们的模型有很好的准确性。在某些时候,我们给神经网络模型一个它从未见过的图像,例如企鹅。该模型表示,图像包含一辆汽车的概率为97%。基于这个例子,你会相信模型的预测吗?事实证明,这是神经网络的典型行为,因为企鹅与我们的训练数据相差太大。这种知道未知对象的能力是我们要寻找的,因为它在一些决策应用中是至关重要的,比如自动驾驶汽车。
什么是模型不确定性?
当我们谈论机器学习模型时,有两种类型的不确定性:
- 随机不确定性:它来自于数据生成过程中的随机性,例如,实验中的测量噪声。不管我们的模型有多好,这种不确定性都无法减少。
- 认知不确定性:它来自于知识的缺乏,这在机器学习中意味着要么我们没有足够的数据,要么我们的模型不够专业。如果我们获得了新知识,这种不确定性可以减少。
考虑到这一点,让我们看一下高斯过程给出的不确定性估计的具体例子。
高斯过程回归
高斯过程(GP)是贝叶斯机器学习模型。这意味着对于一个给定的数据输入点,我们将得到一个预测分布,而不是像我们在神经网络中得到的点估计。预测方差可以解释为不确定性的估计。
但是,这些模型是如何工作的呢?让我们想象我们有以下回归问题
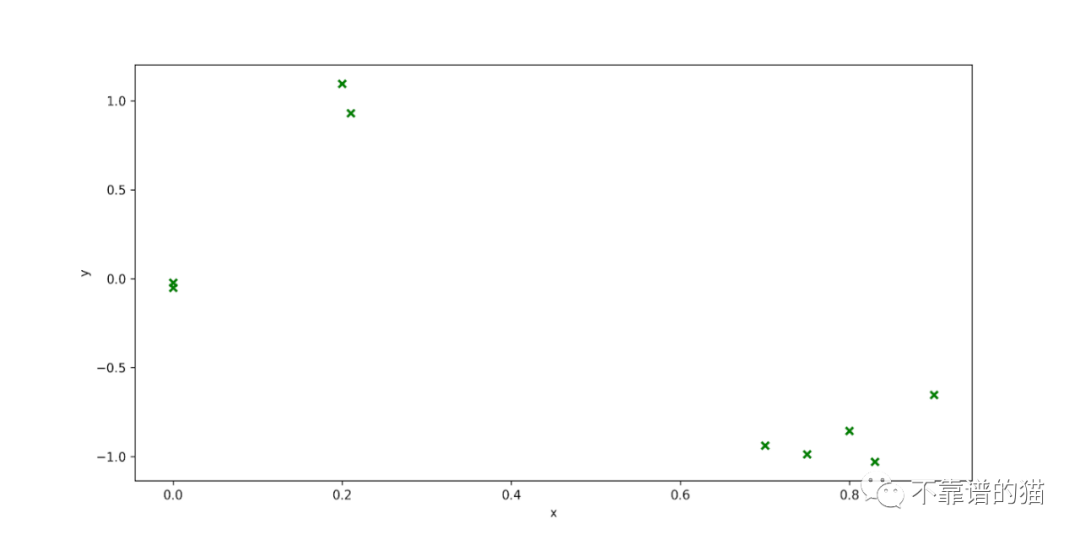
要解决的问题是找到更适合数据的函数。为此,我们假设观测y是产生数据的函数的噪声观测。也就是说,
y=f(x)+ϵ
其中, ϵ ∼ 𝒩(0, σ²)是加性高斯噪声,方差σ²对应于任意不确定性。
对于GP模型,我们假设生成数据的函数可以从高斯过程中得到,它可以被视为函数的分布。我们可以用均值函数m(x)和协方差函数k(x,x)来描述GP,即:
GP(m(x),k(x,x))
在实践中,我们在函数p(f) ~𝒩(0,k(x, x)) 上放置了一个 GP 先验,其中将均值函数设置为0以简化所需的计算而不损失通用性是一种常见的做法。这使得GP完全由其协方差函数或核来表征。核函数的选择将决定学习的函数的主要属性(平滑性、平稳性等)。常见的核选择是径向基函数或RBF核,它假定函数是平稳的。
如果我们使用贝叶斯规则将这些先验知识与观察到的数据结合起来,我们将获得函数值的后验分布。
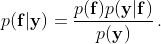
分母中有一个有趣的项,称为边际似然(marginal likelihood)或模型证据(model's evidence),它是一个归一化常数,可用于训练模型和寻找核函数的最佳参数。我们会得到满足给定属性并与数据兼容的函数。
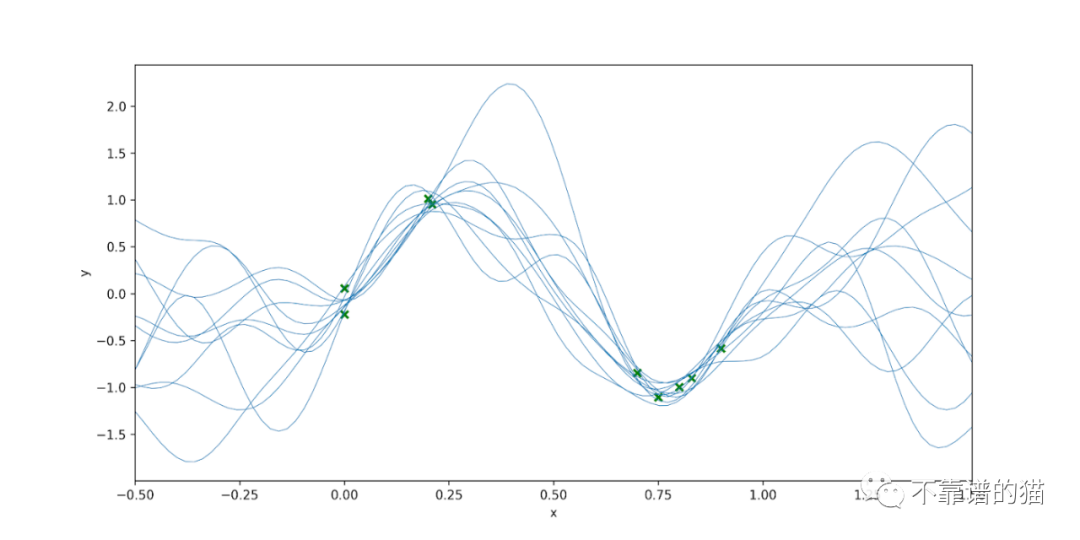
注意,在我们没有观察数据的区域,函数的可变性比我们有数据点的区域要高。有趣的是,我们可以利用这个后验得到一个预测分布来进行预测和相关的不确定性估计,最重要的是,这个分布可以以封闭形式计算。这里不会详细介绍,但它是均值和方差的高斯分布。这个问题的预测分布如下所示:
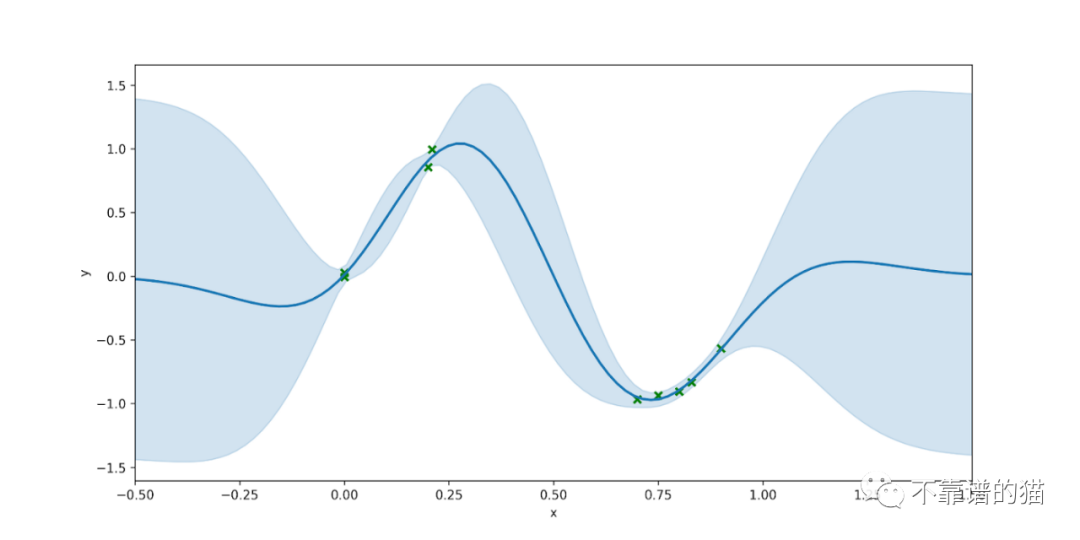
图中的蓝线代表预测的平均值,蓝色阴影区域代表预测方差或总不确定性。正如预期的那样,该模型对其在观测数据附近的预测更有信心,并且随着我们远离这些数据,不确定性将会增加。
如果您对实现感兴趣,这里是使用 Python 和 GPflow生成最后一个图形的代码:
import matplotlib.pyplot as plt
import numpy as np
import gpflow
# 生成数据的函数
def f(x):
return np.sin(2*np.pi*x)
# 我们生成一些假设高斯加性噪声的数据
X = np.array([0, 0, 0.2, 0.21, 0.7, 0.75, 0.8, 0.83, 0.9])
N = len(X)
epsilon = np.random.normal(scale=0.1, size=N)
y = f(X) + epsilon
X = X.reshape(-1, 1)
y = y.reshape(-1, 1)
# Plot the problem
plt.figure(figsize=(12, 6))
plt.plot(X, y, "kx", mew=2, c="g")
plt.xlabel("x")
plt.ylabel("y")
plt.savefig("problem.png", dpi=300)
# 定义核
kernel = gpflow.kernels.RBF()
# 构建模型
model = gpflow.models.GPR(data=(X, y), kernel=kernel, mean_function=None)
# Train the model
opt = gpflow.optimizers.Scipy()
opt.minimize(model.training_loss, model.trainable_variables)
# 生成用于预测的测试点
x_test = np.linspace(-0.5, 1.5, 100).reshape(100, 1) # test points must be of shape (N, D)
## predict mean and variance of latent GP at test points
mean, var = model.predict_f(x_test)
## 绘制预测
plt.figure(figsize=(12, 6))
plt.plot(X, y, "kx", mew=2, c="g")
plt.plot(x_test, mean, "C0", lw=2)
plt.fill_between(
xx[:, 0],
mean[:, 0] - 2 * np.sqrt(var[:, 0]),
mean[:, 0] + 2 * np.sqrt(var[:, 0]),
color="C0",
alpha=0.2,
)
_ = plt.xlim(-0.5, 1.5)
plt.xlabel("x")
plt.ylabel("y")
plt.show()
结论
在本文中,我们看到一些机器学习模型可能在训练数据之外给出过度自信的预测,这在实际应用中可能成为一个问题。我们还展示了高斯过程模型如何给不确定性进行估计。