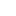The task of a zero-knowledge proof system is to "prove a fact without revealing knowledge."
Let's start with an image:

There are numerous penguins in it. However, a puffin looks like a penguin (below).

The situation is that you know where this puffin is hiding, but you don't want to tell others exactly where it is. What can you do to prove to others that you know the puffin's location without giving away the exact location?
A simple solution is to take a plastic plate, leave a hole in it, but the whole picture behind the plate, and let the puffin point at the hole.

As long as you look through the hole, you can see the puffin.

Looking back at the process, you can see that although you did not point out the exact location of the puffin, nor did you give any explicit or implicit information, the observer can be sure that there is a puffin in the picture, and would believe that you know the location.
This is so-called "zero-knowledge proof".
A strange definition of zero-knowledge
Zero-knowledge proof refers to the ability of a prover to convince a verifier that an assertion is correct without providing any valuable information to the verifier. It is essentially an agreement involving two or more parties, i.e., a series of steps that two or more parties need to take to accomplish a task. In short, a zero-knowledge proof system performs the task of "proving a fact and not revealing knowledge."
The official definition is a bit awkward, so let's take a classic example to illustrate it in layman's terms.
Suppose you have one red ball and one green ball in your hand, and you have a friend who has red-green color blindness. You cannot tell him what color the two balls are, but you must convince him that they are two different colors. What would you do in this situation?
Solution:
First, place two balls in each of his hands and ask him to remember the colors of the balls in his left and right hands.
Then, have him place his hands behind his back and randomly decide whether or not to switch the balls in his hands.
He will then show you the balls in his hands and ask you to judge whether or not they have been switched.
When comparing the colors of the balls, you can tell whether he switched them behind his back. Your friend knows the number of times the balls have switched and can demonstrate whether or not your estimation is accurate.
Additionally, to eliminate randomness, you can repeatedly conduct many trials.
As long as you continue to make accurate assessments, you may demonstrate that the two balls are distinct colors.
You (the prover) do not reveal any specific information about the colors of the balls to him (the verifier) throughout the entire process of proof, and your friend is unable to determine the colors of the balls on his own; therefore, no useful information about the proven message is transmitted, and he accepts the claim that "the two balls are different colors."
The study of zero-knowledge proof first began in 1985 with the paper "The Knowledge Complexity of Interactive Proof-Systems" by MIT professors Shafi Goldwasser, Silvio Micali, and cryptography guru Charles Rackoff. This paper introduced the concept of "zero-knowledge proof", which has gradually become one of the foundations of modern cryptographic theories.
A working zero-knowledge proof system must contain three properties.
Completeness: If both the prover and the verifier are honest, and the proof process conforms to the rules and is correct, then the proof must be successful, and the prover will eventually convince the verifier.
Soundness: Only the prover can make the proof, and the prover can only convince the verifier whether the statement is true or not, and there is no way for the prover to convince the verifier by fraud.
Zero-knowledge: After the proof process is performed, the verifier only gets the information that "the prover has this knowledge", but not the knowledge itself.
Application: from academia to blockchain
Initially, the research on zero-knowledge proof was mainly conducted in academia, and researchers focused on the cryptography of block cryptography, stream cryptography, and public-key systems. However, with the development of the Internet, especially mobile applications, a large amount of information involving privacy is stored, exchanged, and computed on connected devices, inevitably resulting in a large amount of privacy information leakage and the prevalence of Internet fraud.
With privacy and security being a primary concern today, zero-knowledge proof has greater use. For example,
Protecting private data: When buying insurance, you want to prove that you have no family medical history, and you don't want to expose all the information about your case. Regardless of the information, you can replace the part you don't want to reveal with a zero-knowledge proof that looks like a random number, proving that the data is accurate and trustworthy while protecting privacy.
Authentication: When using a website, a user can prove to the website that he has a private key or knows some answer that only he/she knows. The website does not have to know the key but can confirm the user's identity through zero-knowledge proof. The server can prove to the user that the data is properly preserved and not compromised based on decentralized storage.
Computation compression and blockchain scaling: In the traditional block architecture, the exact computation is repeated many times, such as signature verification, legitimacy verification of transactions, brilliant contract execution, etc. Because with proof of computation, the same computation does not need to be repeated many times, and the zero-knowledge proof technology can compress the computation process.
Recommendation of four mainstream zero-knowledge proof development libraries
Theoretically, any data stored today is bound to be leaked in the future, which is just a matter of time. All that can be done technically is to add difficulty to this data leakage so that it lacks immediacy and completeness when it is leaked, thus reducing its utilization value. For this aspect, a well-designed zero-knowledge protocol is a more promising solution. We recommend four mainstream zero-knowledge proof development libraries here and hope they will be helpful to readers.
libsnark: A zkSNARK scheme implementation developed by SCIPR Lab, developed in C++ and applied to several projects such as zcash.
snarkjs: A JavaScript implementation library for the zkSARNK scheme. With snarkjs you can perform trusted settings, generate evidence and verify the evidence.
bellman: A rust library for developing zk-SNARK circuits, which provides circuit interfaces, infrastructure, and basic circuit implementations such as Boolean and numerical abstractions.
pysnark: A zk-snark scheme implementation developed in Python that supports the Pinocchio protocol and supports the generation of smart contracts for Ethereum to verify zero-knowledge evidence.