译者 | 朱先忠
审校 | 孙淑娟

在我的印象中,在人工智能(AI)概念和工具的巨大空间中,生成性对抗网络(GANs)是作为一头未驯服的野兽站在一边。每个人都已经意识到它们的功能有多么强大;然而,很少有人知道如何训练它们,甚至很少有人能在实际任务中找到它们的用处。也许,我的观点是错误的;所以,请随意纠正我的观点中存在的问题。同时,我想再分析一下这种奇妙的机器模型,并想研究确定它是否能够适用于分类和嵌入方面的应用。为此,我们将执行以下几项计划:
- 就训练策略而言,更新我们有关GANs的知识和使用WGANs的论点
- 分析一个WGAN的自定义实现过程
- 在一组具有设计属性的对象上训练WGAN
- 使用经过训练的模型对另一组对象进行分类,看看我们是否可以解释这种分类
生成式对抗神经网络(GAN)概述
参考文献[1]中介绍了GAN有关知识,它们由两部分组成:鉴别器和生成器。其中,鉴别器就是一个能够接收对象输入并将其转换为数字型数据的函数。
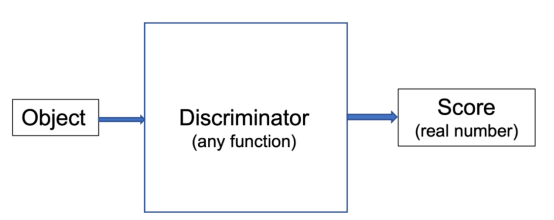
一个GAN的鉴别器部分的示意图
根据对象的复杂性,将其转换为数字可能是一项艰巨的任务。因此,我们可能会使用一个非常复杂的函数作为鉴别器,例如,深层卷积神经网络(CNN)。
在某种意义上,生成器执行相反的任务。它将一些随机数据作为输入,并从中生成一个对象。关于随机数据,我这里所指的是一些与我们的对象无关的随机数据。通常,它是从随机分布中提取的具有一定长度的向量。其中,向量长度和分布是固定的,就像在不可训练的模型参数中一样;但是,这实际上并不重要。
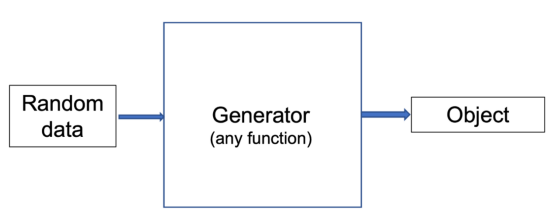
一个GAN的生成器部分的示意图
与鉴别器的情况一样,生成函数最好具有一定复杂性。通常,生成器和鉴别器具有类似的架构,我们稍后将在示例中看到这一点。
我故意用“对象”这个词而不是“图像”,因为我想让我们思考得更远。它可以是物理实体、过程或一条信息的任何数字表示。这里的关键是我们对特定类型的对象感兴趣,鉴别器和生成器处理相同类型的对象。所以,除了我们的模型、生成器+鉴别器外,我们必须拥有数据。这些数据给出了我们想要处理的对象的示例数据,我们的理想目标是教会模型识别这些对象。
训练过程是这样的。生成器开始生成对象,目标是生成与我们的数据集类似的内容。起初,这些物体看起来一点都不像。我们将它们输入鉴别器并收集得分,得分是指鉴别器的输出。此外,鉴别器对真实对象进行评分。在这里,生成器和鉴别器之间的对抗开始了,这也就自然地给这种方法起了“对抗”的名字。训练鉴别器以最大程度不同地对真实对象和生成的对象进行评分。生成器被训练为生成与真实对象非常相似的对象,以便鉴别器对其进行相似的评分。现在的诀窍是,将该策略转化为一个或两个待优化的目标函数。
WGAN训练方法
在机器学习中,鉴别器模型学习以数据为条件的概率,而生成器模型学习联合概率。就我个人而言,我目前还没有找到一个非常有说服力的关于这个主题的严格数学证明或全面的说明性讨论,以便为这一陈述提供良好的参考。然而,这在文献中被重复了很多次,我们现在可以认为这是理所当然的,特别是考虑到我们稍后将探索这一性质。
因为我们手上有一个生成器模型,所以我们先来学习一下全概率知识。在训练期间,我们需要衡量我们与真实事物的接近程度。当谈到比较概率时,会用到交叉熵和库尔巴克-莱布尔(Kullback-Leibler)散度等标准度量。假设我们想要量化两个分布p(x)和q(x)之间的差异,那么可以借助定义为以下内容的交叉熵来实现:
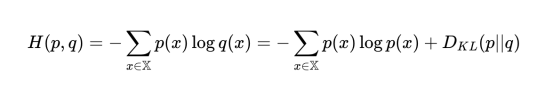
在上面表达式中,最后一项是Kullback-Leibler散度:

这一部分可以单独用作差异的度量。试验证明,当概率密度之间至少有一些重叠时,这种方法效果很好。
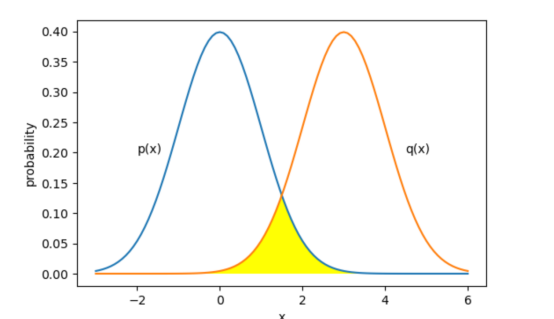
一种示例情形:可以通过交叉熵度量成功评估两个分布之间的差异
但如果分布距离太远时,上述这些度量措施就会失败。例如,下图中的情况看起来与交叉熵目标函数相同,但是不会产生有意义的定量。

交叉熵不起作用时的情况示例
但最重要的是,目标函数的优化基于梯度技术;当分布相距太远时,梯度将全部消失或未定义。我们的交叉熵目标函数不仅不能告诉我们有多远,甚至不能指示我们要往哪个方向走!
因此,参考文献[2]的作者提出了另外一种不同的测量方法——瓦瑟斯坦(Wasserstein)距离。用文字表示,它的定义类似于“将分布q(x)转换为p(x)所需的最小工作量”。也就是说,从字面上讲,如果我们的q(x)和p(x)是一堆土,那么将q(x)运输到p(x)所在的位置并从q(x)中构建与p(x)完全相同的土堆需要多少工作量。这乍听起来很好笑,但如果我们暂时忘记了所有需要用数学表达的麻烦,我们就会意识到这在概念上解决了我们的问题,因为它考虑了土堆的形状和它们之间的距离的差异。
那么,我们如何将过程定义转换为数学表达式呢?不幸的是,答案并不简单。我可以试着在这里画一个草图,但这个问题需要好几篇长度适中的博客来深入介绍所有有关细节。在参考文献[3]中可以找到一个关于这个主题的写得很好的博客。首先,要将我们对Wasserstein距离W(p,q)的措辞定义转换为类似于数学的东西,我们可以写成如下形式:
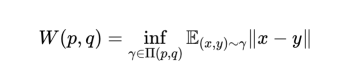
这里所指的是,我们正在寻找所有运输计划γ的最小值(inf),可以把运输所需的工作量定义成如下形式:
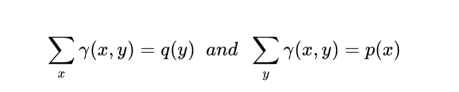
这里x是p(x)的支撑,代表p不为零的所有值(相应于p处垃圾堆的位置)。y是q(y)的支撑,即q不为零的值(相应于q垃圾堆的位置)。工作量被定义为质量块(密度γ)乘以需要传输的距离,即||x-y||。不过,这仍然没有多大帮助。但是,我们现在可以看到,这是一个优化问题。幸运的是,已经有一些人研究了类似的问题,并表明存在一个等价公式(Kantorovich-Rubinstein对偶),允许将我们的定义改写为:
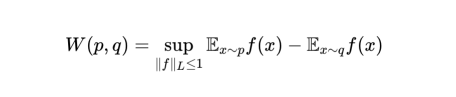
也就是说,我们现在正在寻找该表达式在所有函数上的最大值(sup),其增长受1约束(称为“Lipschitz约束”)。需要说明的是,这里跳过了几个步骤。您可以在参考文献[3]和其中的参考文献中找到这些更具体的被省略的步骤描述。而且,我也强烈建议您阅读一下有关瓦瑟斯坦距离的推导和有用属性的内容。但是,我们在这里仅对其进行直接规定。
我们可以说f(x)是我们的判别函数,并以最大化W(p,q)的最后一个表达式的方式训练模型。我们唯一要做的就是找出如何使函数f(x)满足Lipschitz约束。对此,参考文献[4]的作者建议施加梯度约束,使其接近1。这可以通过向W(p,q)添加惩罚项来实现:
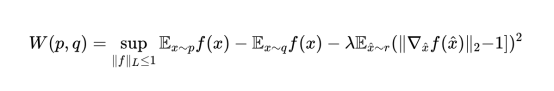
其中,梯度在x̂上计算,x是沿p和q之间的直线采样的点的子集。至此,一切准备就绪。接下来,我们要开发一个简单的实例来论证上面的结论。
构建模型
首先,让我们看看我通过下面的代码对WGAN的简单实现。
class WGAN_classic(tf.keras.Model):
def __init__(self, **kwargs):
super(WGAN_classic, self).__init__()
self.__dict__.update(kwargs)
self.gen = tf.keras.Model(inputs=self.gen.inputs,outputs=self.gen.outputs)
self.disc = tf.keras.Model(inputs=self.disc.inputs,outputs=self.disc.outputs)
def generate(self, z):
return self.gen(z)
def discriminate(self, x):
return self.disc(x)
def gradient_penalty(self, x, x_gen):
epsilon = tf.random.uniform([x.shape[0], 1, 1, 1], 0.0, 1.0)
x_hat = epsilon * x + (1 - epsilon) * x_gen
with tf.GradientTape() as t:
t.watch(x_hat)
d_hat = self.discriminate(x_hat)
gradients = t.gradient(d_hat, x_hat)
ddx = tf.sqrt(tf.reduce_sum(gradients ** 2, axis=[1, 2]))
d_regularizer = tf.reduce_mean((ddx - 1.0) ** 2)
return d_regularizer
@tf.function
def generator_train_step(self,x,step):
z_samp = tf.random.normal([x.shape[0], self.noise_dim])
with tf.GradientTape() as gen_tape:
x_gen = self.generate(z_samp)
logits_x_gen = self.discriminate(x_gen)
gen_loss = -tf.reduce_mean(logits_x_gen)
gen_gradients = gen_tape.gradient(gen_loss, self.gen.trainable_variables)
self.gen_optimizer.apply_gradients(
zip(gen_gradients, self.gen.trainable_variables))
return gen_loss
@tf.function
def discriminator_train_step(self,x,step):
z_samp = tf.random.normal([x.shape[0], self.noise_dim])
with tf.GradientTape() as disc_tape:
x_gen = self.generate(z_samp)
logits_x_gen = self.discriminate(x_gen)
logits_x = self.discriminate(x)
d_regularizer = self.gradient_penalty(x, x_gen)
disc_loss = (tf.reduce_mean(logits_x_gen)- tf.reduce_mean(logits_x)
+ d_regularizer * self.gradient_penalty_weight)
disc_gradients = disc_tape.gradient(disc_loss, self.disc.trainable_variables)
self.disc_optimizer.apply_gradients(
zip(disc_gradients, self.disc.trainable_variables))
return disc_loss, d_regularizer- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
该类扩展了Keras模型,并将生成器和鉴别器成员定义为Keras模型。生成器和鉴别器的实际结构必须在WGAN模型类之外构建。相反,类定义中实现了训练方法部分。
另外,需要分别对发生器和鉴别器进行训练。该模型为每个子任务定义了一个步骤。通常,对于生成器训练中的一个训练步骤对应于鉴别器训练中的多个训练步骤。生成器训练步骤只是最大化生成的伪对象的得分,或者更确切地说是最小化得分的负值。鉴别器训练步骤部分与我们上面引出的Wasserstein距离策略一致,最大化真实和虚假对象得分之间的差异;或者更确切地说,最小化差异的负值,同时考虑梯度惩罚。
以下是我在本文中构建的示例所使用的生成器和鉴别器函数的详细实现代码:
def RGenerator(input_z_shape=(NOISE_DIM)):
input_z_layer = tf.keras.layers.Input(input_z_shape)
output = tf.keras.layers.Dense(units=4 * 4 * 512)(input_z_layer)
output =tf.keras.layers.Reshape((4, 4, 512))(output)
output = residual_block(x=output, sampling=Sample.No,kernel_size=(4,4),filters=512)
output = residual_block(x=output, sampling=Sample.Up,kernel_size=(4,4),filters=256)
output = residual_block(x=output, sampling=Sample.Up,kernel_size=(4,4),filters=128)
output = residual_block(x=output, sampling=Sample.Up,kernel_size=(4,4),filters=64)
output = residual_block(x=output, sampling=Sample.Up,kernel_size=(4,4),filters=32)
output = tf.keras.layers.Conv2D(filters=3,kernel_size=(4,4),strides=1,padding="same")(output)
model = tf.keras.Model(inputs=input_z_layer, outputs=output)
return model
def RDiscriminator(input_x_shape=(IMG_W,IMG_H,3)):
input_x_layer = tf.keras.layers.Input(input_x_shape)
output = residual_block(x=input_x_layer,sampling=Sample.Down,kernel_size=(4,4),filters=32)
output = residual_block(x=output,sampling=Sample.Down,kernel_size=(4,4),filters=64)
output = residual_block(x=output,sampling=Sample.Down,kernel_size=(4,4),filters=128)
output = residual_block(x=output,sampling=Sample.Down,kernel_size=(4,4),filters=256)
output = residual_block(x=output,sampling=Sample.No,kernel_size=(4,4),filters=512)
output = tf.keras.layers.Conv2D(filters=1,kernel_size=(4,4),strides=1,padding="same")(output)
output = tf.keras.layers.Flatten()(output)
output = tf.keras.layers.Dense(1)(output)
model = tf.keras.Model(inputs=input_x_layer, outputs=output)
return model- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
注意到,它们都使用了所谓的残差块技巧;这种技术鼓励模型将注意力集中在拟合前一步不太合适的部分上,并能促进稳健收敛:
def residual_block_down(x, downsample:bool, kernel_size,filters):
y = tf.keras.layers.Conv2D(kernel_size=kernel_size,
strides= ((1,1) if not downsample else (2,2)),filters=filters,
padding="same",activation="relu")(x)
y = tf.keras.layers.Conv2D(kernel_size=kernel_size,
strides=(1,1),filters=filters,padding="same")(y)
x = tf.keras.layers.Conv2D(kernel_size=1,
strides=((1,1) if not downsample else (2,2)),filters=filters,padding="same")(x)
out = tf.keras.layers.Add()([x, y])
out = tf.keras.layers.ReLU()(out)
return out
def residual_block_up(x, kernel_size,filters):
x = tf.keras.layers.Conv2DTranspose(kernel_size=1,strides=2,filters=filters,padding="same")(x)
y = tf.keras.layers.Conv2D(kernel_size=kernel_size,
strides= (1,1),filters=filters,padding="same",
activation="relu")(x)
y = tf.keras.layers.Conv2D(kernel_size=kernel_size,
strides=(1,1),filters=filters, padding="same")(y)
out = tf.keras.layers.Add()([x, y])
out = tf.keras.layers.ReLU()(out)
return out
def residual_block(x,sampling:Sample,kernel_size,filters):
if sampling == Sample.Up:
return residual_block_up(x=x,kernel_size=kernel_size,filters=filters)
else:
return residual_block_down(x=x,downsample = sampling == Sample.Down,kernel_size=kernel_size,filters=filters)- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
我想指出的是,就本文而言,我们不需要完美的程序模型,我们只需要一个或多或少能起作用的模型就够了。稍后,我们将检查它是如何工作的,但现在我们先来看看训练集部分。
训练对象
对于训练对象,我创建了两类图像,都是3通道、64x64像素的图像。以下是生成它们的代码:
image_w = 64
image_h = 64
feature_size = min(image_w,image_h)*0.7
depth = 255
base_color = 0.7
noise_amp = 0.03
channel_offset = +1.
for i in range(num_images):
imageName = dir + 'square_' +str(base_color)+ "_" \
+ str(noise_amp)+"_" +str(channel_offset) + "_" + str(i) + '.png'
imageArray = np.full([image_h,image_w,3],255, 'uint8')
noise = np.random.normal(0, noise_amp, size=(image_h, image_w,3))
row_start = int((image_h - feature_size)/2)
row_end = image_h - row_start
col_start = int((image_w - feature_size)/2)
col_end = image_w - col_start
for i in range(col_start,col_end):
for j in range(row_start,row_end):
#circle
#r = math.sqrt((image_w/2 - i)*(image_w/2 - i) + (image_h/2 - j)*(image_h/2 - j))
#if r <= feature_size/2.:
imageArray[i,j,0] = (base_color + noise[i,j,0])*depth
imageArray[i,j,1] = (base_color + channel_offset*0.1 + noise[i,j,1])*depth
imageArray[i,j,2] = (base_color + channel_offset*0.2 + noise[i,j,2])*depth
img = Image.fromarray(imageArray)
img.save(imageName)- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
这是两种不同的形状——正方形和圆形,他们各自的颜色不同,如下图所示:

用于训练的两种类型的物体
对于第一个通道,归一化颜色定义为0到1之间的实数;在其他两个通道中偏移值分别为0.1和0.2。当然,偏移值的符号可以更改。在本例中,正方形使用的是符号“+”,而圆形使用的是“-”。颜色的生成方式没有特殊意义。我只是想有一个易于更改和记录的参数集合而已。这样,颜色被记录为一对(基色,偏移符号),因为它被标记在图片上。偏移值部分是固定不变的。此外,将预定义方差的随机正态噪声添加到每个通道。噪声的标准差是图像标签中的最后一个数字。
训练集中,每一种类型包含300个副本。由于随机噪声,同一类型的副本不完全相同。注意,这里添加噪声并不是某种正则化。相反,它仅仅意味着用于描述我们数据的真实连续特征。因此,我们提供了三个不同类型的特征:形状是明确指定的;颜色是半明确指定的,因为在数字图像中,存在许多级别,但颜色值仍然是离散的(每个级别中有3个通道乘以256个级别);噪声是连续的,由其方差定义。
开始训练
我对模型进行了最多200个阶段的8次批量训练。这次运行我将用于基准测试结果。下图显示了在训练迭代中鉴别器目标函数的值。
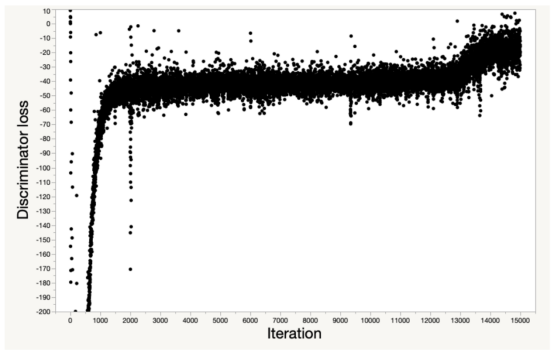
200次迭代训练期间鉴别器损失函数的轨迹图
上图中展示了我们所使用的Wasserstein距离,注意到它正朝着正确的方向发展,而且在最后1000次迭代中有一个明显的跳跃。我不知道为什么收敛不是更单调。但是,GAN是很复杂的技术,可能是由于我们的训练集有点过于人工给定的原因吧。总的来说,我们对这次训练很满意。
为了进一步检查,我在这里绘制了梯度惩罚项。它不完全为零,但它从上面就存在很好的边界,并且在不断下降。一切又好起来了。
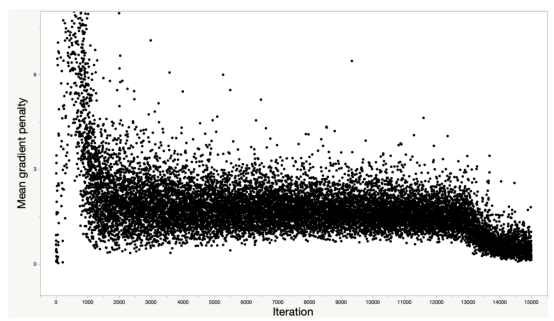
200迭代训练期间梯度惩罚项的轨迹图
现在,我们的模型已经训练到了合理的程度。接下来,我们将着手对其进行测试。
生成对象
在训练了GAN模型后,人们通常会丢弃其中的鉴别器部分,并使用生成器生成具有所需特性的新数据。我们也会这样做,但主要是作为另一次检查,证明训练效果良好。下面是我们训练模型生成的图像示例。它们大小相同,64x64,只是渲染得更小而已。

经过200次迭代训练后由模型生成的对象
可以看出,该模型已经掌握了一些诀窍——至少它没有生成猫的图像!而且,它的颜色是对的。这些形状虽然可以识别,但有时会混合在一起。一般来说,生成的数据质量还存在改进的潜力,但是目前这个模型正在开发中。接下来,让我们看看目前的结果是否足以达到我们的既定目的。
评分对象
现在,我们要开始做的是给模型从未见过的物体打分。我的实验目的自始至终就是想看一看经过训练的鉴别器最后的得分中是否存在任何模式。他们能否告诉我们模型从底层数据中学到了什么吗?
以下是鉴别器的测试集:
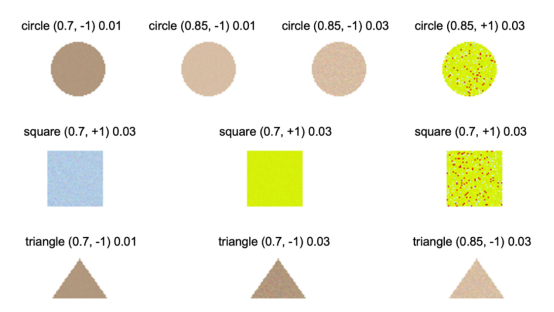
用于鉴别器测试的10类对象
注意到,我增加了更多的形状和颜色属性,但在其他方面,图像是在与上面相同的模式中生成的,大小相同,64x64。还有,新形状是一个三角形,两种新颜色(0.85,+1)和(0.7,-1)是通过切换偏移符号从旧颜色(0.85,-1)和(0.7,+1)创建的。总的来说,测试集中有10类对象,就我们的物体特征(形状、颜色和噪声)而言,其中两个与训练集中的相同。每个类型在测试集中有40个重复的。
我通过经过训练的鉴别器运行所有测试图像并收集得分。下面的表格总结了这一结果,并提供了下面的得分直方图的图例展示。以红色高亮显示的是用于训练的对象,以及模型以前未见过的其他对象。
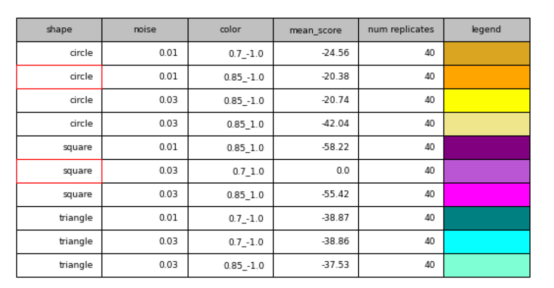
测试集中10个类型的得分汇总。图例颜色对应于下面的直方图图像
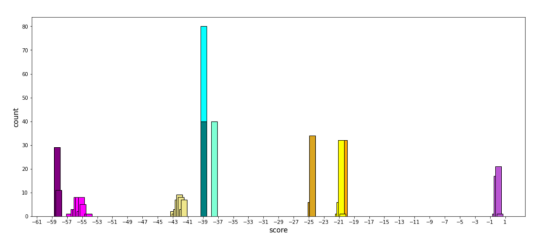
按对象类型着色的测试集的鉴别器得分直方图
令人惊讶的是,几乎所有测试的类型之间都有很好的分离。这说明该模型已经认识到它们属于不同的分布空间。
正如我所料,形状和颜色是模型最容易识别的特征,因为这些内容中不存在混乱。另外,新添加的形状三角形的得分与其他形状(中间的两个绿色条)良好地分离开来。即使在三角形形状内,该模型也能够通过颜色来分离对象。
噪声级别似乎是一个不太明显的特征。相同颜色的两个正方形被噪声很好地分开(见直方图上最左边的两组)。然而,相同颜色但不同噪声级的两个圆类型得分非常接近。尽管如此,如果我们放大得分分布,如下图所示,我们可以看到有微小但清晰的分离。如果我们对模型进行更长时间的训练,差距可能会扩大。
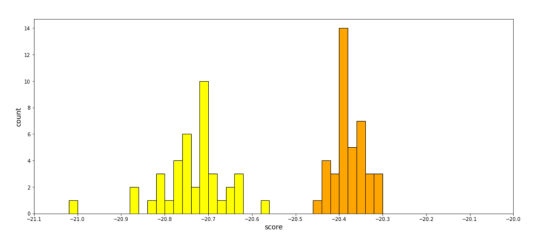
两个圆类型得分非常接近(亮黄色的“圆(0.85,-1)0.03”和深金色的“圆(0.85-1)0.01”),放大后的得分分布情况
到目前为止,唯一尚未解决的情况是两个颜色相同但噪声级不同的三角形。
所以,如果我们愿意,我们可以使用经过训练的鉴别器作为一个很好的分类器。这里我想提醒您的是,训练期间没有提供标签。该模型学会了将两个训练类型单独分开。此外,它还学会了正确区分从未见过的类型!
部分训练模型评分
在上面的情况中,我问自己一个问题:在训练过程中,得分的分离从多早开始?它与生成的图像的外观质量有何关系?为了回答这个问题,我对10、20和100个阶段的次优水平进行了训练。在每种情况下,训练都是从零开始的,而不是继续上一次训练。这可以导致得分的绝对值显示在不同的刻度上,但这也是我想要测试的一个方面。显而易见的预期结论是:得分的绝对值是没有意义的。
下图显示了该模型能够在左侧的每个训练级别生成的图像,以及由测试图像类型使用与上述相同的颜色方案着色的鉴别器得分的直方图。
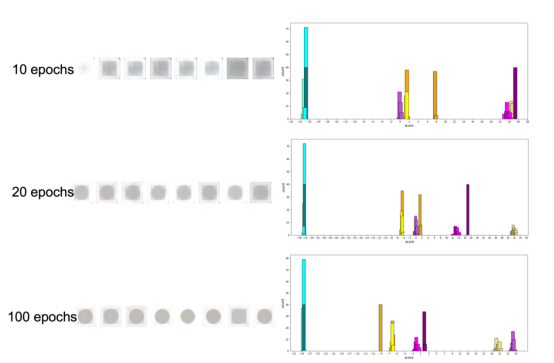
左侧为生成的对象,右侧为相应不同训练程度的测试对象的得分直方图
为了使它们更具可比性,我使用了“平方(0.85,+1)0.03”训练类型作为参考,并从所有得分中减去该类的平均得分。也就是说,“正方形(0.85,+1)0.03”类型的得分始终以0为中心。此外,相同形状的得分配色方案统一,以便于视觉比较。也就是说,直方图上的所有圆圈得分都是黄色,所有正方形都是紫色,所有三角形都是绿色。此外,得分颜色的强度与对象组的噪声级有关。越强烈、越暗的阴影表示噪声级越低,即0.01。具有讽刺意味的是,物体的实际颜色并没有进行颜色编码。
从这张图中可以明显看出,得分聚类在训练过程中很早就开始了。在仅仅10个迭代之后,训练显然不足以生成任何像样的图像。尽管如此,该模型已经对形状进行了不同的评分。经过20个阶段后,得分聚类变得更加精细,而数据生成仍不太顺利。值得一提的是,新的三角形形状在其他已经看到的形状之外一直得分很高。
所有这些都是从人类的角度进行的评估。不过,我们应该想知道机器是怎么想的。让我们在下一节中分析这个问题。
使用WGAN得分进行嵌入
使用经过适当训练的GAN模型的鉴别器部分作为分类器已经成为一种得到充分认可的策略了。我们可以更具创造性地将这些得分输入到另一个模型中,将它们与附加数据和元数据结合起来,以便进行一些复杂的分析。这种情况在机器学习中称为嵌入(embedding)。更准确地说,嵌入意味着,将一些不同的数据格式集或将高维数据减少为更易于计算的数据类型。例如,将表示文字形式的字符串转换为实数。
截止目前,我们已经对形状图像进行了处理,并为每个图像生成一个数字;但是,让我们更加挑剔一些,来分析一下这些数字是如何适合嵌入的。什么是良好的嵌入?我不知道这个问题有没有被普遍接受的答案,所以我将陈述我的观点。
数字的关键特征在于可比性,随之而来的是距离的概念。也就是说,如果你有两个数字,你可以判断它们是相同的还是不同的。在后一种情况下,通过多少来判断。我需要向早期的数学家们道歉,因为他们使用了一种平庸的语言。在当时,他们便开始讨论场和流形以及其中定义的测度等问题。
当我们将一个看似不可比的对象转换为数字时,我们自动获得了可比性的额外好处。当我们进行进一步分析时,这可能是一把双刃剑。一方面,机器可能会发现一些我们错过的模式;另一方面,它可能将有意义的东西转化为没有任何意义的东西。单词嵌入方面的一个著名例子是,你可以对嵌入的单词进行算术运算,并直观地获得正确的结果,例如,king-man+woman=queen,这就是一个很好的嵌入示例。
然而,我怀疑,由于人们只使用这个特定的例子,在自然语言处理(NLP)的同一领域中还存在许多其他情况,其中赋予了不直观的含义或丢失任何直观的含义。总之,在我看来,一个好的嵌入应该能够a)以某种逻辑方式对对象进行聚类;b)定义对象之间的距离,以便进行解释;c)做到始终如一。
我们的得分是多少?实验表明,我们的设计十分符合这里的条目a),因为我们清楚地观察到一些有意义的分组。让我们研究一下该模型提出的几个定量比较。根据得分之间的差异,机器将“圆(0.85,+1)0.03”和“正方形(0.7,+1)0.03”对象排列在相对于“三角形(0.7,-1)0.01”的这些位置。

不同测试类型的相对得分情况
如果让我猜测的话,我会说这里的决定因素可能是面积,这是形状属性量化的一部分。在另一个示例中,不同颜色和噪音的圆放置在以下图示的距离:

不同测试类别的相对得分情况
这可以很好地解释为颜色是主要考虑因素。还有另一个有趣的观察结果:得分分布的宽度似乎与图像组噪声水平有关。这可以解释为颜色和噪声特征之间相互作用的度量。在任何情况下,也可能满足上面的条目b)。但是,如果部分训练模型的结果有任何迹象,那么c)项是我们方法中最薄弱的部分。每次我们重新训练模型时,类型的相对得分都会不同。
我在文章的这个最后一节中讨论的大多是定性思考,尽管它们与定量估计有关。现在,我还没有对嵌入应用程序进行全面的研究。到目前为止,对于我们的鉴别器是否产生了适合嵌入的得分这一问题的答案可能是“否”,而不是目前的形式。
总论
总而言之,在本文中我们首先学习了生成性对抗神经网络GAN的基本原则。然后,我们回顾了在训练时使用瓦瑟斯坦(Wasserstein)距离作为目标函数的观点。所有这些都已成功地应用于演示GAN基于给定玩具数据集的内部工作原理。但是,这篇文章的主要目的却是让人们能够充分注意到GAN中被低估的部分——鉴别器。我希望我能够说服读者:鉴别器在一个GAN网络的幕后的确做了一些精彩的工作。最后,现在是时候让GAN在机器学习世界中扮演更重要的角色了。
引用文献
[1] I. J. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, Y. Bengio (2014), Generative Adversarial Networks, arXiv:1406.2661
[2] M. Arjovsky, S. Chintala, and L. Bottou, Wasserstein GAN (2017), arXiv:1701.07875
[3] V. Herrmann, Wasserstein GAN and the Kantorovich-Rubinstein Duality
[4] I. Gulrajani, F. Ahmed, M. Arjovsky, V. Dumoulin, A. Courville, Improved Training of Wasserstein GNAs (2017) arXiv:1704.00028
译者介绍
朱先忠,51CTO社区编辑,51CTO专家博客、讲师,潍坊一所高校计算机教师,自由编程界老兵一枚。早期专注各种微软技术(编著成ASP.NET AJX、Cocos 2d-X相关三本技术图书),近十多年投身于开源世界(熟悉流行全栈Web开发技术),了解基于OneNet/AliOS+Arduino/ESP32/树莓派等物联网开发技术与Scala+Hadoop+Spark+Flink等大数据开发技术。
原文标题:Unsupervised Classification with Generative Models,作者:Svetlana Rakhmanova Shchegrova