用栈实现队列 & 用队列实现栈-两个栈实现队列

栈和队列

栈和队列都是一种数据结构，它们的作用都是存储。

每种数据结构都有着其对应的特性。队列的特性是先进先出，而栈的特性是先进后出：

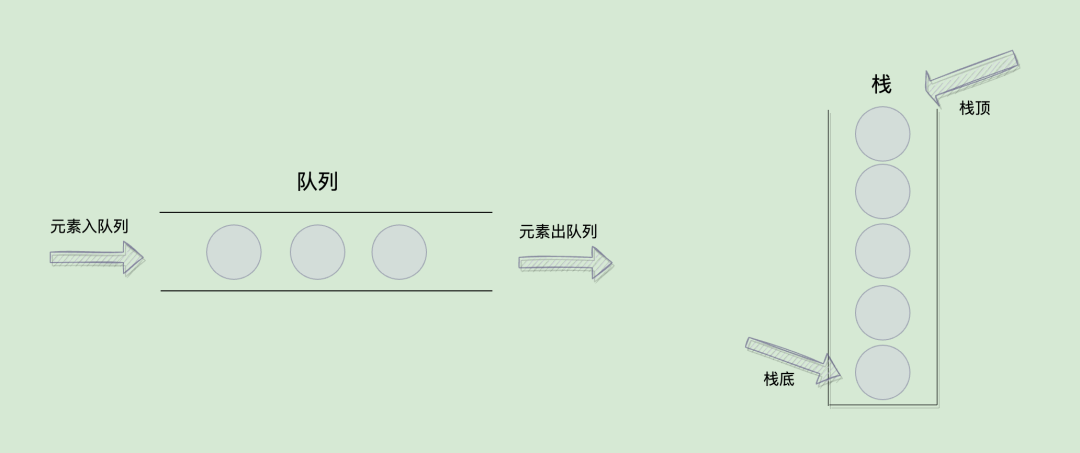
只有满足了它们的以上特性，一个数据结构才能被称为栈或者队列。

接下来我们看一下这两道经典的数据结构设计题：

用栈实现队列

要用栈实现队列，就得实现队列的以下API：

void push(int x) // 将元素添加到队列的尾处
int pop() //删除队列的头部元素并且返回
int peek() //返回队列的头个元素
boolean empty() //判断队列是否为空

我们要让设计的队列满足以上API的使用。

队列有队列头部和队列尾部。所以我们可以用两个栈，通过栈的特性让它们相互配合从而实现一个队列：

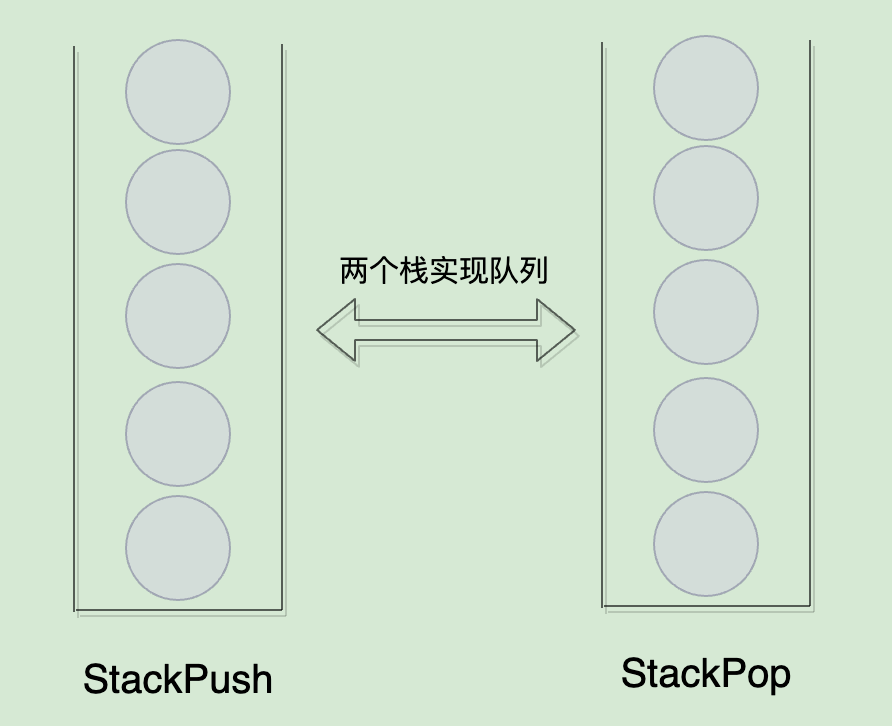
    Stack<Integer> stackPush;  //一个栈用来负责push元素
    Stack<Integer> stackPop; //一个栈用来负责将元素pop掉

    //初始化
    public MyQueue() {
        stackPush = new Stack<Integer>();
        stackPop = new Stack<Integer>();
    }

push():

push()要做的，就是将一个元素添加到队列的尾处。

所以这里我们可以直接调用栈的push()，然后把元素打入stachPush这个栈就好了：

    public void push(int x) {
        stackPush.push(x);
    }

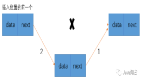
此时，元素1就在stachPush这个栈的底部：

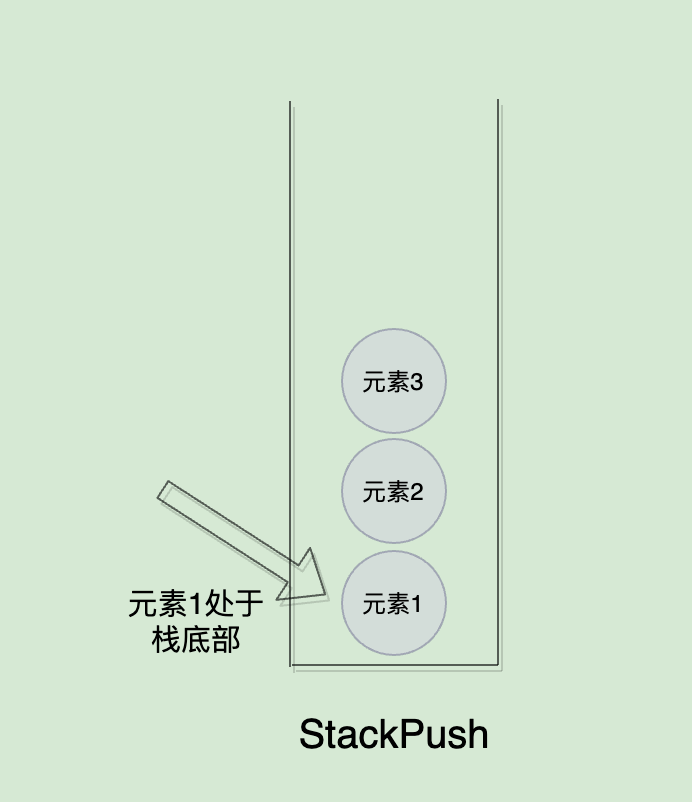
pop():

pop()就是删除队列的头部元素并且返回。

有了刚才push()的经验，pop()依然可以按照push()刚才经验，就是当stackPop为空的时候，按顺序把stackPush里面的元素一个一个pop()掉，并且返回给stackPop：

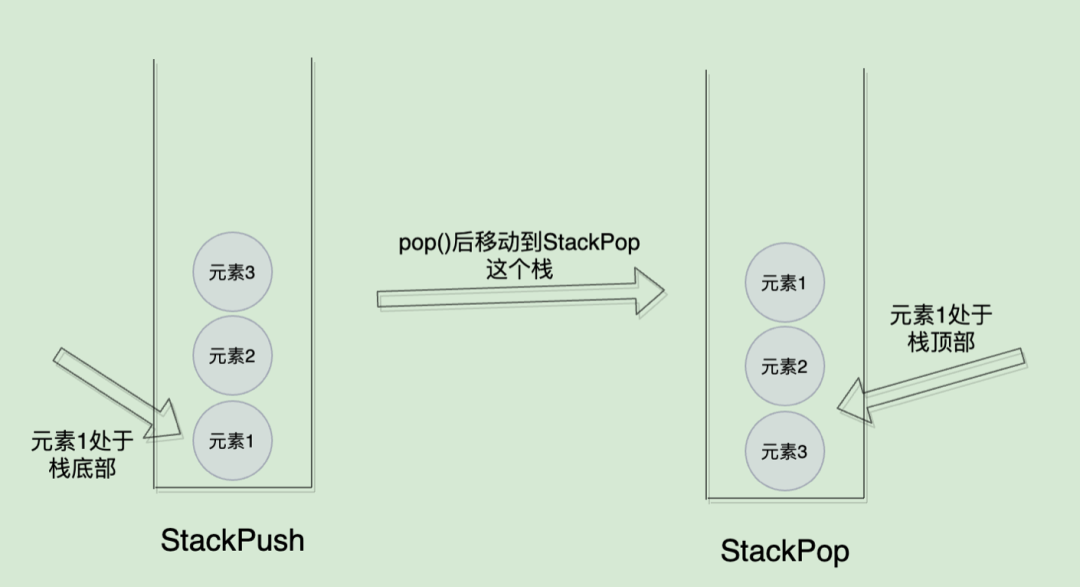
然后再将stackPop()里面的元素pop()返回：

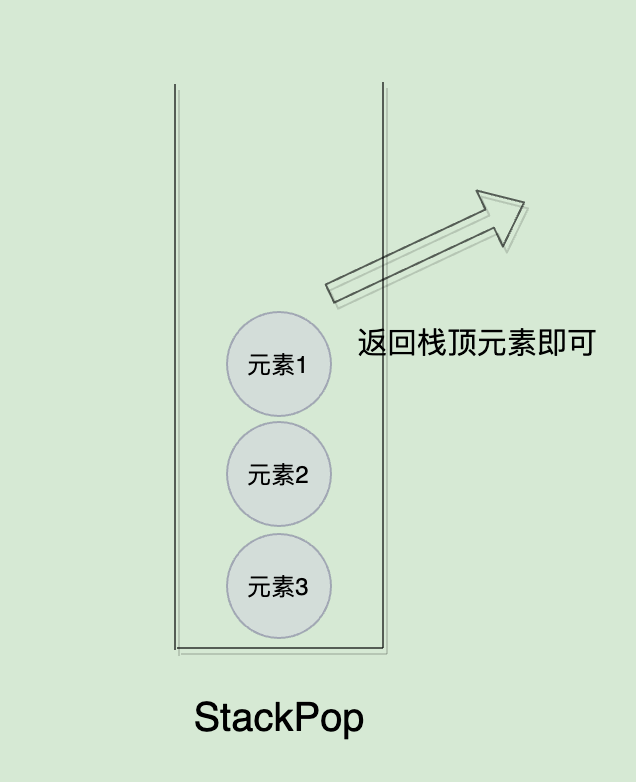
    public int pop() {
        if (stackPop.isEmpty() && stackPush.isEmpty()) {
            throw new RuntimeException("Queue is empty.");
        } else {
            if (stackPop.isEmpty()) {
                while (!stackPush.isEmpty()) {
                    stackPop.push(stackPush.pop());
                }
            }
        }
        return stackPop.pop();
    }

peek()：

peek就是返回队列的头个元素：

pop()和peek()的区别是什么呢？就是pop()返回队列头个元素并且要删除，但是peek()返回却不删除呀。

所以，和pop()的思路一样，只需要在最后返回的时候把stackPop.pop()换成stackPop.peek()就完事了。

    public int peek() {
        if (stackPush.isEmpty() && stackPop.isEmpty()) {
            throw new RuntimeException("Queue is empyt.");
        } else {
            if (stackPop.isEmpty()) {
                while (!stackPush.isEmpty()) {
                    stackPop.push(stackPush.pop());
                }
            }
        }
        return stackPop.peek();
    }

empty()：

判断队列是否为空，为空就返回true，不为空就返回false。

所以我们也可以直接判断两个栈是否同时为空。只要同时为空就返回true，不同时为空就返回false：

    public boolean empty() {
        return stackPop.isEmpty() && stackPush.isEmpty();
    }

可以看出，用栈实现队列思路还是比较简单的。主要利用的是两个栈的相互配合。其核心思路就是一个数据从一个栈的队尾移动到另一个栈，就处于队头的位置。

那么来说一下时间复杂度，当队列为空的时候pop()和peek()都要通过while循环把元素从stackPush移动到stackPop，所以复杂度是O(n)。

用队列实现栈

先看看栈的API：

void push(int x) //将元素压入栈顶
int pop() //移除并返回栈顶元素
int top() //返回栈顶元素
boolean empty() //如果栈是空的，返回 true ；否则，返回 false 。

和队列的API一样。只不过这一次我们是要模拟由队列实现栈。

如果说用栈实现队列是一种相互配合的方式的话，那么由队列实现栈就不需要了。我们可以使用ArrayDeque()来实现队列。

    Queue<Integer> queue;
    // 使用ArrayDeque作为队列
    public MyStack() {
        queue = new ArrayDeque<>();
    }

push(int x)：

根据栈的特性，第一个入栈的元素会处于栈底部。所以在使用队列模拟栈的时候，可以先把元素入队列，然后再一个一个拿出来，最后再入一次队列，这样子原本处于队列头的元素就到了队列尾部，相当于栈头：

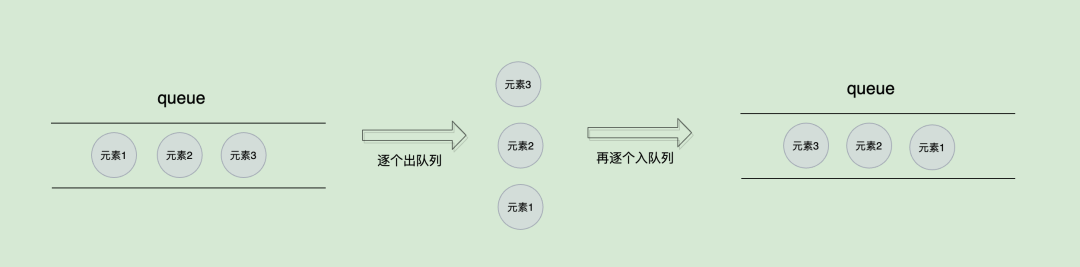
    // 入栈时，将新元素x进入队列后，将新元素x之前的所有元素重新入队，此时元素x处于队头
    public void push(int x) {
        queue.offer(x);
        int size = queue.size();
        for (int i = 0; i < size - 1; i++) {
            queue.offer(queue.poll());
        }
    }

pop():

由于出栈的操作是和出队列的操作是相同的，当我们把元素从队列头变到队列尾部后，就直接poll()出来即可：

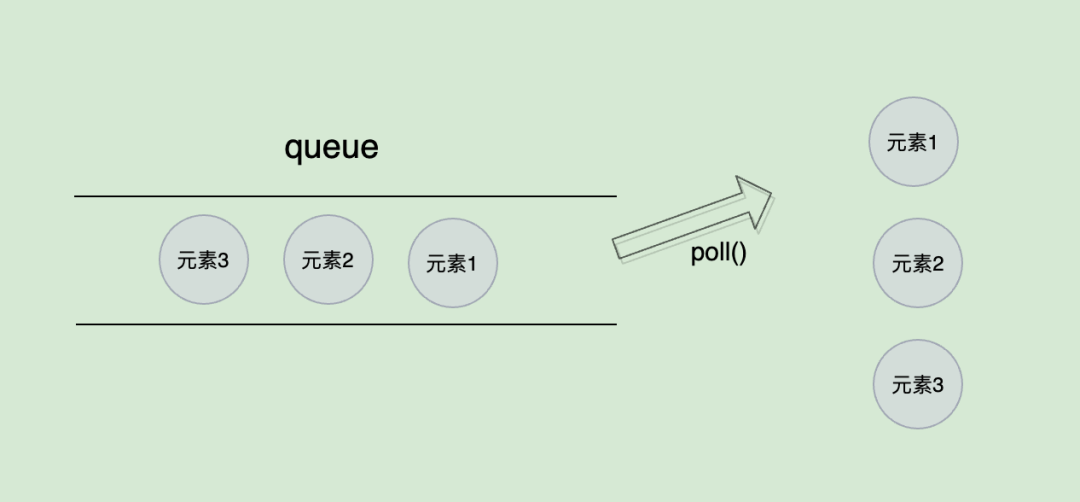
    public int pop() {
        if (queue.isEmpty()) {
            throw new RuntimeException("EMPTY STACK");
        }
        return queue.poll();
    }

top() ：

获取栈头部元素，就相当于队列的peek():

    public int top() {
        if (queue.isEmpty()) {
            throw new RuntimeException("EMPTY STACK");
        }
        return queue.peek();
    }

empty():

返回队列是否为空，都是通用的：

    public boolean empty() {
        return queue.isEmpty();
    }

相比于用栈实现队列，用队列实现栈就非常简单。核心思想就是将队列的元素先拿出来再放进去从而满足先进后出的特性。

那么它们的时间复杂度是多少呢？其它操作都是O(1)。只有pop()操作需要通过循环把元素从队列拿出来再放进去，所以时间复杂度是O(n)。

以上就是用栈实现队列 & 用队列实现栈的思路。主要是用来考察栈和队列的特性。