译者 | 朱先忠
审校 | 孙淑娟
引言
在许多情况下,我们不仅对估计因果效应感兴趣,而且对不同用户的这种效应是否不同也感兴趣。我们可能有兴趣了解一种药物是否对不同年龄的人有不同的副作用。或者,我们可能有兴趣了解广告活动是否在某些地理区域特别有效。
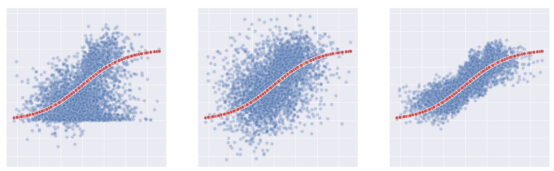
这一知识至关重要,因为它使我们能够实施针对性治疗。如果一种药物对儿童有严重的副作用,我们可能希望限制其使用人群仅向成年人销售。或者,如果一个广告活动只在英语国家有效,那么它就不值得在其他地方展示。
在本文中,我们将探计利用机器学习算法揭示治疗效果异质性的一些方法。
案例分析
假设我们是一家公司,有兴趣了解新的保险功能能够在多大程度上增加用户收入。特别是,我们知道不同年龄段的用户有不同的消费态度,我们怀疑保险功能的影响也可能因用户年龄而异。
这些信息可能非常重要,例如对于像广告定位或折扣设计这样的应用尤其如此。如果我们发现保险功能增加了特定用户群的收入,我们可能希望针对该用户群的广告或为他们提供个性化折扣。
为了了解保险功能对收入的影响,进行了AB测试。在该测试中,我们随机向测试样本中10%的用户提供保险功能的访问权限。这项功能很昂贵,我们负担不起将其免费提供给更多用户。因此,我们希望能够达到10%的治疗概率就足够了。
我们选择使用src.dgp库提供的数据生成过程dgp_premium()函数来生成试验中所需要的模拟数据。此外,我们还要从src.utils库导入一些必要的绘图函数和库。
from src.utils import *
from src.dgp import dgp_premiumdgp = dgp_premium()
df = dgp.generate_data(seed=5)
df.head()
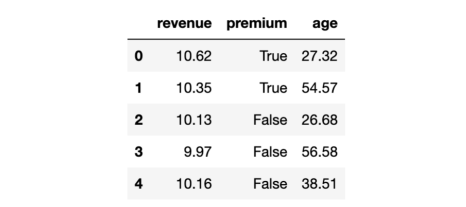
数据快照
实验中,我们采集了300名用户的数据,我们观察他们产生的收入,以及他们是否获得了医疗保险功能。此外,我们还记录了这些用户的年龄。
为了了解随机化是否有效,我们使用美国Uber公司的causalml软件包中的create_table_one函数生成了一个协变量平衡表,其中包含实验组和对照组的可观察特征的平均值。顾名思义,这应该始终是您在因果推理分析中呈现的第一个表。
from causalml.match import create_table_one
create_table_one(df, 'premium', ['age', 'revenue'])
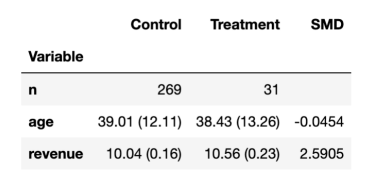
平衡表
由上表可见,大多数用户都出现在对照组中,只有31个用户位于实验组中。不同组的平均年龄具有可比性(标准化平均差,SMD<0.1),而且看起来保险功能平均为每个用户增加了2.59美元的收入。
那么,保险功能的效果是否因用户年龄而异?
一种简单的方法是,在保险功能和年龄的充分交互作用下对收入进行回归分析。
linear_model = smf.ols('revenue ~ premium * age', data=df).fit()
linear_model.summary().tables[1]
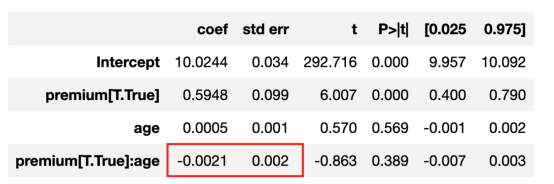
线性回归结果
从上述分析结果看出,交互作用系数接近零且不显著。似乎保险费方面不存在年龄差异效应。但事实上,这是真的吗?因为交互作用系数仅捕捉线性关系。如果这种关系是非线性的呢?
我们可以通过直接绘制原始数据进行检查。我们按年龄划分收入,将数据分为保险用户和非保险用户。
sns.scatterplot(data=df, x='age', y='revenue', hue='premium', s=40);
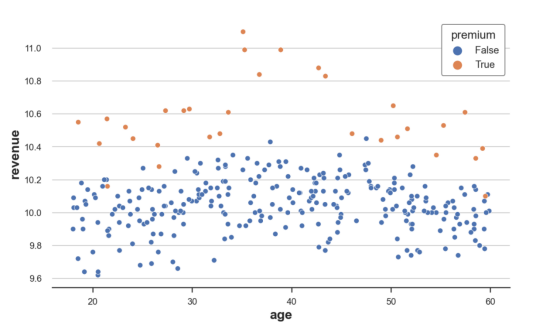
原始图像
从原始数据来看,30岁至50岁的人的收入通常较高,而保险费对35岁至45岁的人的影响尤为显著。
我们可以按年龄将估计的收入值加以可视化,其中包括治疗和不治疗两种类型。
def plot_TE(df, true_te=False):
sns.scatterplot(data=df, x='age', y='revenue', hue='premium', s=40, legend=True)
sns.lineplot(df['age'], df['mu0_hat'], label='$\mu_0$')
sns.lineplot(df['age'], df['mu1_hat'], label='$\mu_1$')
if true_te:
plt.fill_between(df['age'], df['y0'], df['y0'] + df['y1'], color='grey', alpha=0.2, label="True TE")
plt.title('Distribution of revenue by age and premium status')
plt.legend(title='Treated')
我们首先用(μ̂₁)计算预测收入;注意,我们并没有使用保险特征(μ̂₀)。然后,将它们与原始数据一起绘制出来。
df['mu0_hat'] = linear_model.predict(df.assign(premium=0))
df['mu1_hat'] = linear_model.predict(df.assign(premium=1))
plot_TE(df)
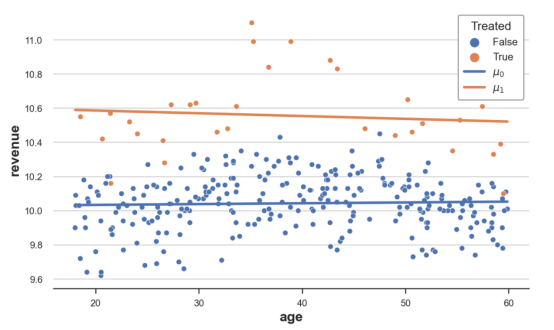
显示有原始数据的线性估计结果
正如我们从上图中观察到的,橙色线高于蓝色线,这表明保费对收入有积极影响。然而,这两条线基本上是平行的,表明实验效果没有异质性。
我们能否更精确一点?有没有一种方法可以在没有假设使用功能形式的情况下,以灵活的方式估计这种治疗异质性?
答案是肯定的!我们可以使用机器学习方法灵活地估计异质治疗效果。具体地说,我们将从现在开始细致分析Künzel、Sekhon、Bickel和Yu(2019年论文,详见https://www.pnas.org/doi/abs/10.1073/pnas.1804597116)介绍的下面三种流行方法:
- n S-learner
- n T-learner
- n X-learner
初始设置
我们假设有这样一组接受试验者i=1,…,n,我们要观察一个元组(Xᵢ, Dᵢ, Yᵢ)。其中:
- 实验任务Dᵢ∈{0,1} (保费)
- 响应 Yᵢ∈ℝ (收入)
- 特征向量 Xᵢ∈ℝⁿ (年龄)
我们对估计平均实验效果感兴趣。
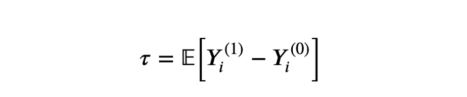
平均实验效果
其中,Yᵢ⁽ᵈ⁾表明个体i在实验状态d下的潜在结果。我们还做出以下假设:
假设1:无根据性(或可忽略性,或对可观察项的选择)
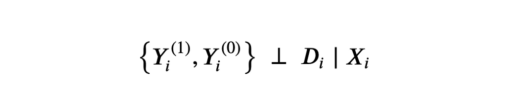
无根据假设
也就是,以可观察特征X为条件,实验任务D与随机分配一样好。我们实际上假设的是,不存在我们观察不到的情形——此情形下可能影响用户是否获得保险特征和收入特征。这是一个强有力的假设,我们观察到的个性化特征越多,就越有可能得到满足。
假设2:稳定的单位治疗费用(SUTVA)
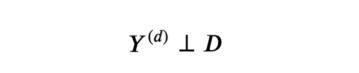
SUTVA假设
也就是,潜在结果不取决于实验状态。在我们的案例中,我们排除了另一个用户获得保险功能可能会影响我的保险对收入的影响这一事实。违反上述SUTVA假设的一种最常见情形是存在网络影响:例如,我的一个朋友通过社交网络增加了我的就医费用。
S-Learner方案
最简单的元算法是单学习器(single learner)或S学习器(S-learner)。为了构建S-learner估计量,我们为所有观察值拟合一个模型μ。
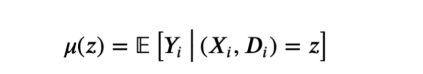
S-learner响应函数
估计量由经过和未经处理的预测值之间的差值得出,分别为d=1和d=0。
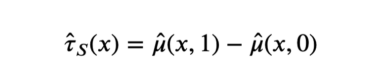
S-learner估计量
def S_learner(dgp, model, y, D, X):
temp = dgp.generate_data(true_te=True).sort_values(X)
mu = model.fit(temp[X + [D]], temp[y])
temp['mu0_hat'] = mu.predict(temp[X + [D]].assign(premium=0))
temp['mu1_hat'] = mu.predict(temp[X + [D]].assign(premium=1))
plot_TE(temp, true_te=True)
让我们使用sklearn包中的DecisionTreeRegressor函数,并使用决策树回归模型来构建s-learner。篇幅所限,我不会在这里详细介绍决策树信息;仅说明下决策树是一种非参数估计量,它使用训练数据将状态空间(在我们的例子中是保费和年龄)分割成块,并预测结果(在我们的例子中是收入)作为其在每个块中的平均值。
from sklearn.tree import DecisionTreeRegressor
model = DecisionTreeRegressor(min_impurity_decrease=0.001)
S_learner(dgp, model, y="revenue", D="premium", X=["age"])
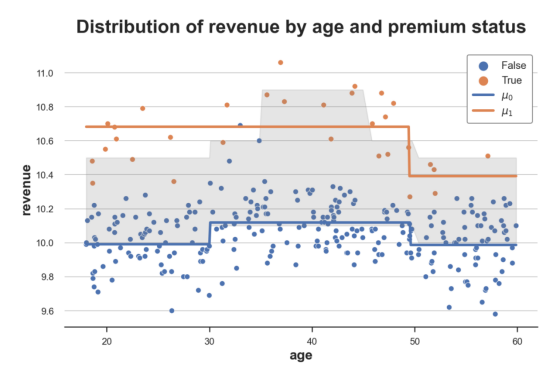
估计效果与真实实验效果比较
上图给出了此部分代码的结果数据以及响应函数μ̂(x,1)和μ̂(x,0)图示。另外,我还使用灰色绘制了真实响应函数之间的区域:真实实验效果。
正如我们从图中看到的,S-learner足够灵活,能够理解实验组和对照组之间的水平差异(我们有两条独立的线)。此外,它还能够很好地捕捉到对照组的响应函数μ̂(x,1),但没有很好地捕捉到实验组的控制函数μ̂(x,1)。
S-learner的问题是,它学习的是单个模型,因此我们必须希望该模型能够揭示实验D中的异质性,但情况可能并非如此。此外,如果由于X的高维数,模型被严重正则化,则可能无法恢复任何实验效果。例如,对于决策树,我们可能不会在实验变量D上进行拆分。
T-learner方案
为了构建双学习器(two-learner)或T-learner的估计量,我们拟合了两个不同的模型,一个用于实验单元,另一个用于对照单元。
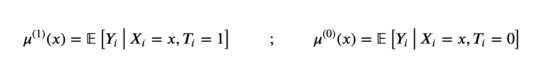
T-learner响应函数
其中,估计量由两个模型的预测值之差得出。
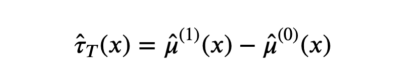
T-learner估计量
def T_learner(df, model, y, D, X):
temp = dgp.generate_data(true_te=True).sort_values(X)
mu0 = model.fit(temp.loc[temp[D]==0, X], temp.loc[temp[D]==0, y])
temp['mu0_hat'] = mu0.predict(temp[X])
mu1 = model.fit(temp.loc[temp[D]==1, X], temp.loc[temp[D]==1, y])
temp['mu1_hat'] = mu1.predict(temp[X])
plot_TE(temp, true_te=True)
我们像以前一样使用决策树回归模型。但是这次,我们为实验组和对照组拟合了两个独立的决策树。
T_learner(dgp, model, y="revenue", D="premium", X=["age"])
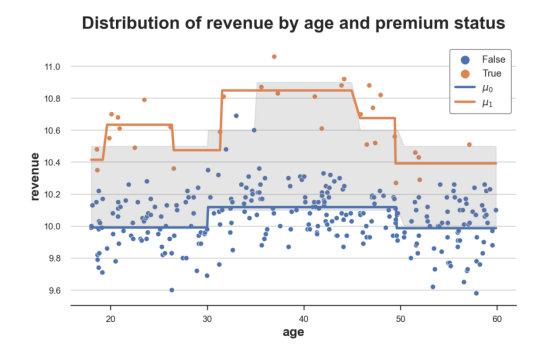
真实与估计的实验效果对比示意图
正如我们所见,T-learner比S-learner灵活得多,因为它适合两种不同的模型。而且,对照组的响应函数μ̂⁽⁰⁾(x)仍然非常准确;同时,实验组的响应函数μ̂⁽¹⁾(x)也比以前更加灵活。
现在的问题是,对于每个预测问题,我们只使用了一小部分数据,而S-learner使用了所有数据。通过拟合两个独立的模型,我们正在丢失一些信息。此外,通过使用两种不同的模型,我们可能会在没有异质性的地方获得异质性。例如,使用决策树,即使数据生成过程相同,我们也可能使用不同的样本获得不同的分割。
X-learner方案
交叉学习器或X学习器(X-learner)估计量是T-learner估计量的扩展。其构建方式如下:
1.对于T-learner,分别使用实验单元与对照单元来单独计算μ̂⁽¹⁾(x)和μ̂⁽0)(x)的模型。
2、计算增量δ函数,如下所示:
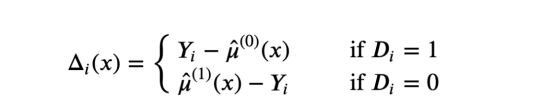
增量δ函数计算方法
3、从X预测Δ,并通过实验单元与对照单元计算τ̂⁽¹⁾(x)。
4、估计倾向得分,即实验概率
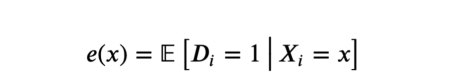
倾向得分
5. 计算实验效果。
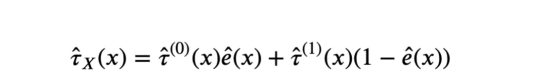
X-learner估计值
为了更好地理解X-learner是如何工作的,我们可以像以前一样来直观地绘制出响应函数。然而,该方法并不直接依赖于响应函数。那么,我们还能恢复伪响应函数吗?是可以的。
首先,我们可以将实验效果改写为:
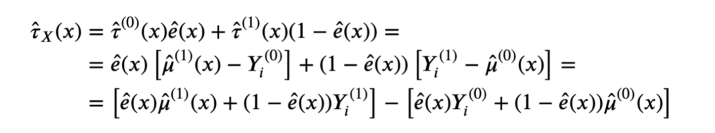
X-learner估计分解展开式
因此,X-learner估计的伪响应函数就可以写成如下形式:
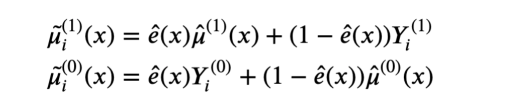
X-learner伪响应函数
正如我们所见,X-learner结合了真实值Yᵢ⁽ᵈ⁾和估计值μ̂ᵢ⁽ᵈ⁾(x),并按倾向分数ê(x)加权(即估计的实验概率)。
这是什么意思呢?这意味着,如果对于某些观察值,我们可以清楚地将实验组和对照组分开,那么对照响应函数μ̂ᵢ⁽ᵈ⁾将获得大部分权重。相反,如果两组无法区分,则实际结果Yᵢ⁽ᵈ⁾将获得大部分权重。
为了说明该方法,我将通过经最近观测得到的近似Yᵢ⁽ᵈ⁾并使用Kneighbors回归函数来构建伪响应函数。我将使用Logistic回归中的LogisticRegressionCV函数来估计倾向分数。
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import LogisticRegressionCV
def X_learner(df, model, y, D, X):
temp = dgp.generate_data(true_te=True).sort_values(X)
# Mu
mu0 = model.fit(temp.loc[temp[D]==0, X], temp.loc[temp[D]==0, y])
temp['mu0_hat_'] = mu0.predict(temp[X])
mu1 = model.fit(temp.loc[temp[D]==1, X], temp.loc[temp[D]==1, y])
temp['mu1_hat_'] = mu1.predict(temp[X])
# Y
y0 = KNeighborsRegressor(n_neighbors=1).fit(temp.loc[temp[D]==0, X], temp.loc[temp[D]==0, y])
temp['y0_hat'] = y0.predict(temp[X])
y1 = KNeighborsRegressor(n_neighbors=1).fit(temp.loc[temp[D]==1, X], temp.loc[temp[D]==1, y])
temp['y1_hat'] = y1.predict(temp[X])
#计算权重
e = LogisticRegressionCV().fit(y=temp[D], X=temp[X]).predict_proba(temp[X])[:,1]
temp['mu0_hat'] = e * temp['y0_hat'] + (1-e) * temp['mu0_hat_']
temp['mu1_hat'] = (1-e) * temp['y1_hat'] + e * temp['mu1_hat_']
#绘图
plot_TE(temp, true_te=True)
X_learner(df, model, y="revenue", D="premium", X=["age"])

真实和估计实验结果示意图
从这张图中我们可以清楚地看到,X-learner的主要优势在于它能够根据上下文调整响应函数的灵活性。在状态空间中有大量数据的区域(对照组),它主要使用估计的响应函数。另外,在状态空间中还有一个显示有少量数据的区域(实验组),这是使用观测值本身的结果。
总结
在本文中,我们学习了Künzel、Sekhon、Bickel、Yu在2019论文中引入的不同估计量,它们利用灵活的机器学习算法来估计异质实验效果。这三个估计量的复杂程度不同。其中,S-learner适合单个估计量,包括作为协变量的实验指标。T-learner适合实验组和对照组的两个独立估计量。最后,X-learner是T-learner的扩展,根据实验组和对照组的可用数据量,能够实现不同程度的灵活性。
异质处理效果的估计对于治疗靶向至关重要,这在企业应用中尤其关键。事实上,这篇文献的引用量迅速增加,并受到广泛关注。在众多其他论文中,值得一提的是Nie和Wager(2021)的R-learner程序以及Athey和Wager(2018)的因果树和森林。我以后可能会撰写更多关于这些程序的内容;所以,请继续关注我的博客。️
参考文献
[1] S. Künzel, J. Sekhon, P. Bickel, B. Yu, Metalearners for estimating heterogeneous treatment effects using machine learning (2019), PNAS.
[2] X. Nie, S. Wager, Quasi-oracle estimation of heterogeneous treatment effects (2021), Biometrika.
[3] S. Athey, S. Wager, Estimation and Inference of Heterogeneous Treatment Effects using Random Forests (2018), Journal of the American Statistical Association.
译者介绍
朱先忠,51CTO社区编辑,51CTO专家博客、讲师,潍坊一所高校计算机教师,自由编程界老兵一枚。早期专注各种微软技术(编著成ASP.NET AJX、Cocos 2d-X相关三本技术图书),近十多年投身于开源世界(熟悉流行全栈Web开发技术),了解基于OneNet/AliOS+Arduino/ESP32/树莓派等物联网开发技术与Scala+Hadoop+Spark+Flink等大数据开发技术。
原文标题:Understanding Meta Learners,作者:Matteo Courthoud


































