人工智能发展七十年,虽然技术指标上不断刷新,但到底什么是「智能」,它如何出现及发展的,还没有答案。
最近马毅教授联手计算机科学家沈向洋博士、神经科学家曹颖教授发表了一篇对智能出现及发展的研究综述,希望将智能体的研究在理论上统一起来,增进对人工智能模型的理解与可解释性。

论文链接:http://arxiv.org/abs/2207.04630
文中引入了两个基本原则:简约(Parsimony)与自洽( Self-consistency)。
作者认为这是智力、人工或自然的兴起的基石。尽管在经典文献里,对这两个原则各自的相关论述、阐述众多,但本文对这两个原则以完全可度量和可计算的方式重新进行解读。
基于这两个第一性的原则,作者推演出了一个高效的计算框架:压缩闭环转录,该框架统一并解释了现代深度网络和许多人工智能实践的演变。
两大基本原则:简约与自洽
在深度学习加持下,过去十年人工智能取得的进展主要依赖于训练同质化的黑箱模型,使用粗暴的工程方法训练大规模神经网络。
虽然性能提高了,也无需手动设计特征,但神经网络内部学到的特征表示却是不可解释的,并且大模型带来其他的难题,比如不断提高的数据收集和计算的成本、学到的表征缺乏丰富性、稳定性(模式崩溃)、适应性(容易出现灾难性遗忘);对变形或对抗性攻击缺乏稳健性等。
作者认为,目前在深度网络和人工智能的实践中出现这些问题的根本原因之一是对智能系统的功能和组织原则缺乏系统和综合的理解。
举个例子,训练用于分类的判别式模型和用于采样或重放的生成性模型基本上在实践中是分开的。这样训练的模型通常叫开环系统,需要通过监督或自监督进行端到端的训练。
在控制理论中,这种开环系统(open-loop systems)不能自动纠正预测中的错误,而且对环境的变化没有适应性;正是因为这样的问题,在控制系统(controlled systems)中大家广泛采用「闭环反馈」,使系统能够自主纠正错误。
类似的经验在学习中也适用:一旦判别式模型和生成性模型结合在一起,形成一个完整的闭环系统,学习就可以变得自主(无需外部监督),而且更有效率、更稳定、更有适应性。
为了理解智能系统中可能需要的功能组件,如判别器或生成器等部件,我们需要从一个更加「原则」和「统一」的角度来理解智能。
文中提出两个基本原则:简约(Parsimony)和自洽(Self-consistency),分别回答了关于学习的两个基本问题。
- 学什么:要从数据中学习什么,如何衡量学到的好坏?
- 怎么学:我们如何通过高效和有效的计算框架来实现这样一个学习的目标?
对于第一个「学什么」的问题,简约原则认为:
智能系统的学习目标就是从外部世界的观测数据中找出低维的结构,并且以最紧凑和结构化的方式重新组织和表示它们。
这也就是「奥卡姆剃刀」原则:如无必要,勿增实体。
如果没有这一原则,智能就不可能发生与存在!如果对外部世界的观测数据没有低维结构,就没有什么值得学习或记忆的东西,也就无法进行良好的泛化或预测。
而且智能系统需要尽量节省资源,如能量、空间、时间和物质等,在某些情况下,该原则也被称为「压缩原则」。但是,智能的简约性(Parsimony of Intelligence)并不是要实现最好的压缩,而是要通过高效的计算手段获得观测数据最紧凑和结构化的表达。
那么简约性该如何度量?
对于一般的高维模型来说,许多常用的数学或统计学「度量」的计算成本都是指数级的,或者对于有低维结构的数据分布来说,甚至是没有定义的,比如最大似然、KL分歧、互信息、Jensen-Shannon和Wasserstein距离等。
作者认为学习的目的实际上就是建立一个映射(通常是非线性的),从原始高维输入中得到一个低维的表示。
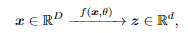
这样,得到的特征z的分布应该更加紧凑和结构化;紧凑意味着存储上更经济;结构化意味着访问和使用更加高效:特别是线性结构,是内插或外推的理想选择。
为了这个目的,作者引入了线性判别表示(LDR),实现三个子目标:
- 压缩:将高维感官数据x映射到低维表征z;
- 线性化:将分布在非线性子面的每一类物体映射到线性子空间;
- 稀疏化:将不同类别映射到相互独立或最不相关的子空间。
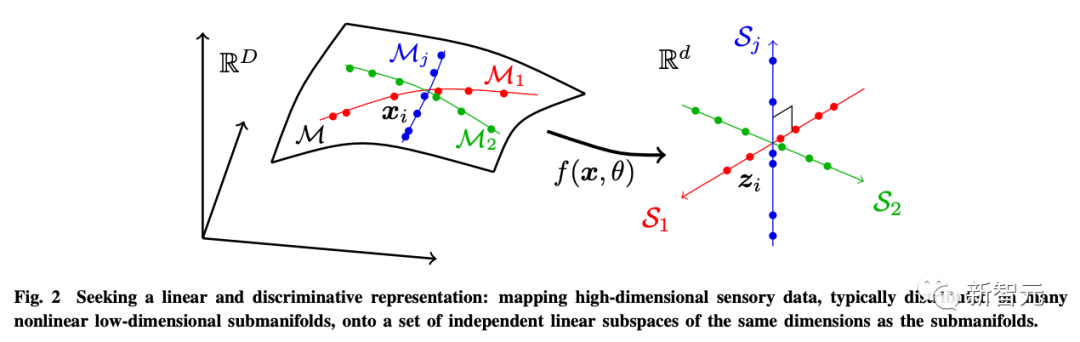
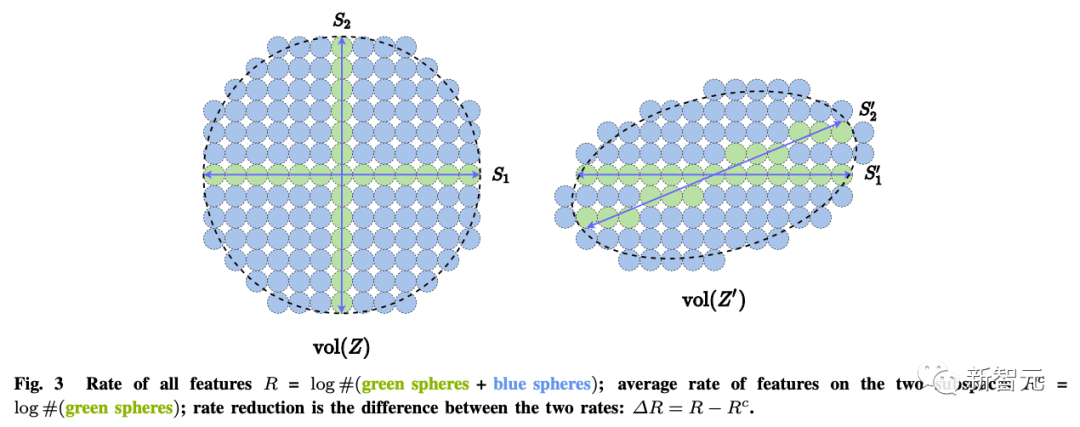
而这几个目标可以通过最大编码率减少(rate reduction)来实现,保证所学到的LDR模型具有最优的简约性能。
对于第二个「怎么学」的问题,自洽原则认为:
一个自主的智能系统通过最小化观测到的数据和再生成的数据在内部表达中的差异,为外部世界的观测寻求一个最自洽的模型。
仅仅是简约原则并不能确保学到的模型能够捕捉到关于外部世界的数据中的所有重要信息。例如,通过最小化交叉熵,将每个类别映射到一个一维的one-hot向量,可以被看作是简约性的一种形式。
它可能会学到一个好的分类器,但学到的特征也可能会崩溃成一个singleton,也称为神经崩溃。这样学到的特征将不再包含足够的信息来重新生成原始数据。
即使我们考虑更普遍的LDR模型,仅靠最大化编码率差也不能自动确定环境特征空间的正确维度。
如果特征空间的维度太低,学到的模型就会与数据不匹配;如果太高,模型可能会过度匹配。
更一般地说,我们认为感知的学习不同于学习具体任务。感知的目标是学习关于所感知的一切可预测的内容。
就像爱因斯坦所说过的:「事情应该力求简单,不过不能过于简单。」
通用学习引擎
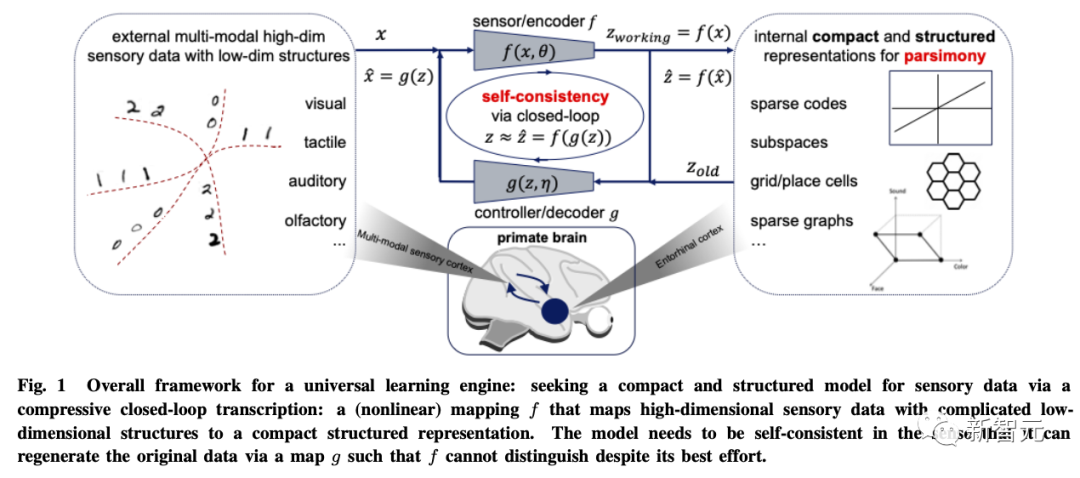
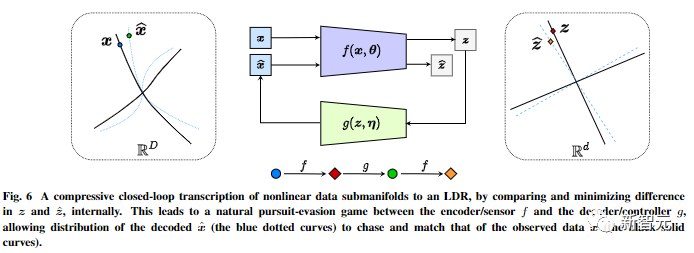
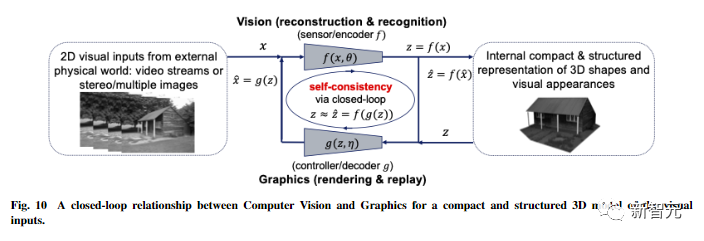
基于这两个原则,文章以视觉图像数据建模为例推导出了压缩闭环转录框架(compressive closed-loop transcription framework)。
其通过比较和最小化内部表征的差异,在内部对非线性数据子流型进行压缩式闭环转录,以实现LDR。
编码器/传感器和解码器/控制器之间的追逃游戏,可以让解码表征生成的数据的分布追逐和匹配观察到的真实数据分布。
另外作者指出,压缩式闭环转录可以有效地进行增量学习。
一个新的数据类的LDR模型可以通过编码器和解码器之间的一个有约束的博弈来学习的:过去学习到的类的记忆可以很自然地作为博弈中的约束被保留,也就是作为闭环转录的「固定点」。
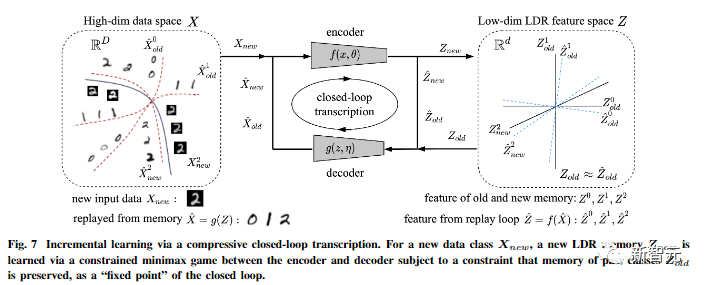
文中还对这个框架的普适性提出了更多的推测性想法,将其扩展到三维视觉和强化学习,并预测其对神经科学、数学和高级智能的影响。
通过这个由第一性原理推导出来的框架:信息编码理论、闭环反馈控制、优化/深度网络和博弈论的概念都有机地整合在一起,成为一个完整的、自主的智能系统的必要组成部分。

值得一提的是,压缩闭环式架构在自然界的所有智能生物以及不同尺度上无处不在:从大脑(压缩感知信息),到脊柱回路(压缩肌肉运动),直至DNA(压缩蛋白质的功能信息)等等。
所以作者认为,压缩性闭环转录应该是所有智能行为背后的「通用学习引擎」。它使得自然的或者人工的智能系统能够从看似复杂的感知数据中发现并提炼出低维的结构,把它们转换为简洁规则的内部表达,以利于将来正确地判断和预测外部世界。
这是一切智能发生和发展的计算基础和机理。
参考资料:http://arxiv.org/abs/2207.04630