译者 | 朱先忠
审校 | 孙淑娟
1.简介
贝叶斯定理为我们提供了一种根据新证据更新信念的方法——当然,还要考虑到我们先前信念的强度。运用贝叶斯定理,你可以试图回答这样一个问题:根据新的证据,我的假设的可能性是多少?
在本文中,我们将讨论贝叶斯定理可以改善数据科学实践的三种方法:
- 更新
- 沟通
- 分类
到文章最后,我相信您将对贝叶斯定理有关的基本概念有一个深刻的理解。
2.方法1:更新
贝叶斯定理为检验假设提供了一种结构,同时考虑了先验假设和新证据的强度,这个过程称为贝叶斯更新。
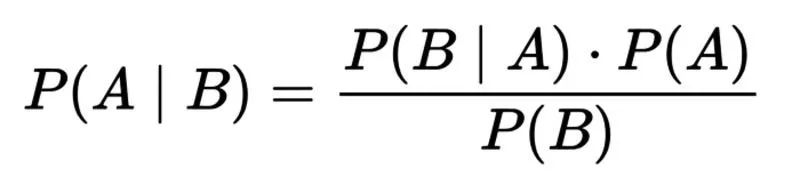
贝叶斯定理:其中A代表假设,B代表与假设相关的新证据
换句话说,这个公式是“在给定B的情况下,A发生的概率等于给定A的情况下B发生的概率乘以A发生的概率除以B发生的概率。”
让我们再深入分析一下这个公式(注意其中含有随机变量的定义内容):
“根据新证据作出假设的概率等于新证据成立的概率(假定假设成立)乘以观察到新证据之前假设成立的概率,除以新证据成立的概率。”
这种表述可以进一步缩短为:
“后验概率等于似然(likelihood)乘以先验概率除以边际似然(marginal likelihood)。”
不管贝叶斯定理现在听起来是否直观,我保证你会一直使用它的。
真实世界示例
比方说,你的朋友打电话来告诉你,她很抱歉,她今晚不能来吃饭。她最近收养了一只宠物考拉,它患上了感冒流鼻涕。她真的需要呆在家里监视考拉的症状情况。
你的假设是,你的朋友不会无缘无故地抛弃你。那么,考虑到她新宠物的最新症状,你的假设成立的似然(likelihood)有多大?

为了评估我们的朋友因为照顾考拉而不在家吃饭的后验概率,我们需要考虑你的朋友需要和考拉呆在家里的概率,因为假设你的朋友是一个正直的人,不会无故放弃晚餐计划。你可能会得出这样的结论:一个通常负责的好朋友很可能会呆在家里照顾宠物。
接下来,我们将似然(likelihood)乘以先验概率。在你的朋友打电话之前,你对她的晚餐计划有多大的信心?如果你认为你的朋友坚如磐石,通常不愿意在最后一刻改变计划,那么你的先验概率很大,无论有什么新的证据,你都不太可能改变这种观点。另一方面,如果你的朋友很脆弱,而你已经想知道她是否会打电话取消,那么你的先验概率很小,这也可能会让她关于和考拉待在家里的说法受到质疑。
最后,我们将上述计算结果除以你的朋友和考拉呆在家里的边际似然。
贝叶斯推理是建立在这种灵活的、常识性的方法基础上的,这种方法根据我们先验知识的强度和新证据的概率来更新我们关于世界的模型。事实上,贝叶斯定理的最初应用是评估上帝的存在。
当涉及到生命和数据科学的关键问题时,你不能抨击贝叶斯定理是一种直观的评估信念如何随时间变化的方法。
3.方法2:沟通
正如贝叶斯定理可以帮助你理解和阐明面对新证据如何更新理论一样,贝叶斯也可以让你成为更强大的数据科学传播者。
数据科学从根本上讲是关于应用数据改进决策的一门科学。
“只有两件事决定你的生活结果:运气和你的决策质量。你只能控制这两件事中的一件。”
——安妮·杜克,扑克游戏冠军兼作家
提高决策质量通常意味着说服决策者。正如每个人的情况一样,您的组织中的决策者正在参与对话。
真实世界示例
我曾经是一家热气球制造商的顾问。我的任务是帮助建立一个数据库,以提高客户对其供应链、制造流程和销售的端到端的理解。
第一天,工厂经理带我们参观了工厂,他自豪地描述了一份新的供应商合同,该合同涉及更轻质、更便宜的原材料。
但有一个问题。当我的团队联系来自整个企业不同数据源的数据表时,我们发现来自新供应商的材料与废料增加2.5%之间存在一定联系。

工厂经理有一个非常强烈的预感,那就是新供应商对他的业务来说很受益。但是,我们却提供了一些相反的证据——我们使用了贝叶斯定理,因为我们理解这样一个事实,即:先验知识越强,需要改变它的证据就越多。
在向工厂经理提出我们的调查结果之前,我们需要收集一些额外的证据来证明不存在导致不同废料水平的其他因素(如磨损的机器、新员工、环境条件等)。
最后,我们向经理提供了更多证据,并帮助他重新谈判供应商合同。
4.方法3:分类
贝叶斯定理可以应用于文本分析的场景,这是一种称为朴素贝叶斯的技术,因为它朴素地假设数据集中每个输入变量(在本例中为每个单词)是独立的。
真实世界示例
假设你发现了一堆你祖父母写的信。他们之间有着一段“动荡不安”的关系,并且有足够的戏剧性浪漫故事——并不局限于真人秀节目中的年轻人间发生的那种。

您需要构建一个情感分类器来确定大部分内容是正面的还是负面的。这其中的一种方法是利用朴素贝叶斯定理。
像朴素贝叶斯这样的生成式分类器将构建一个类别(在本例中为正面的或者是负面的)模型;然后,根据此类别生成一些输入数据。给出一个观察结果(来自字母测试语料库的一个新句子),它返回最有可能产生观察结果的类别。这与学习输入特征预测能力的判别式模型分类器(如逻辑回归)形成对比。
朴素贝叶斯(Naive Bayes)是建立在单词袋技术基础上的。其基本思想是,将文档转换为直方图,以便统计每个单词的使用次数。
您可以使用我们在第#1部分中研究过的稍微修改过的贝叶斯推断公式来计算每个观测值的最可能类别。其实,上面简单修改的是朴素贝叶斯的朴素部分:即假设每个单词的概率在给定的类别中是独立的,于是我们可以将它们相乘,以生成句子随类别一起“落下”的概率。
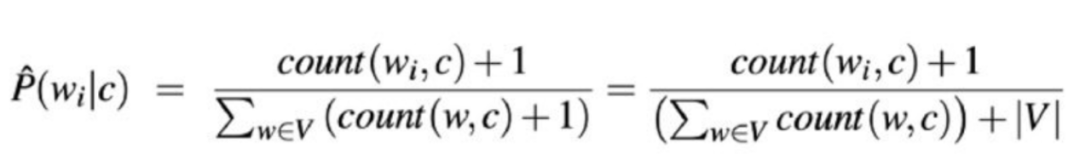
语音和语言处理公式(作者:Daniel Jurafsky和James H.Martin)
在上述公式中,wi表示文档c中单词的计数。公式的分母是单词属于给定类别的条件概率之和。
公式中的+1防止了在类别中没有观察到单词的情况下乘以零的可能性。这种添加一个的技术称为拉普拉斯平滑。
最后,|V|由所有类别中所有单词的并集组成。
贝叶斯定理相关词汇
- 后验概率:根据新证据提出假设的可能性。
- 似然(likelihood):假定假设为真,证据为真的可能性。
- 先验概率:在新证据出现之前,相信假设是真实的。
- 边际似然:证据。
- 朴素贝叶斯:一种分类器算法,它假设数据集的特征之间具有朴素的独立性。
- 生成式分类器:建模特定类,以便确定如何生成输入数据;即是已知类别确定样本。
- 单词袋:将文档转换为直方图的简化文本表示。
- 拉普拉斯平滑:一种简单的加法平滑技术,可避免乘以零。
5.小结
我有一个强烈的先验信念,即贝叶斯定理对数据科学家十分有用;但是,我还是会根据您在评论中给我的反馈来更新后验概率。总之,我期待着您的来信,告诉我您是如何在生活和工作中使用贝叶斯定理的。
原文链接:https://www.kdnuggets.com/2022/06/3-ways-understanding-bayes-theorem-improve-data-science.html
译者介绍
朱先忠,51CTO社区编辑,51CTO专家博客、讲师,潍坊一所高校计算机教师,自由编程界老兵一枚。早期专注各种微软技术(编著成ASP.NET AJX、Cocos 2d-X相关三本技术图书),近十多年投身于开源世界(熟悉流行全栈Web开发技术),了解基于OneNet/AliOS+Arduino/ESP32/树莓派等物联网开发技术与Scala+Hadoop+Spark+Flink等大数据开发技术。





























