作者 | vivo 互联网数据分析团队-Dong Chenwei,vivo 互联网大数据团队-Qin Cancan、Zeng Kun
本文介绍了vivo游戏中心在灰度数据分析体系上的实践经验,从“实验思想-数学方法-数据模型-产品方案”四个层面提供了一套较为完整的智能灰度数据解决方案,以保障版本评估的科学性、项目进度以及灰度验证环节的快速闭环。该方案的亮点在于,指标异动根因分析方法的引入和全流程自动化产品方案的设计。
一、引言
游戏业务的用户规模体量大,业务链路长,数据逻辑繁杂。游戏中心作为游戏业务平台端的核心用户产品,版本迭代非常频繁,每次版本上线前都必须进行小量级的灰度验证。2021年以来,平均每1~2周都会有重要版本开始灰度,而且线上有时会同时有多个版本在灰度测试。
灰度的整个过程在数据层面主要涉及3个问题:
- 如何确保版本灰度评估的科学性?
- 如何提升灰度数据的产出效率,保障项目进度?
- 当灰度版本出现指标异常问题时,如何快速定位问题完成闭环?
近两年来,我们逐步将灰度评估方法体系化地落地到敏捷BI等数据产品上,目前灰度数据体系已经较好地解决了这3个问题。本文首先以版本灰度数据体系的基本概念和发展历程为铺垫,接着以“方法论+解决方案”为主线阐述游戏中心在灰度数据体系上的实践,并展望未来。
二、灰度数据体系的发展
2.1 什么是灰度发版
当游戏中心开发了全新的首页界面,应该如何验证新的首页是否被用户所接受,并且功能是否完善、性能是否稳定?
答:灰度发版。就是在新版本推送给全量用户使用之前,按照一定策略选取部分用户,让他们先行体验新版首页,以获得他们关于“新的首页好用或不好用”以及“如果不好用,是哪里出了问题”的使用反馈。如果出现重大问题,则及时回滚旧版本;反之则根据反馈结果进行查漏补缺,并适时继续放大新版本投放范围直至全量升级。
2.2 灰度评估方案发展阶段
判断灰度发版是否科学的关键在于控制变量,这一问题的解决过程,也是灰度评估方案迭代和发展的过程。
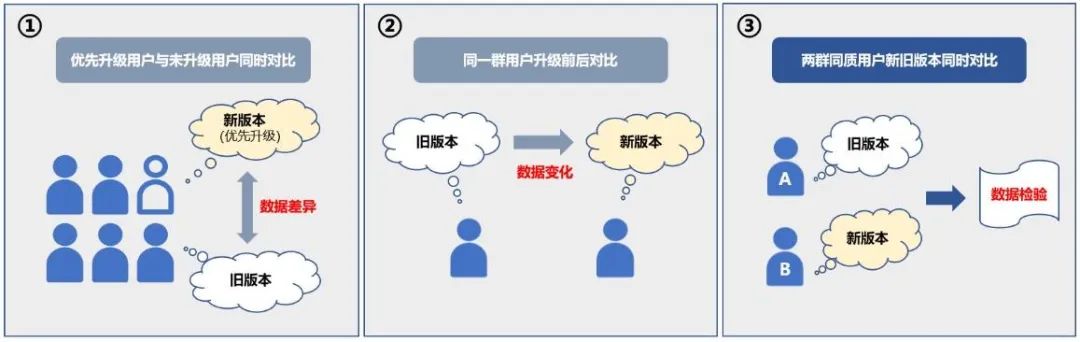
阶段一:确保了对比的时间相同,但升级速度差异意味着优先升级的用户和未升级的用户非同质用户,未能规避样本差异对数据结果差异的影响。
阶段二:确保了对比的人群相同,但用户行为可能随时间而变化,无法剔除前后时间因素的差异。
阶段三:同时确保了时间和人群相同,有以下三方面优势:
- 将旧版本打包为对比包,与新版本的灰度包一起,分别对两批同质用户发布,保证了灰度包和对比包的样本属性、时间因素一致;
- 依据产品目标计算合理的样本量,避免样本过少导致结果不可信、过多导致资源浪费;
- 依托静默安装功能快速升级,缩短灰度验证阶段的时间。
2.3 灰度数据体系内容
灰度数据体系通常涉及前期流量策略和后期数据检验2个部分。
前者包括样本量计算和灰度时长控制,后者包括新老版本核心指标对比、产品优化处的指标变化或新增功能的数据表现。在常规的灰度评估之外,引入根因分析的方法可以提升灰度结果的解释性。
2.4 vivo游戏中心的做法
我们搭建了“游戏中心智能灰度数据体系”,并通过三版迭代逐步解决了本文开头提到的3个问题。数据体系由指标检验结果、维度下钻解读、用户属性校验、指标异常诊断等主题看板以及自动化推送的灰度结论报告组成。
完整方案部署上线后,基本实现了灰度评估阶段的自动化数据生产、效果检验、数据解读和决策建议的闭环,极大地释放了人力。
三、灰度数据体系中的方法论
在介绍数据方案设计前,先介绍一下灰度数据体系中涉及的背景知识和方法论,帮助大家更好地理解本文。
3.1 灰度实验
灰度实验包括抽样和效果检验两个部分,对应的是假设检验的思想以及样本历史差异性验证。
3.1.1 假设检验
假设检验是先对总体参数提出一个假设值,然后利用样本表现判断这一假设是否成立。
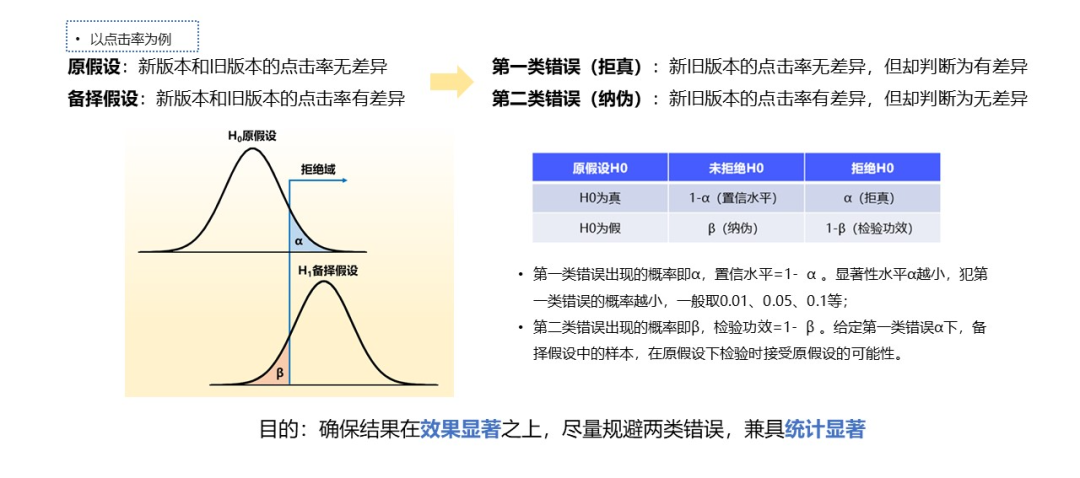
3.1.2 样本历史差异性验证
虽然灰度前事先已通过hash算法进行抽样,但由于抽样的随机性,一般会在统计检验和效果检验的同时,对样本的历史差异性进行验证,剔除样本本身差异带来的指标波动。灰度周期通常为7天,我们采用了7天滑动窗口取样的方法。

3.2 根因分析
灰度指标往往与多维属性(如用户属性、渠道来源、页面模块等)存在关联,当指标的检验结果发生异常的显著差异时,想要解除异常,定位出其根因所在是关键一步。然而,这一步常常是充满挑战的,尤其当根因是多个维度属性值的组合时。
为了解决这一问题,我们引入了根因分析的方法,以弥补了灰度检验结果解释性不足的问题。我们结合了指标逻辑分析法和Adtributor算法2种方法,以确保分析结果的可靠性。
3.2.1 指标逻辑分析法
由于灰度实验中构建的指标体系基本都是率值类指标或均值类指标,这两类指标都可以通过指标公式拆解为分子和分母两个因子,而指标的分子和分母均是由各个维度下的维度值相加得到。因此提出了指标逻辑分析法,基于一定的拆解方法,从指标因子和指标维度2个层次对指标值进行逻辑拆解。

3.2.2 Adtributor算法
除了根因分析比较常见的维度下钻方法以外,我们引入了Adtributor算法,以更好地应对多维度组合影响指标的情况,并通过两种方法的交叉验证来确保分析结果的可靠性。
Adtributor算法是微软研究院于2014年提出的一种多维时间序列异常根因分析方法,在多维度复杂根因的场景下具有良好的可靠性。算法完整过程包括数据预处理、异常检测、根因分析和仿真可视化4个步骤,我们主要借鉴了根因分析环节的方法。

四、灰度智能解决方案
4.1 整体框架
版本灰度可以分为灰度前-灰度中-灰度后3个阶段,产品化整体框架如下:
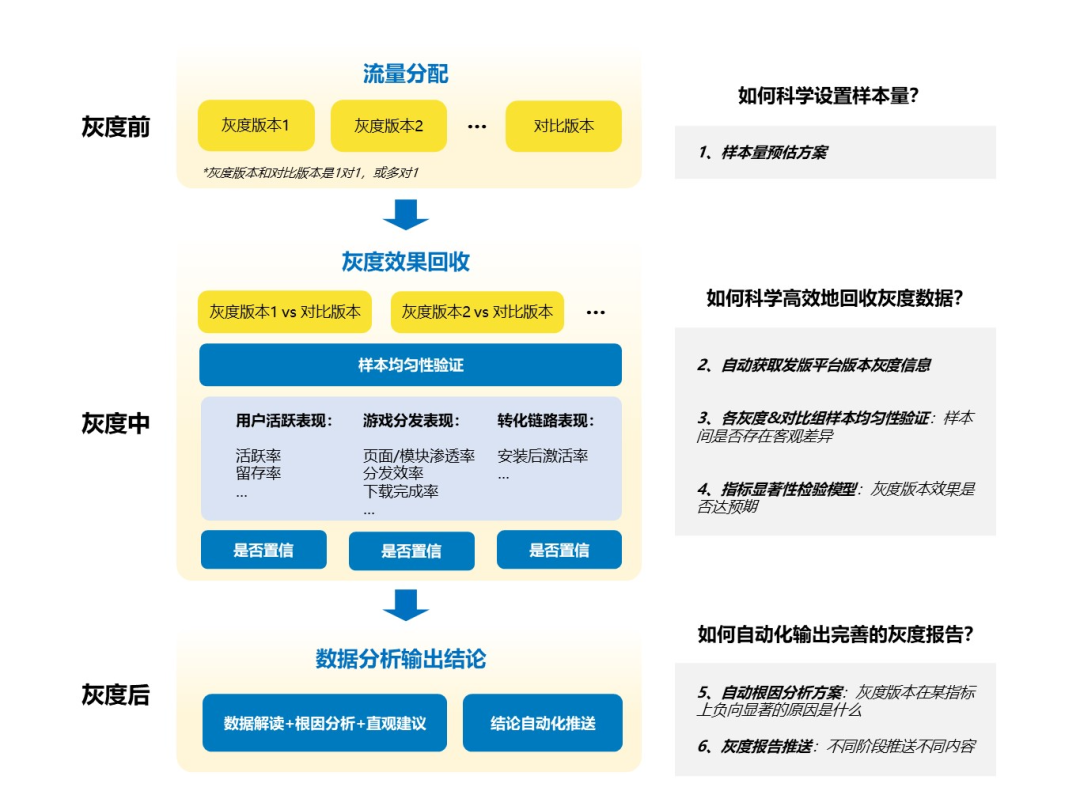
4.2 流程设计
基于以上框架,我们是如何设计实现的?
以下是描述整个过程的流程图:
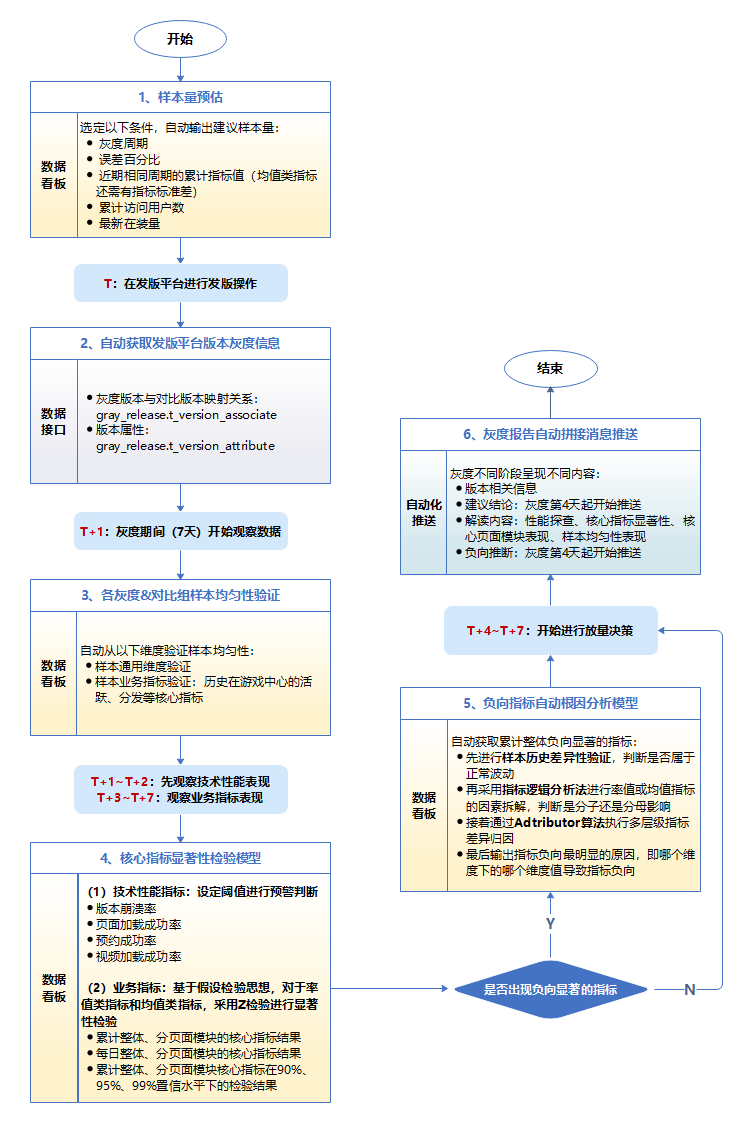
4.3 方案核心内容
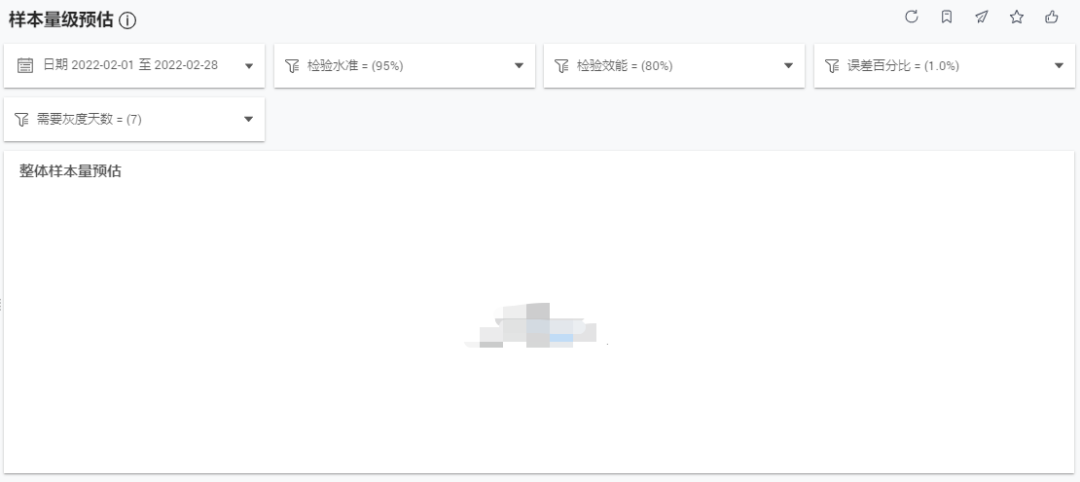
4.3.1 样本量预估方案
看板提供:在多套置信水平跟检验效能标准下(默认显示95%置信度、80%检验效能),根据指标最近表现,预估出指标在不同预期变化幅度下能被检测出显著与否的最低样本量。
该方案具有3大特点:
- 输出多套标准,灵活调整预期幅度;
- 自动选取最近一个全量版本的数据作为数据输入;
- 均值类指标和率值类指标采用差异化的计算逻辑。
4.3.2 效果指标显著性检验方案
指标显著性检验模型需要回答的问题是:灰度版本相较对比版本,指标变化在统计意义上是置信的还是不置信的。
目前,实现了三种置信水平下灰度版本与对比版本在20个业务指标上的显著性判断。
实现过程如下:
率值类指标
... ...
# 已得以下指标数据
variation_visitors # 灰度版本指标分母
control_visitors # 对比版本指标分母
variation_p # 灰度版本指标值
control_p # 对比版本指标值
z # 不同置信水平(90%/95%/99%)下的z值,业务上主要关注95%置信水平下的显著检验结果
# 计算指标标准差
variation_se = math.sqrt(variation_p * (1 - variation_p))
control_se = math.sqrt(control_p * (1 - control_p))
# 计算指标变化值和变化率
gap = variation_p - control_p
rate = variation_p / control_p - 1
# 计算置信区间
gap_interval_sdown = gap - z * math.sqrt(math.pow(control_se, 2) / control_visitors + math.pow(variation_se, 2) / variation_visitors) # 变化值置信区间下界
gap_interval_sup = gap + z * math.sqrt(math.pow(control_se, 2) / control_visitors + math.pow(variation_se, 2) / variation_visitors) # 变化值置信区间上界
confidence_interval_sdown = gap_interval_sdown / control_p # 变化率置信区间下界
confidence_interval_sup = gap_interval_sup / control_p # 变化值置信区间上界
# 显著性判断
if (confidence_interval_sdown > 0 and confidence_interval_sup > 0) or (confidence_interval_sdown < 0 and confidence_interval_sup < 0):
print("显著")
elif (confidence_interval_sdown > 0 and confidence_interval_sup < 0) or (confidence_interval_sdown < 0 and confidence_interval_sup > 0):
print("不显著")
... ...- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
均值类指标
... ...
# 已得以下指标数据
variation_visitors # 灰度版本指标分母
control_visitors # 对比版本指标分母
variation_p # 灰度版本指标值
control_p # 对比版本指标值
variation_x # 灰度版本单用户指标值
control_x # 对比版本单用户指标值
z # 不同置信水平(90%/95%/99%)下的z值,业务上主要关注95%置信水平下的显著检验结果
# 计算指标标准差
variation_se = np.std(variation_x, ddof = 1)
control_se = np.std(control_x, ddof = 1)
# 计算指标变化值和变化率
gap = variation_p - control_p
rate = variation_p / control_p - 1
# 计算置信区间
gap_interval_sdown = gap - z * math.sqrt(math.pow(control_se, 2) / control_visitors + math.pow(variation_se, 2) / variation_visitors) # 变化值置信区间下界
gap_interval_sup = gap + z * math.sqrt(math.pow(control_se, 2) / control_visitors + math.pow(variation_se, 2) / variation_visitors) # 变化值置信区间上界
confidence_interval_sdown = gap_interval_sdown / control_p # 变化率置信区间下界
confidence_interval_sup = gap_interval_sup / control_p # 变化值置信区间上界
# 显著性判断
if (confidence_interval_sdown > 0 and confidence_interval_sup > 0) or (confidence_interval_sdown < 0 and confidence_interval_sup < 0):
print("显著")
elif (confidence_interval_sdown > 0 and confidence_interval_sup < 0) or (confidence_interval_sdown < 0 and confidence_interval_sup > 0):
print("不显著")
... ...- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
看板展示如下:
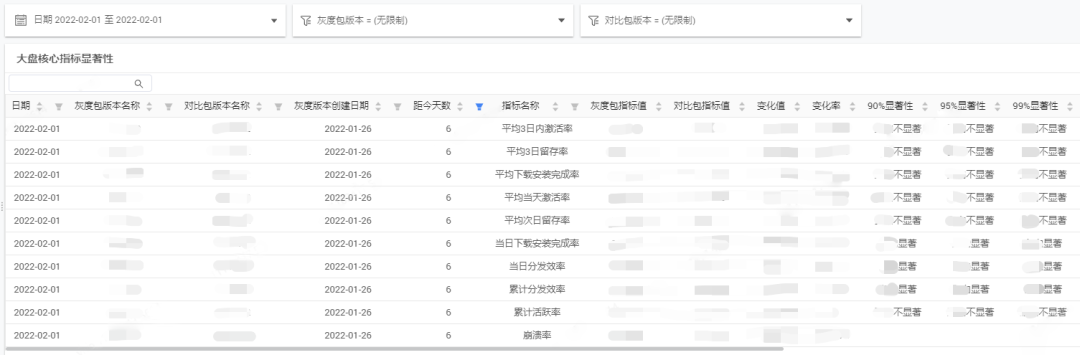
4.3.3 负向指标自动根因分析方案
灰度场景的负向指标自动化根因分析方案包括异动检测、样本历史差异性验证、指标逻辑拆解和Adtributor自动根因分析4个步骤。
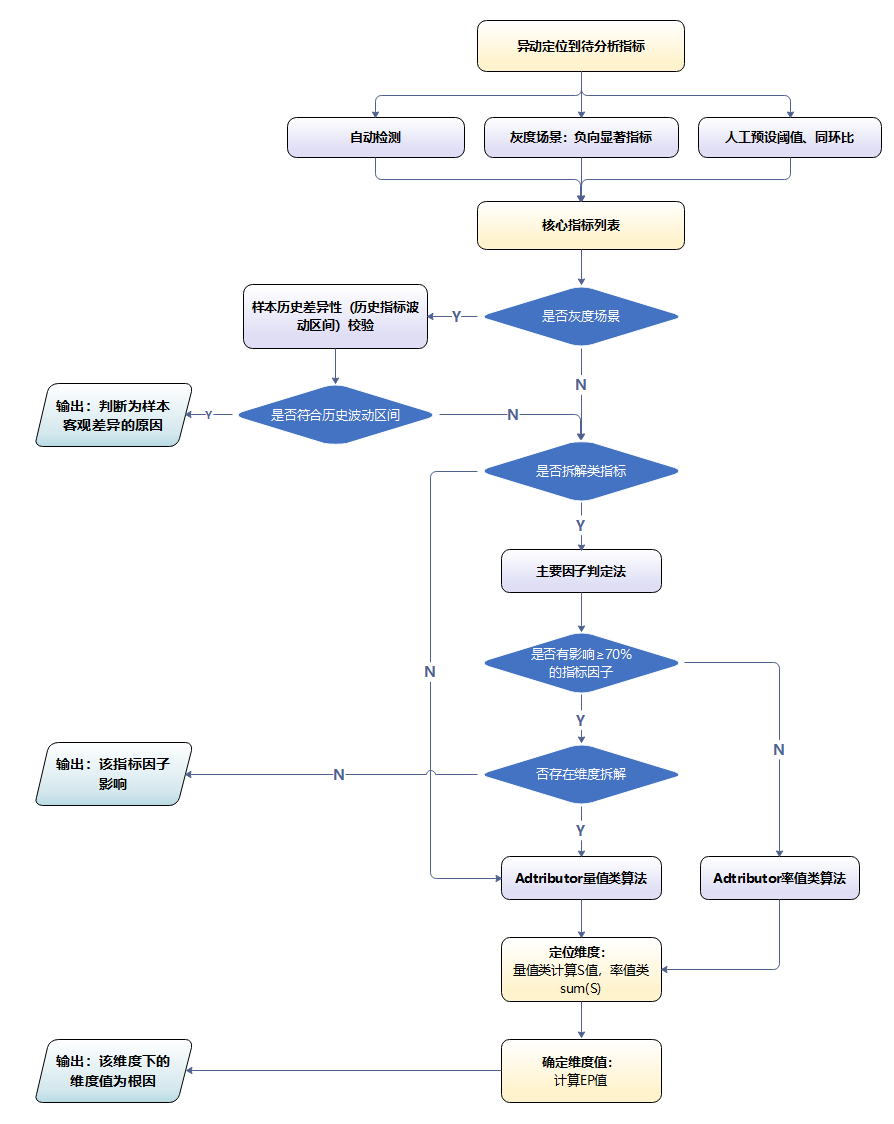
其中,Adtributor自动根因分析能计算出同一层级的维度中对指标异动贡献最大的那个因素,我们通过对指标维度进行分层和设置相互关系来适应具体的指标业务场景,构建起多层级归因算法逻辑模型,从而实现业务层面根因结论的自动化输出。
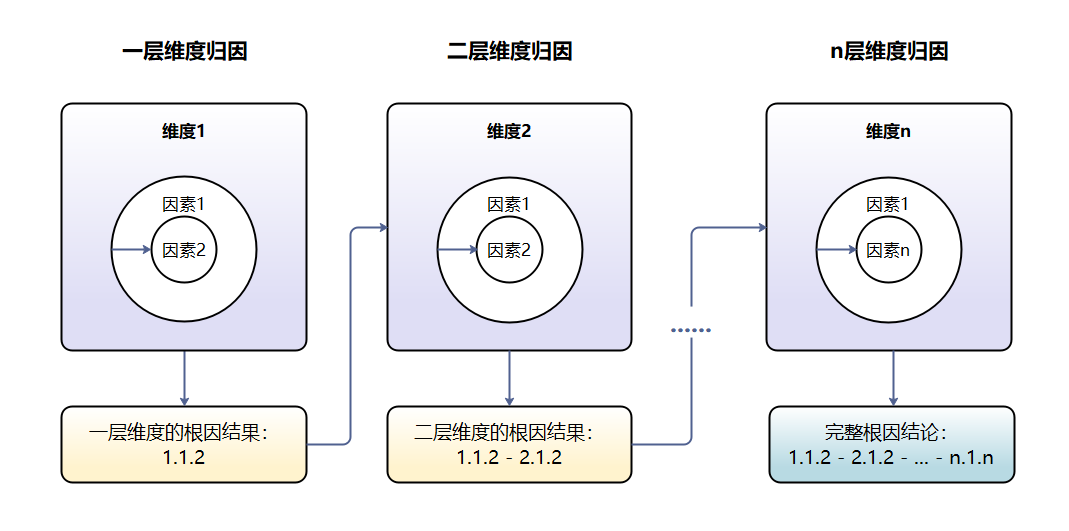
看板展示如下:
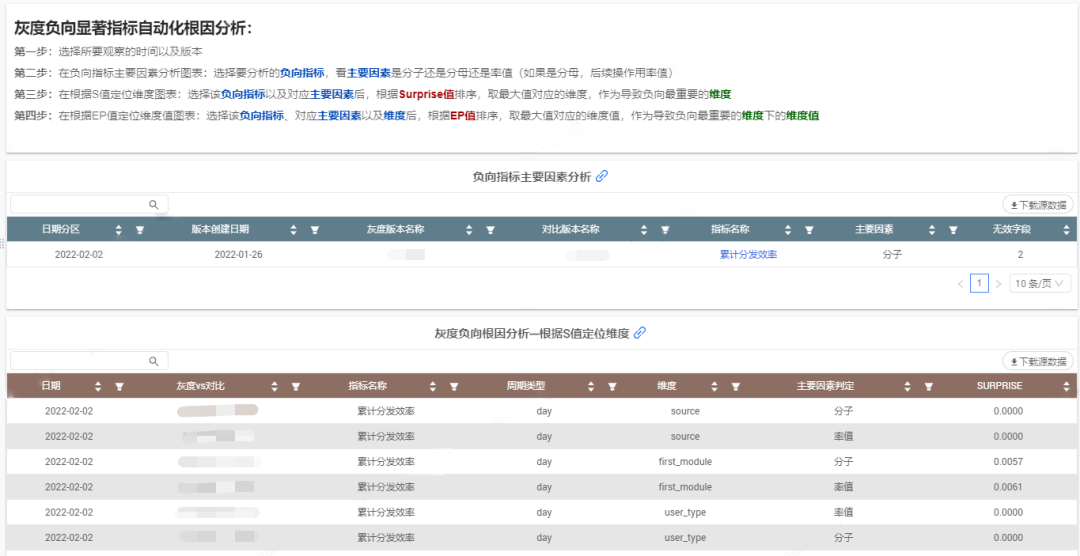
4.3.4 灰度报告智能拼接推送方案

版本信息内容的自动获取:
通过打通发版平台获取版本号、实际在装量、发版累计天数以及版本相关内容,作为灰度报告的开头。
结论呈现:
根据指标是否全正向/部分负向/全负向、是否样本不均匀等各种统计结果自动组合对应到预设的结论文案中,一共预设了10多种结论模版。
核心指标显著性检验解读(根据灰度阶段不同,解读不同类型指标):
T+1~T+2:性能类指标、活跃率指标
- T+3~T+6:活跃表现指标、分发表现指标、下载安装过程转化指标
- T+7:活跃表现指标、分发表现指标、下载安装过程转化指标、后项转化类指标
下钻一级模块维度归因解读:
如果灰度版本前期已明确输入具体到某个一级模块的改动点,会自动进行该模块的解读,以及输出其他有指标差异的模块的数据;如果灰度版本没有输入模块层面的改动点,就输出指标效果显著(正向显著、负向显著)的一级模块的解读结论。
样本量均匀性解读:
业务类指标,通过显著性检验判断是否分布均匀;非业务类指标,通过分布差异来判断。
负向诊断解读:
根据多层级自动化根因模型输出的结果,按照不同维度类型映射的修饰词、维度数量定位(单维度/多维度)以及样本历史差异性验证结论,对应不同的模版,最终拼接出负向诊断文案。
五、写在最后
对于业务灰度发版中科学评估和快速决策的要求,我们结合了多种方法,从“实验思想-数学方法-数据模型-产品方案”四个层面提供了一套较为完整的智能灰度数据体系解决方案。
本文希望能为业务中的灰度数据体系建设提供参考,但仍应结合各业务自身的特点进行合理设计。方案中涉及的数据模型设计在这里不详细介绍,感兴趣的同学欢迎和笔者一起探讨学习。
此外,灰度数据体系仍有待改进之处,这里先抛出来,有一些也已经在研究解决中:
- 在灰度流量分组的时候,通常采用随机分组的方式。但是由于完全随机的不确定性,分完组后,2组样本在某些指标特性上可能天然就分布不均。相较于后置的样本均匀性验证的方法,也可考虑分层抽样的方式来避免这一问题;
- 在灰度指标分析的流程中,自动多维根因分析模型还存在提升的空间,目前模型非常依赖于本身数据源中维度的全面性,且只能检测出定量部分的原因。后续希望把定量的根因模型,结合定性因素进行更全面更准确的解读;
- 游戏中心目前整个灰度的解决方案本质上还是基于2 sample-test的检验模型,但该模型需要根据灰度版本相较于对比版本在核心指标上的预期提升,来提前估算最小样本量,实际灰度过程中可能会出现核心指标未达如预期的情况。未来可尝试mSPRT等检验方法,削弱最小样本量对显著性结果的限制。
参考文献:
- 茆诗松, 王静龙, 濮晓龙. 《高等数理统计(第二版)》
- 是老李没错了. 《五分钟掌握AB实验和样本量计算原理》. CSDN博客
- Ranjita Bhagwan, Rahul Kumar, Ramachandran Ramjee, et al. 《Adtributor: Revenue Debugging in Advertising Systems》