
大家好,我是年年!今天的内容是关于一道算法题——青蛙跳台阶。这是一个面试很喜欢考的题,看到它,大部分人脑海中应该立马出现:斐波那契亚数列——递归——f(n)=f(n-1)+f(n-2)。
但辅导的小伙伴上周在面试中遇到的问题是:除了递归,能不能写出别的解法,降低算法的时间复杂度。这篇文章给出这道题的更优解。
题目
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个n级的台阶总共有多少种跳法?
分析
这是一个最基础的动态规划类问题,首先来讲一下思路:当n较小时,可以直接枚举得到结果:
- n=1时,青蛙仅有直接跳上一级台阶这种跳法,即一种跳法;
- n=2时,青蛙可以先跳 上 1 级,然后再跳 上 1 级到达2级台阶,;也可以直接跳 2 级台阶,即一共有两种解法;
当n较大时,去枚举不现实了。但可以想象一下青蛙“最后一跳”有哪些情况:因为青蛙一次可以跳1个或2个台阶,所以只可能是两种情况:从n-1级跳1级上去,以及从n-2阶的位置跳2级上去。我们想要知道跳n级台阶有多少种解法,只需要知道跳n-1级台阶和跳n-2级台阶的跳法,把他们加起来就可以。即得到一个公式f(n)=f(n-1)+f(n-2)。
常规解法(递归)
看到这个式子f(n)=f(n-1)+f(n-2),应该很快能反应:斐波那契亚数列,代码很容易写出来。递归的关键是确认递归出口,即:当只有1级台阶,只有一种跳法;只有2级台阶时,有两种跳法。
代码如下:
function frogJump(n) {
if (n >= 3) {
let result = frogJump(n - 1) + frogJump(n - 2)
return result
} else if (n === 1) {
return 1
}else if(n===2) {
return 2
}
}
let result = frogJump(6) // 13
console.log(result)
复杂度分析
上面这张递归解法只有60分,因为时间复杂度太高。
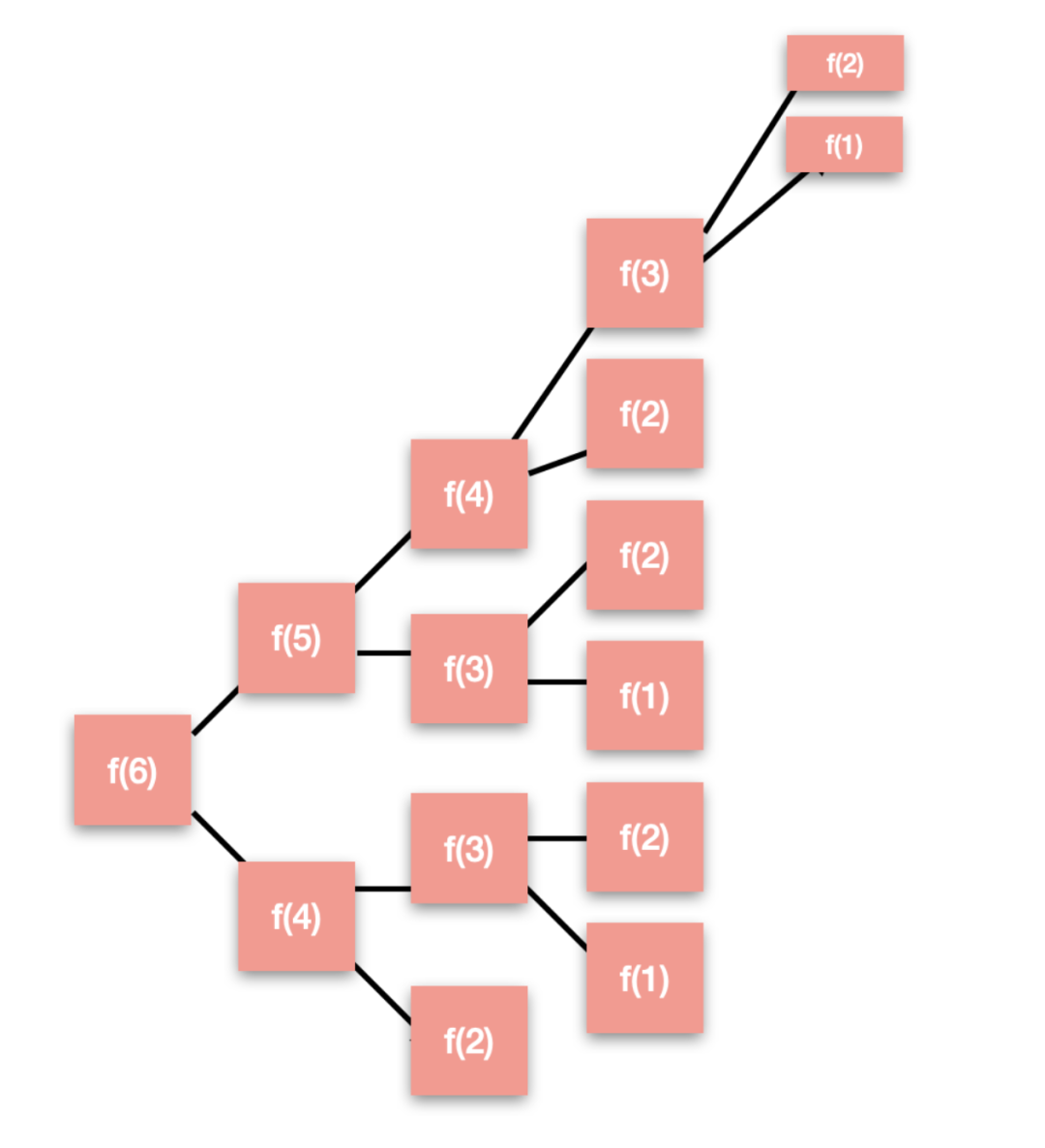
可以看到,因为没有把结果保存,出现了很多重复计算的步骤:为了得到f(6)的结果,需要计算f(5)和f(4),为了得到f(5)的结果,需要计算f(4)和f(3),这里两次计算f(4)是独立的事件,也就是说,我们做了很多重复工作。
把上面这棵树补充成一个完全树,如下:
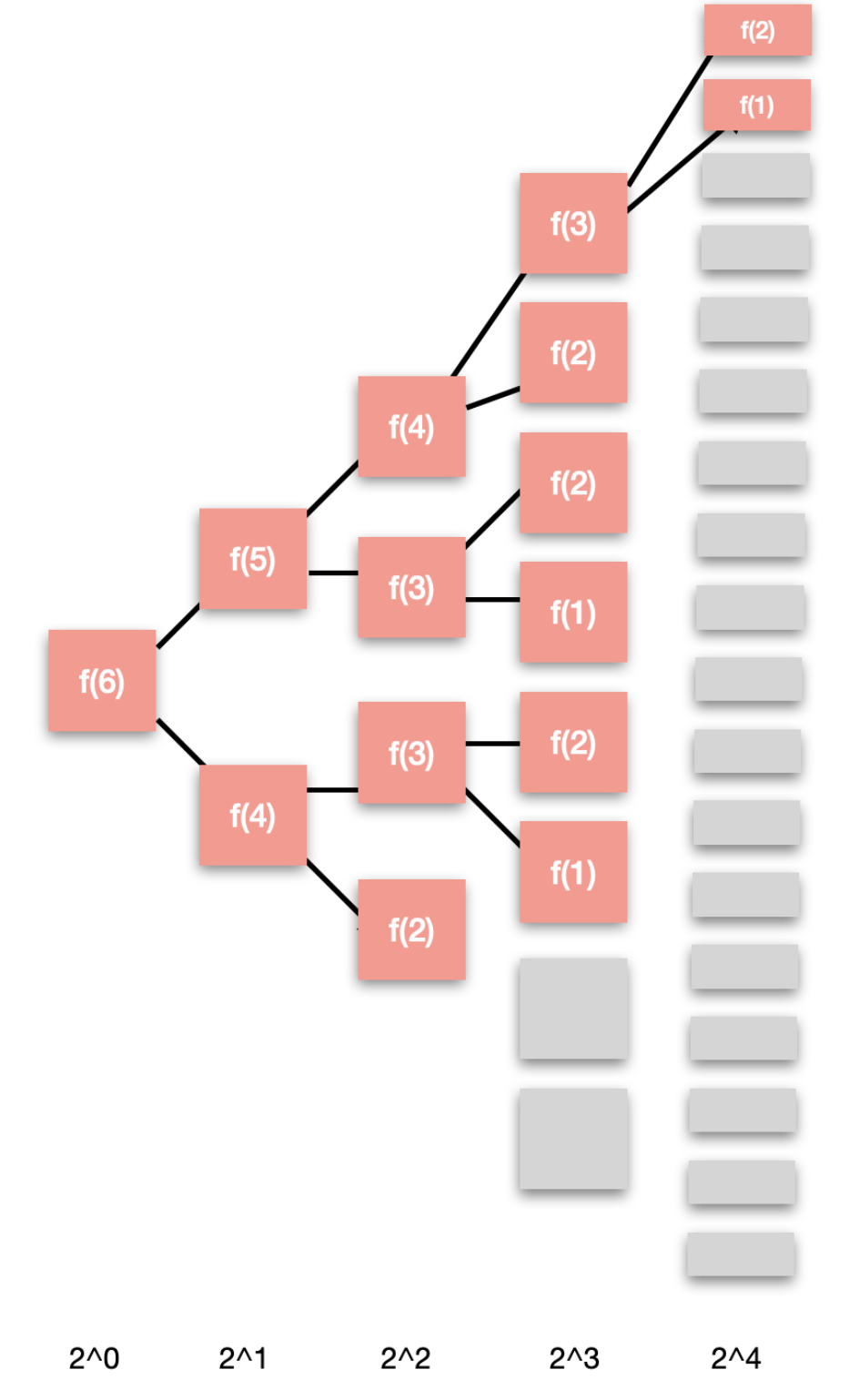
这种算法复杂度可以用2^0+2^1+2^2+...+2^4表示,即时间复杂度近似为O(2^N)(回忆一下高中数学的等比数列)。
而空间复杂度是调用栈的深度,从上面的图可以看出来,最大的栈深是n-1,即空间复杂度是O(n)
进阶解法(尾递归)
上面这种解法时间复杂度很高在于做了很多重复计算,从递归公式能看出来:f(n)=f(n-1)+f(n-2)=f(n-2)+f(n-3)+f(n-3)+f(n-4),一生二,二生四,四生八,整个计算过程就像是发散开来一样。每一次调用都没有保留下“状态”,造成了大量的计算浪费。
只要我们保留下计算的结果,就可以把时间复杂度控制在O(n),也就是下面“尾递归”。
代码如下:
function frogJump(first, second, n) {
let a = first,
b = second
let c = first + second
if (n > 3) {
a = second
b = first + second
return frogJump(a, b, n - 1)
} else if (n === 3) {
return c
} else if ( n === 2) {
return 2
} else if(n===1) {
return 1
}
}
let result = frogJump(1, 2, 6)
console.log(result)
我们用abc三个变量,把计算的结果保存下来,避免重复的工作。从first=1,second=2开始计算,每次递归调用更新first和second的值,这就是在保存下每次计算的结果,供下一次递归使用。直到n=3,满足递归终止条件。
复杂度分析
这种尾递归,时间复杂度只有O(N),但他是几种解法里面最难想到,也最难理解的。空间复杂度即递归的深度,是O(N)。
进阶解法(循环)
循环和递归是可以相互转化的,所以一种优化思路是用循环把上面的逻辑实现。
function frogJump(n) {
if (n === 1) {
return 1
} else if(n===2) {
return 2
}else {
let a = 1,
b = 2,
c
let count = 0
while (count < n - 2) {
c = a + b
a = b
b = c
count++
}
return c
}
}
let result = frogJump(6)
console.log(result)
我们首先知道了计算公式f(n)=f(n-1)+f(n-2);并且知道:当只有一级台阶时,只有一种解法,只有两级台阶时,只有两种解法。如果有三级台阶,计算一次即可(计算F(3));有四级台阶,计算两次即可(计算f(3)、f(4))所以可推,当计算f(n)时,需要计算的次数是n-2,这就是循环的次数。上面的代码便不难写出。
复杂度分析
通过循环,我们同样保留下了计算的结果,减少了重复的工作,时间复杂度是O(N)。空间复杂度是O(1)。
结语
通过这道算法题,能感受到循环通常比递归在时间复杂度上有优势,但它更难想到,代码块也会更复杂。通常一个算法的递归和循环是可以相互转化的,可以试着把之前刷过的题用不同的思路实现一下。































