深度学习研究者从神经科学和认知科学中汲取灵感,从隐藏单元、输入方式,到网络连接、网络架构的设计等,许多突破性研究都基于模仿大脑运行策略。毫无疑问,近年来在人工网络中,模块化和注意力经常被组合使用,并取得了令人印象深刻的结果。
事实上,认知神经科学研究表明,大脑皮层以模块化的方式表示知识,不同模块之间进行通信,注意力机制进行内容选择,这也就是上述提到的模块化和注意力组合使用。在近期的研究中,有人提出,大脑中的这种通信方式可能对深度网络中的归纳偏置有意义。这些高级变量之间依赖关系的稀疏性,将知识分解为尽可能独立的可重组片段,使得学习更有效率。
尽管最近的许多研究都依赖于这样的模块化体系架构,但研究者使用了大量的技巧以及体系架构修改,这使得解析真正的、可用的体系架构原则变得具有挑战性。
机器学习系统正逐渐显露出更稀疏、更模块化架构的优势,模块化架构不仅具有良好的泛化性能,而且还能带来更好的分布外(OoD) 泛化、可扩展性、学习速度和可解释性。此类系统成功的一个关键是,用于真实世界设置的数据生成系统被认为由稀疏交互部分组成,赋予模型类似的归纳偏置将是有帮助的。然而,由于这些真实世界的数据分布是复杂和未知的,该领域一直缺乏对这些系统进行严格的定量评估。
由来自加拿大蒙特利尔大学的 Sarthak Mittal、Yoshua Bengio、 Guillaume Lajoie 三位研究者撰写的论文,他们通过简单且已知的模块化数据分布,对常见的模块化架构进行了全面评估。该研究强调了模块化和稀疏性的好处,并揭示了在优化模块化系统时面临挑战的见解。一作及通讯作者 Sarthak Mittal 为 Bengio 和 Lajoie 的硕士生。

- 论文地址:https://arxiv.org/pdf/2206.02713.pdf
- GitHub 地址:https://github.com/sarthmit/Mod_Arch
具体而言,该研究扩展了 Rosenbaum 等人的分析,并提出了一种方法来评估、量化和分析模块化架构的常见组成部分。为此,该研究开发了一系列基准和指标,旨在探索模块化网络的效能。这揭示了有价值的见解,不仅有助于识别当前方法的成功之处,还有助于识别这些方法何时以及如何失败的。
该研究的贡献可总结为:
- 该研究基于概率选择规则来开发基准任务和指标,并用基准和指标来量化模块化系统中的两个重要现象:崩溃(collapse)和专业化(specialization)。
- 该研究提炼出常用的模块化归纳偏置,并通过一系列模型进行系统地评估,这些模型旨在提取常用的架构属性(Monolithic, Modular, Modular-op、GT-Modular 模型)。
- 该研究发现,当一个任务中有很多潜在规则时,模块化系统中的专业化可以显著提高模型性能,但如果只有很少的规则,则不会如此。
- 该研究发现,标准的模块化系统在专注于正确信息的能力和专业化能力方面往往都不是最优的,这表明需要额外的归纳偏置。
定义 / 术语
本文中,研究者探究了一系列模块化系统如何执行常见的任务,这些任务由我们称为规则数据的合成数据生成过程制定。他们介绍了关键组成部分的定义,包括(1)规则以及这些规则如何形成任务,(2)模块以及这些模块如何采用不同的模型架构,(3)专业化以及如何评估模型。详细设置如下图 1 所示。
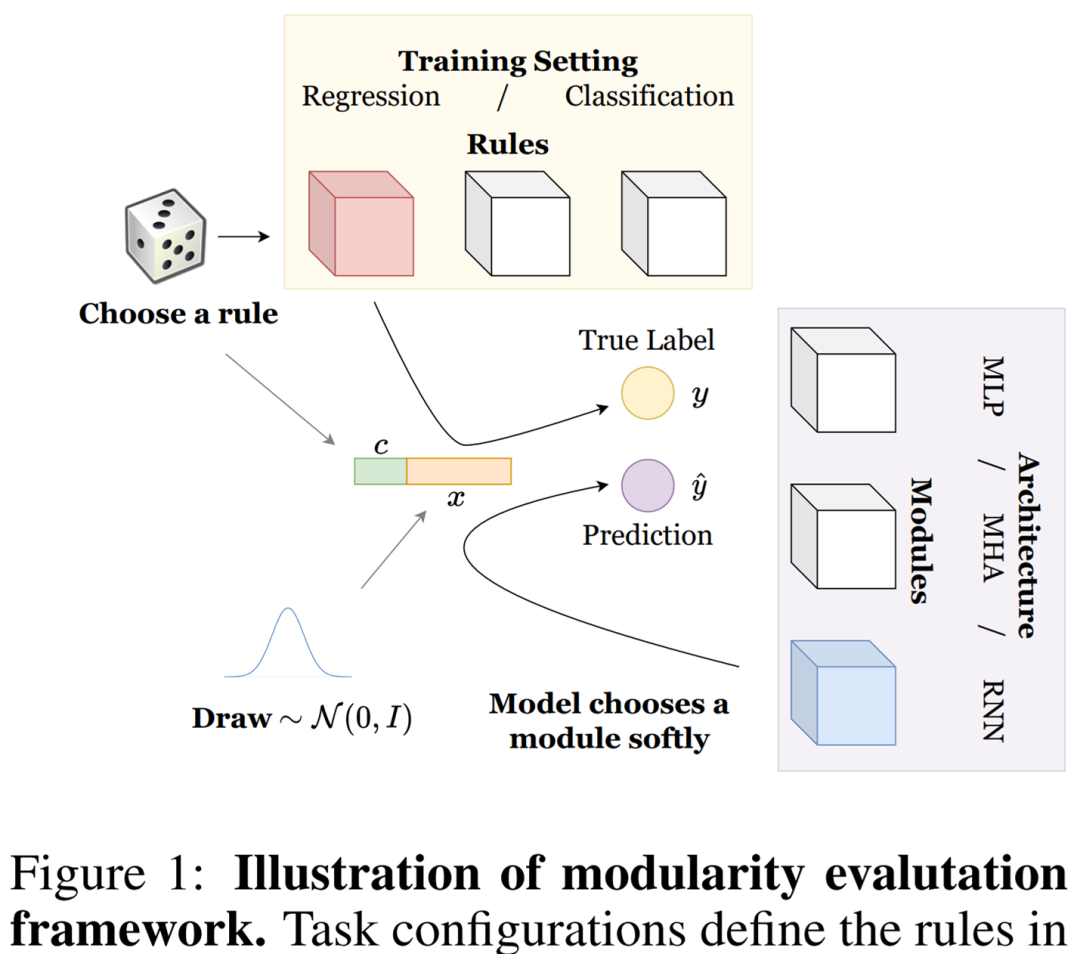
规则。为了正确理解模块化系统并分析它们的优缺点,研究者考虑采用的综合设置允许对不同的任务要求进行细粒度的控制。尤其是必须在如下公式 1-3 中展示的数据生成分布上学习操作,他们称之为规则。
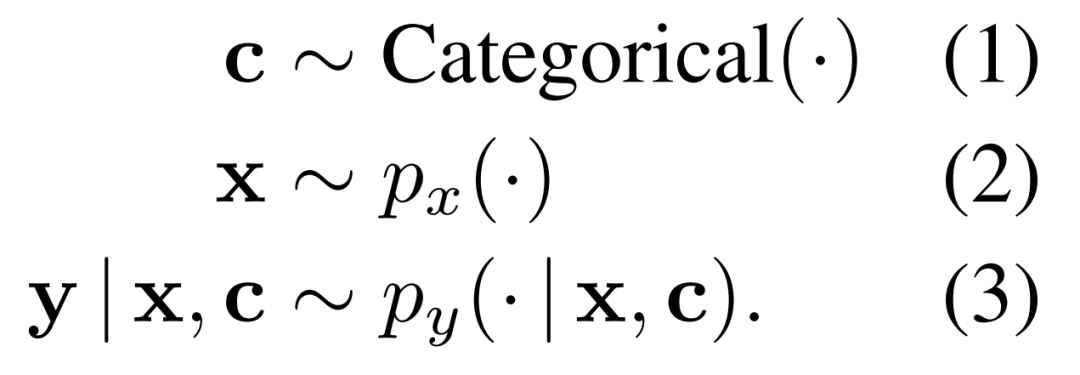
给定上述分布,研究者定义了一个成为其专家的规则,也即规则 r 被定义为 p_y(·|x, c = r) ,其中 c 是表示上下文的分类变量,x 是输入序列。
任务。任务是由公式 1-3 中展示的一组规则(数据生成分布)描述。不同的{p_y(· | x, c)}_c 集合意味着不同的任务。其中对于给定数量的规则,研究者在多个任务上训练模型以消除任何对特定任务的偏见。
模块。模块化系统由一组神经网络模块组成,其中每个模块都对整体输出做出贡献。通过如下函数形式可以看出这一点。
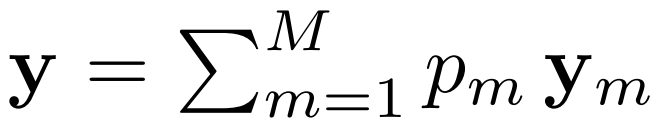
其中 y_m 表示输出,p_m 表示 m^th 模块的激活。
模型架构。模型架构描述了为模块化系统的每个模块或者单片系统的单个模块选择什么架构。在本文中,研究者考虑采用了多层感知机(MLP)、多头注意力(MHA)和循环神经网络(RNN)。重要的是,规则(或者数据生成分布)进行调整以适用于模型架构,比如基于 MLP 的规则。
数据生成过程
由于研究者的目标是通过合成数据来探究模块化系统,因此他们详细介绍了基于上文描述的规则方案的数据生成过程。具体地,研究者使用了简单的混合专家(MoE)风格的数据生成过程,希望不同的模块可以专门针对规则中的不同专家。
他们解释了适用于三种模型架构的数据生成过程,它们分别是 MLP、MHA 和 RNN。此外,每个任务下面都有两个版本:回归和分类。
MLP。研究者定义了适用于基于模块化 MLP 系统的学习的数据方案。在这一合成数据生成方案中,一个数据样本包含两个独立的数字以及从一些分布中采样的规则选择。不同的规则生成两个数字的不同线性组合以给出输出,也即线性组合的选择是根据规则进行动态实例化,如下公式 4-6 所示。


MHA。现在,研究者定义了针对模块化 MHA 系统的学习而调整的数据方案。因此,他们设计了具有以下属性的数据生成分布,即每个规则分别由不同的搜索、检索概念以及检索信息的最终线性组合组成。研究者在如下公式 7-11 中用数学方法描述了这一过程。
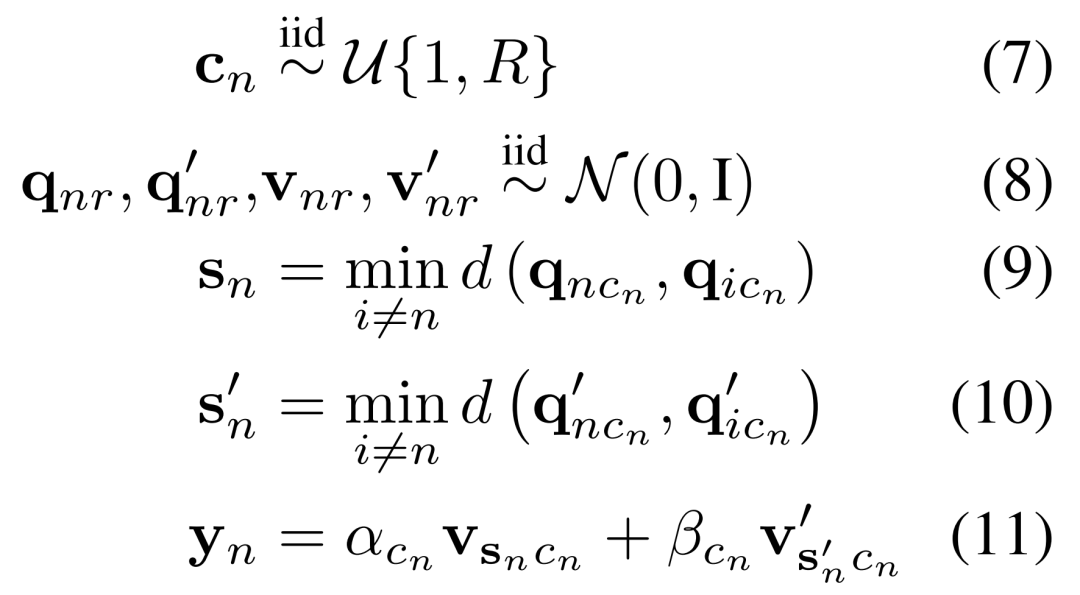
RNN。对于循环系统,研究者定义了一种线性动态系统的规则,其中可以在任何时间点触发多个规则中的一个。在数学上,这一过程中如下公式 12-15 所示。
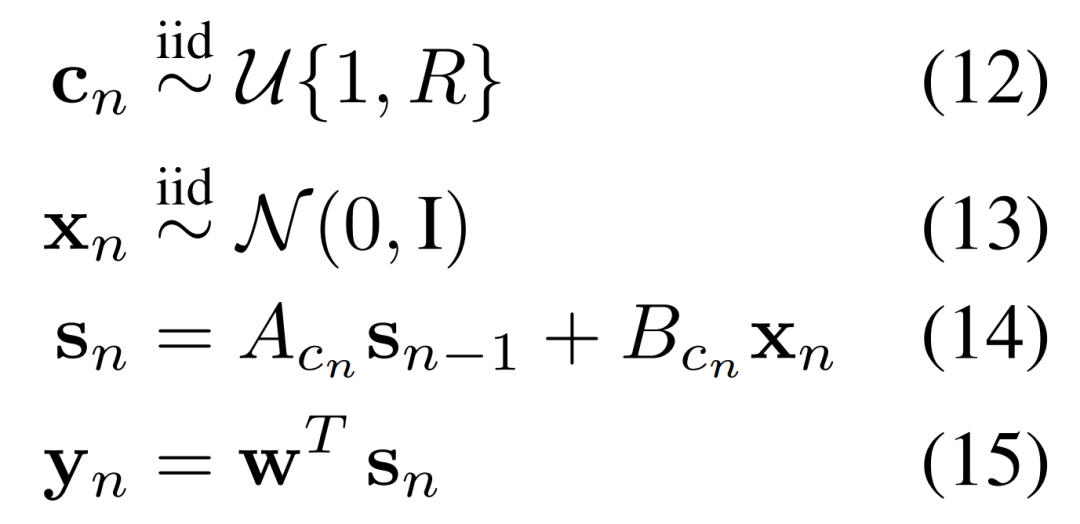
模型
以往一些工作宣称端到端训练的模块系统优于单体系统,尤其是在分布式环境中。但是,对于这些模块化系统的好处以及它们是否真的根据数据生成分布进行专业化处理还没有详细和深度的分析。
因此,研究者考虑了四类允许不同程度专业化的模型,它们分别是 Monolithic(单体)、Modular(模块化)、Modular-op 和 GT-Modular。下表 1 展示了这些模型。

Monolithic。单体系统是一个大型神经网络,它以整体数据 (x, c) 作为输入,并依此做出预测 y^。系统中显式 baked 的模块化或稀疏性没有出现归纳偏置,并完全取决于反向传播来学习解决任务所需的任何函数形式。
Modular。模块化系统由很多模块组成,每个模块都是给定架构类型(MLP、MHA 或 RNN)的神经网络。每个模块 m 将数据 (x, c) 作为输入,并计算输出 yˆ_m 和置信度分数,跨模块归一化为激活概率 p_m。
Modular-op。模块化操作系统与模块化系统非常相似,仅有一点不同。研究者没有将模块 m 的激活概率 p_m 定为 (x, c) 的函数,而是确保激活仅由规则上下文 C 决定。
GT-Modular。真值模块化系统作为 oracle 基准,即完美专业化的模块化系统。
研究者表明,从 Monolithic 到 GT-Modular,模型越来越多地包含模块化和稀疏性的归纳偏置。
度量
为了可靠地评估模块化系统,研究者提出了一系列度量,不仅可以衡量此类系统的性能优势,还能通过崩溃和专业化这两种重要的形式进行评估。
性能。第一组评估度量基于分布内和分布外(OoD)设置中的性能,反映了不同模型在各种任务上的表现。对于分类设置,研究者报告了分类误差;对于回归设置,研究者报告了损失。
崩溃。研究者提出了一组度量 Collapse-Avg 和 Collapse-Worst,以此来量化模块化系统遭遇到的崩溃量(也即模块未充分利用的程度)。下图 2 展示了一个示例,可以看到模块 3 未被使用。
专业化。为了对崩溃度量做出补充,研究者还提出了以下一组度量,即(1)对齐,(2)适应和(3)量化模块化系统获得的专业化程度的逆互信息。
实验
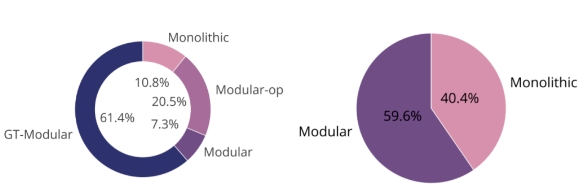
下图表明,GT-Modular 系统在大多数情况下都最优(左)的,这表明专业化是有益处的。我们还看到,在标准端到端训练的模块化系统和 Monolithic 系统之间,前者的表现优于后者但差距不大。这两个饼图共同表明,当前的端到端训练的模块化系统没有实现良好的专业化,因此在很大程度上是次优的。

然后,该研究查看特定架构选择,并分析它们在越来越多的规则中的性能和趋势。
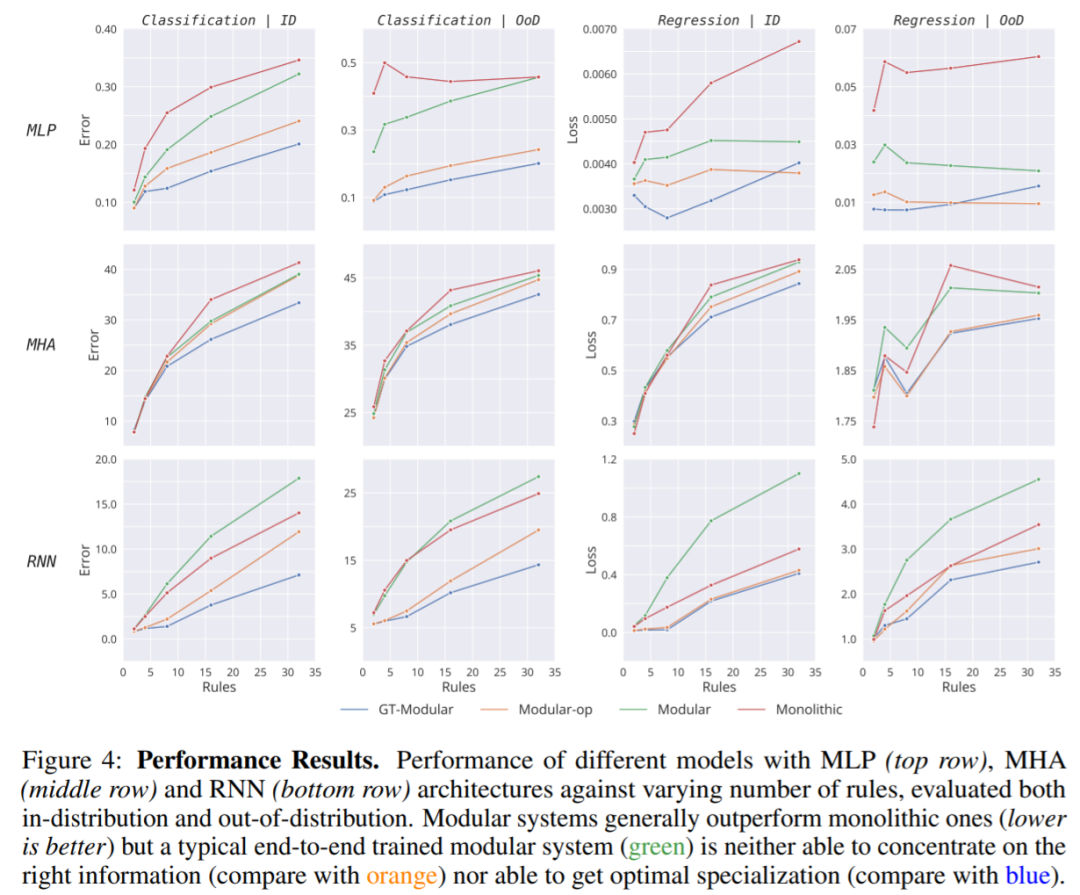
图 4 显示,虽然完美的专业化系统 (GT-Modular) 会带来好处,但典型的端到端训练的模块化系统是次优的,不能实现这些好处,特别是随着规则数量的增加。此外,虽然这种端到端模块化系统的性能通常优于 Monolithic 系统,但通常只有很小的优势。
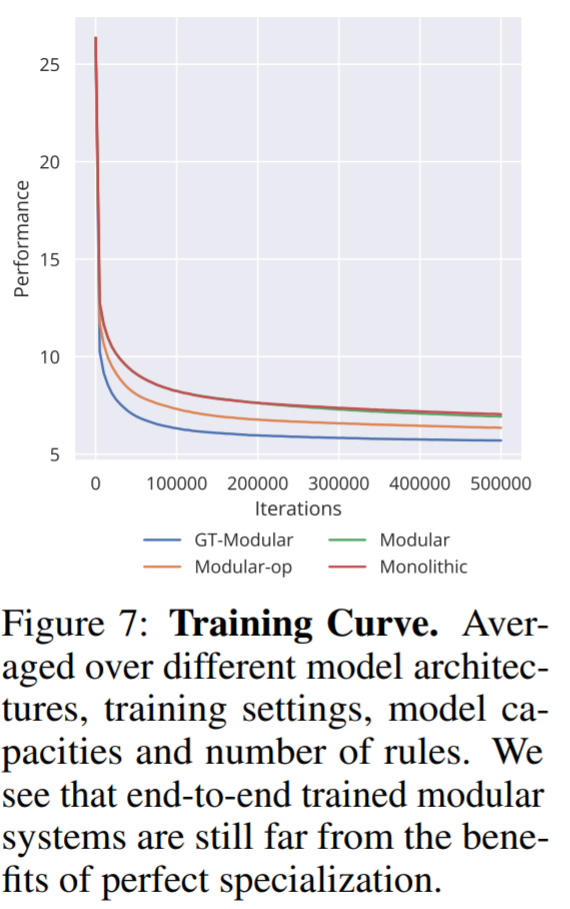
在图 7 中,我们还看到不同模型的训练模式在所有其他设置上的平均值,平均值包含分类错误和回归损失。可以看到,良好的专业化不仅可以带来更好的性能,而且可以加快训练速度。
下图显示了两个崩溃度量:Collapse-Avg 、Collapse-Worst。此外下图还显示了针对不同规则数量的不同模型的三个专业化指标,对齐、适应和逆互信息: