P/NP 问题是计算复杂度领域至今未解决的一个问题。人们一直试图找到一个问题的答案:「我们能否在合理时间内有效解决所有的计算问题?」
什么是合理的时间?实际上在宇宙终结之前能够解决的问题都算在合理时间内。然而许多问题似乎都难以在合理的时间内解决,这需要用数学来证明这些问题的难度。
2021 年的一项研究解答了上述问题,该研究证实:很大一部分问题都很难有效解决。
华盛顿大学的 Paul Beame 评价这项研究称:「就像攀登山峰一样,这项研究是计算理论研究路上的一个落脚点。」

该研究的三位研究者:计算机科学家 Srikanth Srinivasan(左)、Nutan Limaye(右上)和 Sébastien Tavenas。
该研究考虑的问题只涉及加法和乘法,但当这些问题仅限于以特定方式(加法和乘法的某种交替模式)解决时,它们就变得非常困难。
令人惊讶的是,该研究没有使用新的框架或工具,相反,作者设法绕过了由普林斯顿高等研究院数学学院教授 Wigderson 与耶路撒冷希伯来大学 Noam Nisan 合作数十年的工作中描述的数学障碍。
研究者之一、丹麦奥胡斯大学的 Srikanth Srinivasan 说:「我们意识到有一种非常简单的方法可以绕过这个障碍。并且,如果用这么简单的方法就能做到我们认为不可能的事情,那么肯定能找到更好的方法。」
重要的问题
计算机出现之后,科学家们发现计算机算法可以解决许多问题,但有时这些算法花费的时间太长——比实际计算时间更长。
他们开始怀疑有些问题是本质上难度太大,无论问题的规模是大是小都难以解决。例如在图中,一个重要的问题是确定是否存在一条哈密顿路径,即存在一条路径通过且仅通过每个顶点一次。增加点(和边)的数量应需要更长的时间来确定是否存在这样的路径,但即便是最好的算法,随着图规模的增加,花费的时间也会呈指数增长,这使得解决这个问题变得不切实际。
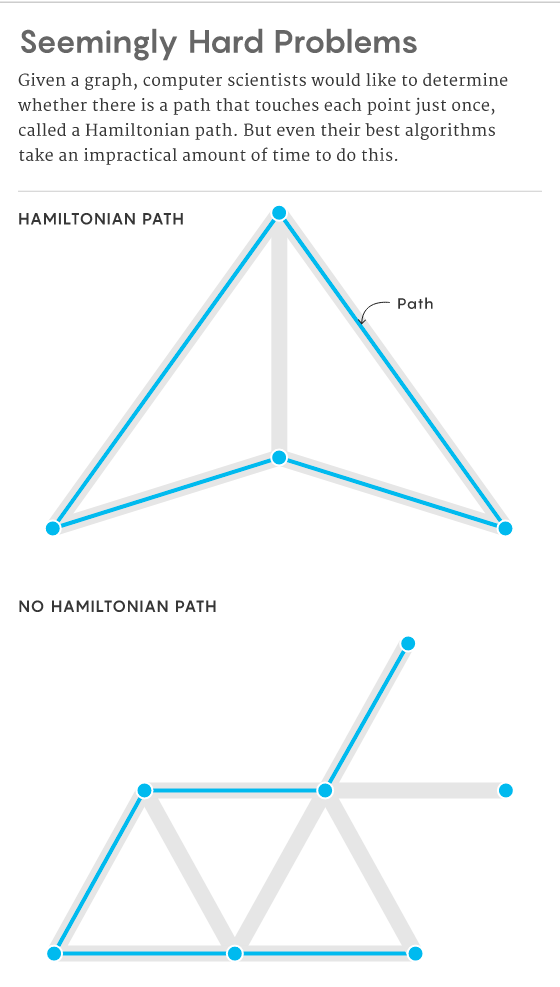
计算机科学家试图证明,任何能够以某种方式有效解决某类问题中一个难题的算法,都可以转化为对其他类似困难问题的解决方法,他们称这一类问题为 NP 问题。
当然,也有很多看起来不难的问题,不需要花费太多时间来解决。这些问题中的很多在某种意义上也是等价的,这类问题被称为 P 问题。他们认为 NP 问题确实比 P 问题更难,并且 NP 问题永远无法有效解决。但如果没有证据,这种想法就可能是错误的。
因此,计算机科学家们开始寻找方法来证明 NP 问题确实更难,这需要证明 NP 问题必须要指数级的时间才能解决,但证明这一点并不容易。
多难才算「困难(hard)」?
设想一组只需要加法和乘法的特定问题。例如,给定一组点,可以仅通过加法和乘法,用关于点的数据来计算所有可能的哈密顿路径(如果存在的话)。
随着问题规模的增加,一些算术问题(如计算哈密顿路径)需要更多的时间。1979 年,哈佛大学的 Leslie Valiant 证明许多算术问题在「难度」上是等价的,而其他的则在「没有难度」上是等价的。计算机科学家后来以他的名字命名这两类问题——分别是 VNP 和 VP。
和 P 与 NP 问题一样,我们无法证明 VNP 问题的难度,我们只知道 VNP 问题比 NP 问题更难,因为它建立在后者的基础之上,例如计算路径首先需要确定路径是否存在。
「这比 NP 难,因此证明这很困难应该更容易」,Shpilka 说道。
在随后的几十年中,计算机科学家在 VP 与 VNP 问题上取得的进展比他们在 P 与 NP 问题上取得的进展要大得多,但其中大部分仅限于 Valiant 创建的称为代数复杂性的子领域。在 Limaye、Srinivasan 和 Tavenas 最近的工作之前,他们仍然很难判断是否存在一般意义上的算术问题。
调整多项式
这项新工作有助于探究计算机科学家思考加法和乘法问题的方式。从数学上讲,这些问题完全可以写作多项式的形式(例如 x^2 + 5y + 6),这些多项式由相加和相乘的变量组成。
对于任何特定问题,例如计算哈密顿路径,你可以构建一个表示它的多项式。例如你可以用一个变量来表示每个点和边,这样当添加更多点和边时,就可以向多项式添加更多变量。
为了证明计算哈密顿路径这样的算术问题很困难,就需要证明当添加更多点和边时,相应的多项式需要以指数时间解决更多操作。例如,x^2 需要一次操作(x * x),而 x^2 + y 需要两次操作(x * x 然后加上 y)。操作的数量称为多项式的大小。
但是多项式的大小很难确定。例如多项式 x^2 + 2x + 1。它的大小似乎为 4(两次乘法和两次加法),但是该多项式可以重写为两个和的乘积,(x + 1)(x + 1),它的操作数更少——两次加法,一次乘法。通常,随着问题的规模扩大和将更多变量添加到多项式中,数学变换可以帮助简化和缩小其规模。
在 Valiant 的研究几年之后,计算机科学家找到了一种方法,可以使问题的大小更易于分析。为此,他们提出了一个称为「深度(depth)」的属性,它指定多项式在和与乘积之间切换或交替的次数。例如,多项式 x^2 + 2x + 1 的深度为 2,因为它是乘积之和(如 x^2 和 2x)。相比之下,表达式 (x + 1)(x + 1) 的深度为 3,因为它的深度与 0 + (x + 1)(x + 1) 相同,按照乘积之和计算。
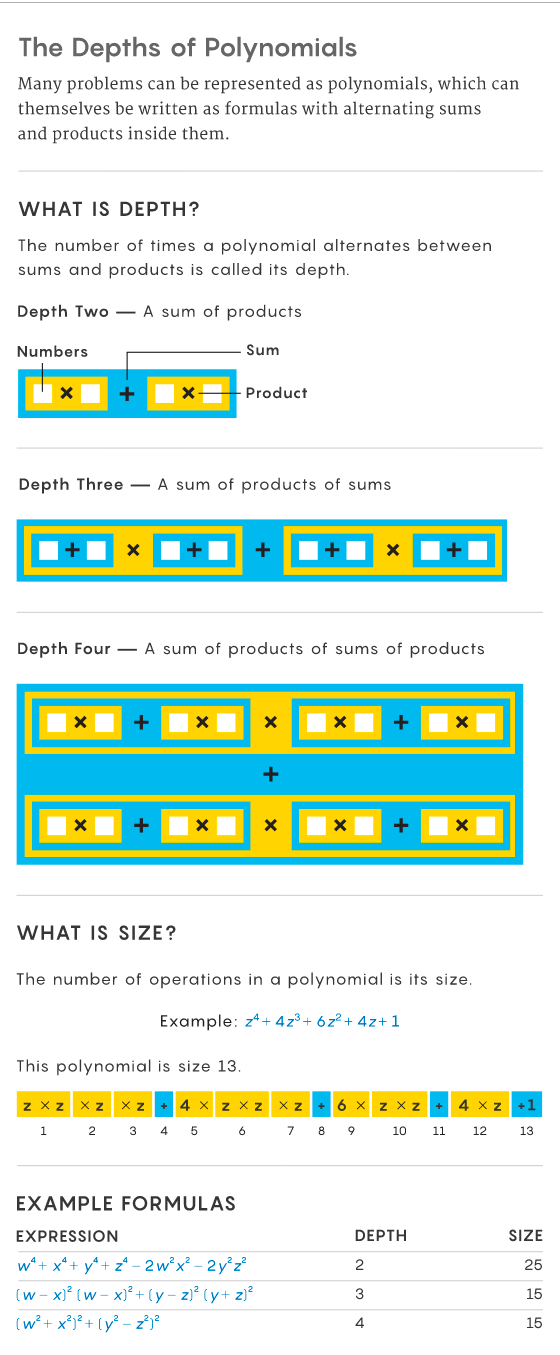
为了简化多项式,计算机科学家将它们限制为一种固定形式,并具有称为「恒定深度」的属性,其中和、乘积的模式不会随着问题的增长而改变。这使得它们的大小更加固定,多项式的大小会随着其深度的增加而减小。某个恒定深度的表达式称为公式。恒定深度让多项式的研究取得了更多进展。
神奇的「深度」
1996 年, Nisan 和 Wigderson 的一篇论文专注于解决矩阵乘法的问题,他们用两种方式简化了这个问题。首先,他们用恒定深度的公式来表示它——深度为 3。其次,他们只考虑了具有某种简单结构的公式,其中每个变量的最大指数为 1,这使得原问题成为「多线性」问题。
计算机科学家已经发现,某些问题可以转换为相对简单的集合多线性(set-multilinear)结构,代价是多项式的大小呈次指数增长(与指数增长的增长率相当)。
Nisan 和 Wigderson 随后表明了随着矩阵的扩大,矩阵乘法问题需要指数级的时间来解决。换句话说,他们证明了一个重要的问题是困难的,为证明一类问题都是困难的做出了努力。然而,他们的结果只适用于具有简单的、集合多线性结构的公式。

Leslie Valiant
增加多项式的深度往往会导致其大小减小。随着时间的推移,计算机科学家使这两个属性之间的权衡变得更精确。他们表明,将两个深度级别添加到深度 3、集合多线性多项式可以平衡其集合多线性结构的大小增益。如果深度 5 的结构化公式需要指数时间,那么具有一般、非结构化性质的深度 3 公式也是如此。
Srikanth Srinivasan 等人的新工作表明,矩阵乘法问题的深度 5 集合多线性公式确实以与指数级速度增长。这意味着一般的深度 3 公式也需要指数时间。随后他们证明类似的规律适用于所有深度(不止是 3 和 5)。有了这种关系,他们就证明了对于同一个问题,任何深度的一般公式的大小都会随着问题的规模而以指数速度增长。
他们还表明用一个恒定深度的公式表示矩阵乘法是很难的,无论该深度是多少。
该研究的结果首次提供了对于算术问题何时是「困难」的一般理解——当它不能用恒定深度的公式表示时即为困难。矩阵乘法的具体问题已知是 VP 问题。并且已知 VP 问题在不限于恒定深度时相对容易,因此结果得出恒定深度为问题「困难」的来源。
VNP 问题是否比 VP 问题更难?新结果并没有直接说明这一点,他们只表明恒定深度公式很难。但这仍然是证明 VNP 问题不能等价于 VP 问题的重要里程碑。
对于更大的 P 与 NP 问题,我们现在可以对有一天能找到答案更加乐观了。毕竟为了解决困难的问题,我们首先需要知道哪些方向是无望的。