前言
上次咱们聊了聊异或运算的妙用,其实简单来说,就是记住异或运算的三个特性
- 0和任何数N进行异或运算,结果为N。
- 任何数N和自己进行异或运算,结果为0。
- 异或运算满足交换律和结合律 当然如果您对这几个特性不是很了解,或者不是很熟悉异或运算的话,建议先看看这篇文章 位运算的妙用--异或运算。
「闲话不用多说,咱们来看面试真题」
Q1:一个数组中有一种数出现了奇数次,其他数都出现了偶数次,怎么找到这一个数
「要求:时间复杂度O(n)」。
其实这道题还是比较好理解的。
咱们直接来举例子。
比如数组[1,1,2,2,3] 把3找出来即可,因为3只出现了1次,为奇数次,其余的数字出现的都为偶数次。
比如数组[1,1,2,2,3,3,3] 同样把3找出来即可。
其实最简单的方法,也就是暴力破解法,咱们可以把数组循环一遍,把每个数字出现的数字记录在另一个数组中(需要记录数字和该数字出现的次数的map),然后循环另一个数组找出出现次数为奇数的即可。「但是这个题目有要求」,时间复杂度要求为O(n),也就是说只能循环一次就把结果就找出来,所以暴力破解法肯定是行不通的。所以咱们必须得换个思路。
利用异或运算的规律来解题
首先,在异或运算中「任何数N和自己进行异或运算,结果为0」,所以我们把数组中的所有数进行异或运算,所有「出现偶数次的数字进行异或运算结果为0」,咱们来看一个例子(因为异或运算满足交换律,所以不用关心数字出现的位置)。
arr = [a,b,b,c,c,c,c,d,d.]
比如看上述数组,咱们来对每个元素进行异或运算。
temp = a ^ b ^ b ^ c ^ c ^ c ^ c ^ d ^ d
因为「任何数N和自己进行异或运算,结果为0」所以除了a以外的数字,异或结果为0。
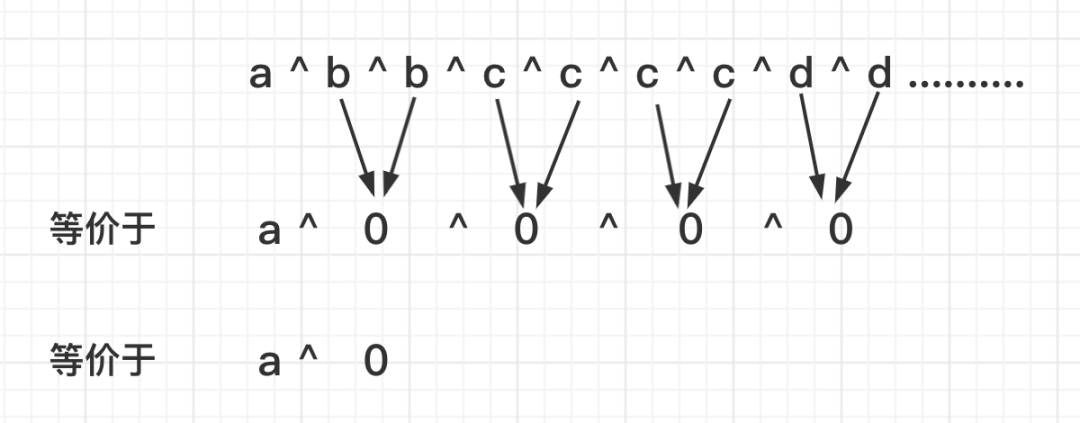
所以全部进行异或运算一次的结果为:
temp = a^0
其实简单的说就是两个b异或结果为0,两个c异或结果是0(上面的case写了4个c,其实结果是一样的),两个d异或结果为0,那么所有的数字异或下来,出现偶数次的结果异或运算的结果就为0。
另外根据「0和任何数N进行异或运算,结果为N」所以:
temp = a^0 = a
所以最终的temp则为我们需要找到的数,源码如下:
func findOddTimesNumber(arr []int) (temp int) {
for i := 0; i < len(arr); i++ {
temp ^= arr[i] //temp默认为0 相当于0^a(出现奇数次的数字)^b^b^c^c.......,根据上述运算的解析,结果为a,也就是我们想找到的数
}
return temp
}
如果上面的题您已经明白了,那么「接下来咱们加大难度,看一种更复杂的情况」。
Q2:一个数组中有两种数出现了奇数次,其他数都出现了偶数次,怎么找到这一个数
「要求:时间复杂度O(n)」。
这道题和上面那道题的区别就在于「有两种数字出现了奇数次」。
arr = [a,b,c,c,d,d,e,e]
其实简单说也就是要把上面数组arr中的a和b分别找出来,如果按照前面的方法全部异或一次,那么结果肯定为a^b,我们的目的是把a和b分别找出来,这种办法当然是行不通的,或者说是不够的。
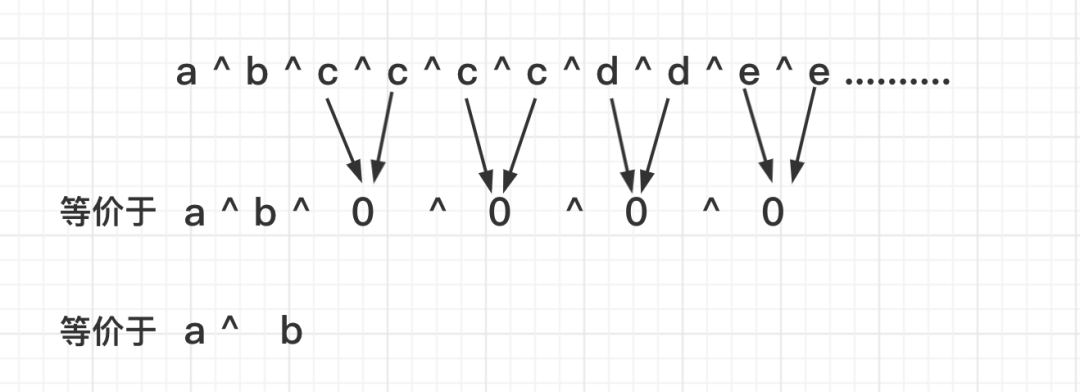
但是上面计算之后的结果:
temp= a^b(其余出现偶数次的数字进行异或运算结果都为0)
首先,因为a和b是两种数,所以「a肯定是不等于b的」,所以「a^b的结果肯定大于0」,换句话说a^b的结果,也就是「temp的二进制表现肯定是至少有一位是1的」。这句话很重要,明白了这句话咱们就继续往下看。
比如temp的第7位为1,那就说明a和b的第7位是不一样的,一个为0,一个为1。那么咱们是不是可以通过第7位是否为1,然后进行分组,「每个分组中出现的偶数次的数字的异或结果都是0的」,所以最后两个分组各自剩下的就是所需数字了。
咱们先来看一个方法。
res := num & (^num + 1)
上述方法的目的是获取num最左边的1。什么意思呢?比如num是 1011011,那么他最左边的1 就是00000001。
咱们用一个代入的方式一步一步的计算试试。

所以最后算法如下:
func findTwoOddTimesNumber(arr []int) (left, right int) {
for i := 0; i < len(arr); i++ {
left ^= arr[i]
}
temp := left & (^left + 1) //获取最左边的1
for i := 0; i < len(arr); i++ {
if arr[i]&temp == 0 { //根据某一位是否为1进行分组
right ^= arr[i]
}
}
left = right ^ left
return left, right
}