近日,剑桥学者在《美国科学院院报》(PNAS)上发表了一篇名为“The Difficulty of Computing Stable and Accurate Neural Networks: On the Barriers of Deep Learning and Smale's 18th Problem”的文章,提出了一个有趣的发现:
研究者可以证明存在具有良好近似质量的神经网络,但不一定存在能够训练(或计算)这类神经网络的算法。

论文地址:http://www.damtp.cam.ac.uk/user/mjc249/pdfs/PNAS_Stable_Accurate_NN.pdf
这与图灵的观点相似:无论计算能力和运行时间如何,计算机都可能无法解决一些问题。也就是说,哪怕再优秀的神经网络,也可能无法对现实世界进行准确的描述。
不过,这并不表明所有的神经网络都是有缺陷的,而是它们仅仅在特定情况下才能达到稳定和准确的状态。
研究团队通过引入一个经典逆问题,提出了一个分类理论,用来描述哪些神经网络可以通过算法进行计算,对「人工智能可以做什么和不可以做什么」这一历史性问题给出了一个新的答案。
同时,他们开发了一个新的模型——「快速迭代重启网络」(FIRENETs),能够在应用场景中同时保证神经网络的稳定性和准确性。一方面,FIRENETs 所计算的神经网络在对抗扰动方面具有稳定性,还能够将不稳定的神经网络变得稳定;另一方面,它在保持稳定性的前提下还取得了高性能和低漏报率。
以下是对该工作的简单介绍:
1 研究背景
深度学习 (DL) 取得了前所未有的成功,现在正全力进入科学计算领域。然而,尽管通用的逼近特性可以保证稳定的神经网络 (NN) 的存在,但当前的深度学习方法往往存在不稳定性。这个问题使得深度学习在现实生活中的落地充满危险。
比方说,Facebook(Meta)和纽约大学于2019年的 FastMRI 挑战赛中曾称,在标准图像质量指标方面表现良好的网络容易出现漏报,无法重建微小但具有物理相关性的图像异常。2020年 FastMRI 挑战赛将重点放在病理上,又指出:「这种虚幻的特征是不可接受的,尤其如果它们模拟的是正常结构,而这些结构要么不存在,要么实际上是异常的,那就非常有问题。正如对抗扰动研究所证明的,神经网络模型可能是不稳定的」。显微镜学中也存在类似的例子。
在不同的应用场景中,对误报率和漏报率的容忍度是不同的。对于具有高错误分析成本的场景,必须避免这种误报和漏报。因此,在医疗诊断等应用场景中,人工智能的「幻觉」可能存在非常严重的危险。
对于该问题,经典的近似定理表明,连续函数可以用神经网络很好地任意逼近。因此,用稳定函数描述的稳定问题往往可以用神经网络稳定地解决。这就产生了这样一个基础性问题:
为什么有些场景已被证明存在稳定、准确的神经网络,深度学习还会出现不稳定的方法和由 AI 生成的「幻觉」?
为了回答这个问题,研究者们启动了研究,希望确定深度学习在逆问题中所能达到的极限。
此外,深度学习中的神经网络还存在稳定性和准确性的权衡问题。稳定性差是现代人工智能的致命弱点,这方面也有一个悖论:尽管存在稳定的神经网络,但训练算法仍能发现不稳定的神经网络。这个基础性问题与Steven Smale 在1998年就人工智能极限提出的第18个数学问题有关。
计算稳定的神经网络并不困难,例如,零网络就是稳定的,但它准确度不高,因而不是特别有用。最大的问题是:如何计算既稳定又准确的神经网络?科学计算本身基于稳定性和准确性,然而,两者之间往往存在取舍,有时必须牺牲准确性以确保稳定性。
2 分类理论:计算稳定NN的算法的存在条件
针对上述问题,作者团队提出了一种分类理论,描述了达到一定准确度(且稳定)的神经网络可以被算法计算的充分条件。
他们从一个线性方程组欠定系统的经典逆问题出发:
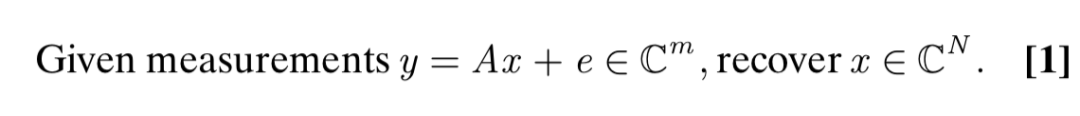
在这里,A∈Cm ×N 表示采样模型(m < N),比如 MRI 中的下采样离散傅里叶变换,x表示未知量。矢量 e 对噪声或扰动进行建模。该方程 1 所展示的问题是许多逆问题和图像分析的基础。
基于定理1和定理2(定理详情见论文),他们指出这样一个悖论性问题:
存在从训练数据到合适的神经网络的映射,但没有训练算法(即使是随机的算法)可以从训练数据中计算神经网络的近似值。
对此,该论文的其中一位作者Hansen做了一个类比:「可能存在一种蛋糕,但却不存在制作它的配方」。他认为,问题不在于「配方」,而是在于制作蛋糕所必须的「工具」,有可能无论你使用什么搅拌机,都无法制作出想要的蛋糕,但在某些情况下,也有可能你自家厨房里的搅拌机就足够了。
那么是在什么情况下呢?研究团队对计算神经网络的算法进行了分类,解释了什么条件下计算神经网络的算法才会存在(这也可以类比为:哪些蛋糕可以用具有物理设计可能性的搅拌机来制作):
定理2
计算神经网络的算法是否存在取决于期望的精度。对于任意正整数 K > 2 和 L,存在良态问题类,同时有以下情况:
a)不存在随机训练算法(即便是随机的算法)能以超过 50% 的概率计算出具有 K 位精度的神经网络;
b)存在一种确定的训练算法,可以计算具有 K-1 位精度的神经网络,但需要大量的训练数据;
c)存在一种确定的训练算法,可以使用不超过 L 个训练样本计算具有 K-2 位精度的神经网络。
这表明,一些基础性的、本质性的障碍阻止了神经网络被算法计算。这也是为什么一些场景中存在稳定而准确的神经网络,但深度学习仍会出现「幻觉」的原因。
3 FIRENETs:平衡稳定性与准确性
神经网络的稳定性与准确性之间存在权衡问题,一个稳定的神经网络在逆问题中的性能表现往往是有限的。这在图像重建中尤其突出,当前深度学习重建图像的方法会出现不稳定性,这体现在:
1)在图像或抽样域中的一个微小扰动就可能在重建图像中产生严重的伪影;
2)图像域中的一个微小细节可能会在重建图像中被洗掉(缺乏准确性),导致潜在的漏报。
这类线性逆问题导致深度学习方法在稳定性与准确性之间的不平衡,使得任何图像重建方法都无法在不牺牲准确性的情况下保持较高的稳定性,反之亦然。
为了解决这个问题,研究团队引入一种「快速迭代重启网络」(FIRENETs)。经证明与数值验证,FIRENETs 十分稳定。他们发现:在特定条件下,比如在 MRI中 ,有一些算法可以为方程1中的问题计算稳定的神经网络。
关键是,他们证明了 FIRENETs 对扰动具有鲁棒性,甚至可用来使不稳定的神经网络变得稳定。
FIRENETs对扰动具有鲁棒性
在稳定性测试中,团队将 FIRENETs 与V. Antun等人(2020)开发的AUTOMAP网络进行对比。如下图中的上行所示,AUTOMAP网络重建很不稳定,导致图像完全变形。下行则是使用FIRENETs网络的重建结果。即使在最差的重建结果中,它仍然保持稳定。
这证明了由FIRENETs算法所计算的神经网络在小波中稀疏的图像中,在对抗扰动方面具有稳定性,而且同时能够维持一定的准确性。
FIRENETs的稳定器作用
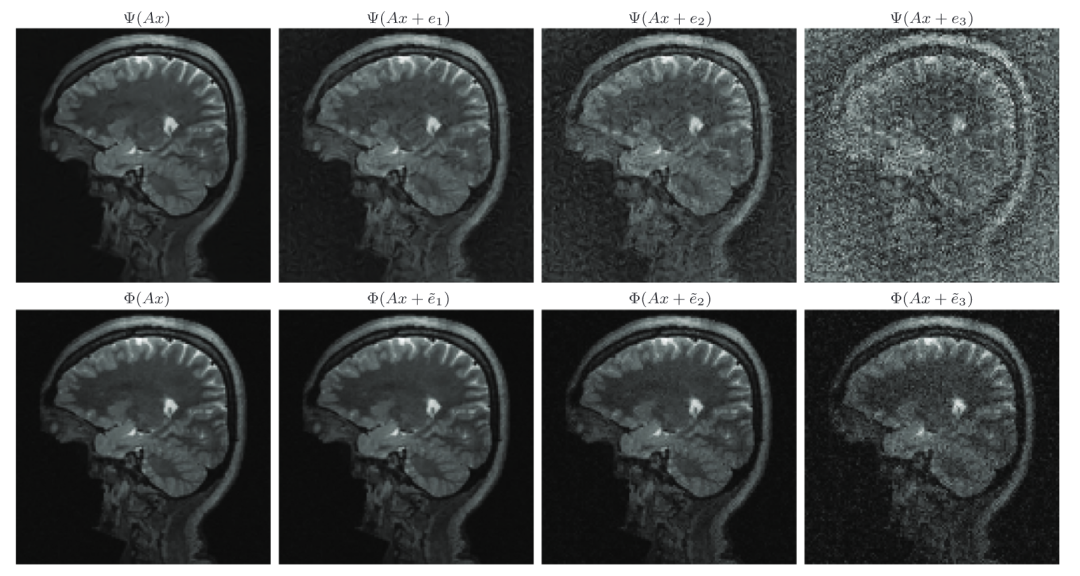
同时,FIRENETs也起到了一个稳定器的作用。比如在下图中,将来自AUTOMAP的重建输入到FIRENETs,结果显示,FIRENETs修正了AUTOMAP的输出并将重建加以稳定化。

图注:在AUTOMAP 的末端添加一些FIRENET层使其稳定。最左边是AUTOMAP的重建。左二是x0 = Ψ( ̃y)的FIRENET 的重建。右二是 ̃y = Ax + e3时FIRENET 的重建。最右边是输入AUTOMAP 的测量值后FIRENET的重建。
FIRENETs兼具稳定性与准确性
在下图中,一个在包含椭圆形状的图像上训练的 U-Net 很稳定,但是,当添加一个原先不包含在训练集中的细节后,U-Net 的稳定性就会受到极大影响。
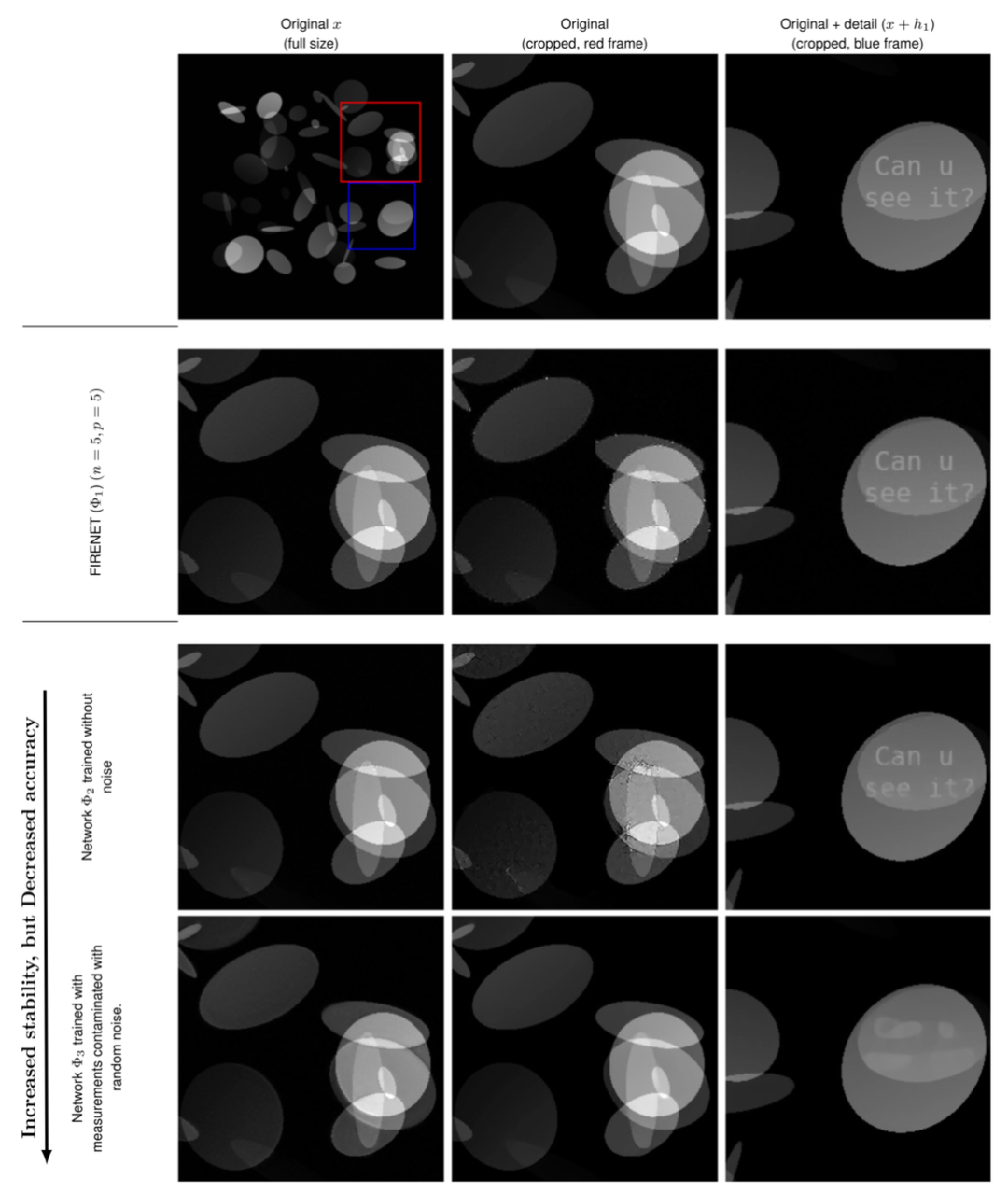
图注:性能有限的神经网络经过训练是可以具有稳定性的。考虑三个重建网络Φj : Cm → CN , j = 1, 2, 3。对于每一个网络,计算一个扰动值wj∈CN,旨在模拟最坏的效果,并在左列展示了一个经裁剪的摄动图像x + wj (第二至四行)。中间一列(第二至四行)显示了每一个网络的重建图像 Φj(A(x + wj))。在右列,以“Can u see it?”的文本形式测试了网络对微小细节h1的重建能力。
可以看到,在有噪声测量值条件下训练的网络对于最坏情况下的扰动保持稳定,但并不准确。相反,无噪声训练的网络是准确的,但不稳定。而FIRENET实现了二者的平衡,对于小波稀疏且在最坏情况下的稳定图像来说,它仍是准确的。
但这并不是故事的结局,在现实生活中的应用场景中,找出稳定性与精度之间的最优权衡是最重要的,这无疑需要无数种不同的技术来解决不同的问题和稳定性误差。