单链表的常见操作比较多，而且有些操作比较有技巧，本文就来聊聊这些不容易想到操作。
单链表倒数第 k 个节点
单链表正向第 k 个节点很容易获得，直接一个 for 循环遍历一遍链表就能得到，但是如果是逆向第 k 个节点，也就是倒数第 k 个节点呢 ?
你也许很快就想到了，逆向第 k 个节点相当于正向第 n - k 个节点, 这里的 n 是链表长度，对于单链表来说，需要遍历一遍链表才能计算出 n 的值，然后再次遍历 n - k 个节点, 才最终获得链表倒数第 k 个节点。
上面整个过程总共遍历了 n + n - k 个节点，能否只遍历 n 个节点就能得到倒数第 n 个节点呢 ?
答案是肯定的，这种解法称作 双指针法，它比较巧妙，如果以前没接触过过的话，不容易想到，下面就来详细介绍它。
假如 k = 2, 现在让指针 p1 指向 head 节点，然后移动 k 步，结果如下图：
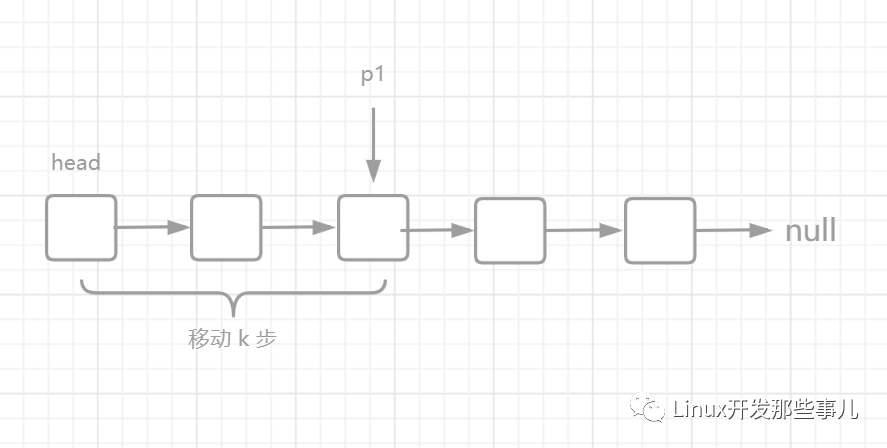
此时，如果 p1 再移动 n - k 步就到达链表结尾的 null 节点了。
再用一个指针 p2 指向 head 节点，指针 p1 和 p2 的指向如下图所示：
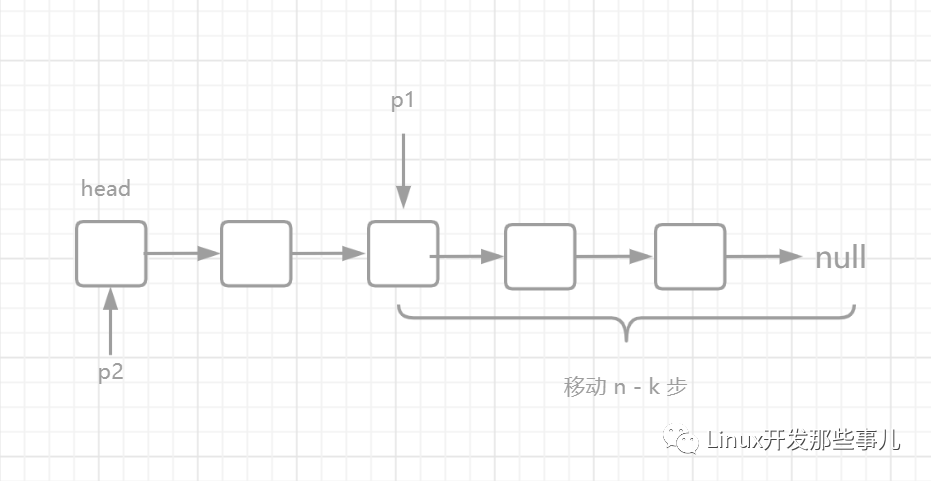
最后，指针 p1 和 p2 同时向前移动，直到 p1 到达链表结尾的 null 节点，此时两个指针的指向如下图所示：
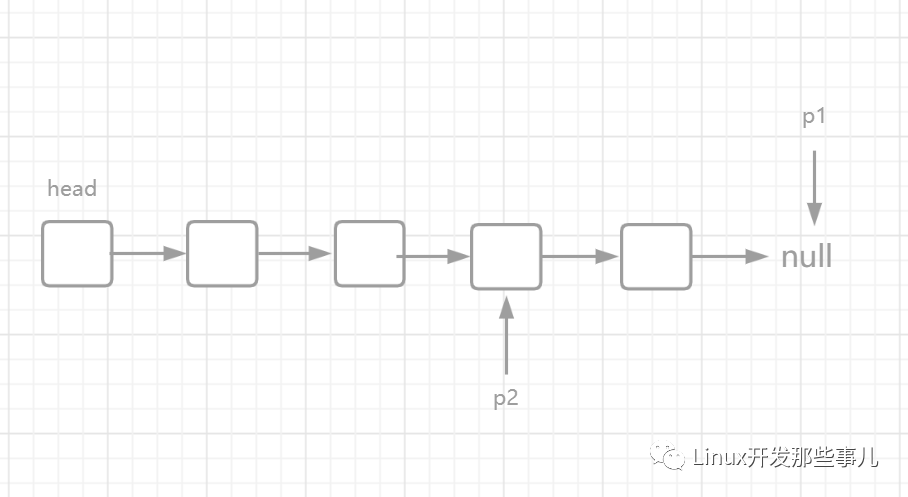
当 p1 到达 null 节点时，p2 走了 n - k 步，也就是倒数第 k 个节点。
这样，利用 p1 和 p2 两个指针，只需要遍历一遍链表就能得到倒数第 k 个节点，也即 p2 指向的节点。
在整个过程中，使用了两个指针，所以这个技巧称作 双指针法，很多链表相关的算法题都可以用这个技巧解决，理解了这个套路，以后再遇到类似的问题就可以手到擒来了。
好了，流程讲完了，下面给出完整代码供大家参考：
// 单链表节点结构
struct ListNode
{
int val;
ListNode *next;
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *pnext) : val(x), next(pnext) {}
};
// 返回单链表倒数第 k 个节点
ListNode *findFromEnd(ListNode *head, int k)
{
if(nullptr == head || k <= 0) return nullptr;
ListNode *p1 = head;
// p1 指针先移动 k 步
int step = 0;
while (step < k && nullptr != p1)
{
p1 = p1->next;
++step;
}
//p1 移动的步数小于 k, 表示链表长度小于 k
//因此链表不存在倒数第 k 个节点
if (step < k) return nullptr;
//p1 和 p2 同时移动，直到 p1 到达尾节点的下一节点
ListNode *p2 = head;
while (nullptr != p1)
{
p2 = p2->next;
p1 = p1->next;
}
return p2;
}
单链表中点
想得到单链表的中点，首先想到的是先得到链表的长度 n，然后从链头开始往前走，每走一步，计数就加一，直到计数达到链表长度的一半儿 n / 2，此时所在的节点即为链表的中点了。
但是这个方法需要先遍历整个链表，然后再从链表头遍历到链表的中间节点，整个过程共遍历了 n + n / 2 个节点。
这里介绍一种方法，只需要遍历 n 个节点就可以得到链表的中间节点。
我们让指针 p1 和 p2 都指向 head 节点，两个指针同时向前移动，p1 每次向前走两步，p2 每次向前走一步，这样，当 p1达到链表尾节点时，p2 刚好到达链表的中间节点。
在这个过程中，p1 指针每次走两步，称为快指针，p2 指针每次走一步，称为慢指针，所以，这个小技巧叫做 快慢指针。
根据上面的思路，我们就可以写出算法的实现代码了。
// 单链表节点结构
struct ListNode
{
int val;
ListNode *next;
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *pnext) : val(x), next(pnext) {}
};
// 返回单链表中间节点
ListNode * middleNode(ListNode *head)
{
if(nullptr == head) return nullptr;
//快指针和慢指针初始都指向head
ListNode *pslow = head;
ListNode *pfast = head;
while (nullptr != pfast && nullptr != pfast->next)
{
//每次快指针走两步，慢指针走一步
//当快指针的下一个节点为 null时
//表示快指针达到了末尾节点,此时退出循环
pfast = pfast->next->next;
pslow = pslow->next;
}
return pslow;
}
需要说明一点，如果单链表长度为偶数，也就是中间节点有两个，上面的解法返回的是靠后一个节点。
例如: 单链表 1 -> 2 -> 3 -> 4 -> 5 -> 6，长度为 6，它的中间节点是 3 和 4，那么，用上面的解法得到的中间节点是 4 而不是 3。
链表是否包含环
如下图所示，图中是一个长度为5的链表，最后一个节点指向了第三个节点，构成了一个环。
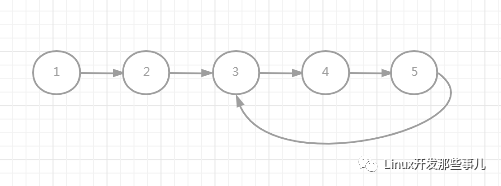
给你一个单链表的头节点，判断该链表是否含有环。
如何判断单链表存在环呢 ?我们可以借用 单链表的中点 问题的思路。
快慢指针同从头节点同时向前移动，在没有环的单链表中，它们依次达到尾节点，但对于有环的链表来说，快慢指针最后会一直在环中移动，永远停不下来。
由于两个指针一块一慢，并且快指针每次比慢指针多走一步，因此，快指针总有一天会追上慢指针，此时它俩就指向同一个节点，明白了这一点，就有办法判断单链是否存在表环了，具体做法如下：
初始时，快慢指针都指向头节点，它们同时向前移动，快指针每次走两步，慢指针每次走一步，当快指针和慢指针相等时，说明链表有环，如果快指针的下一个节点是 null 节点，表示链表没有环。
根据上面的思路，就可以写出实现代码了。
//返回单链表是否存在环
bool hasCycle(ListNode *head)
{
if(nullptr == head) return false;
//快指针和慢指针初始都指向head
ListNode *pslow = head;
ListNode *pfast = head;
while (nullptr != pfast && nullptr != pfast->next)
{
//快指针每次走两步，慢指针每次走一步
//当快指针的下一个节点为 null时
//表示快指针达到了末尾节点
pfast = pfast->next->next;
pslow = pslow->next;
if (pfast == pslow)
{
return true;
}
}
return false;
}
链表环的起始节点
我们再深入下，既然解决了链表是否有环的问题，那能不能知道环的起始节点呢 ?
比如: 对于下图中的链表来说，环的起始节点是 3。
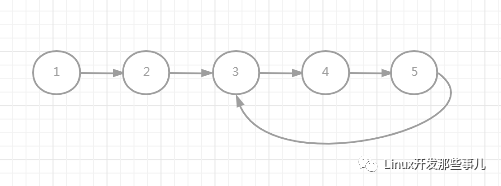
解决的方法依然是使用快慢指针，快指针每次走两步，慢指针每次走一步。
下图是一个简易的环形链表图，其中 A 为链表头节点，B 为环的起始节点，C为 快指针和慢指针在环中相遇的节点(至于快指针和慢指针为什么一定会在环中相遇，在上一小节有解释，这里不在赘述了)。
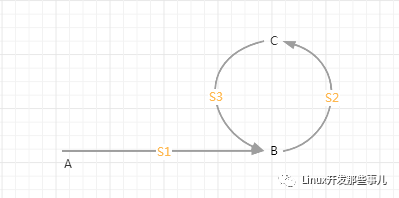
A 到 B 的距离是 S1。
B 到 C 的距离是 S2。
C 到 B 的距离是 S3。
假设，当快指针和慢指针在 C点相遇时，快指针已经绕着环走了 n 圈，则相遇时各自走过的路程如下：
快指针: S1 + n * ( S2 + S3 ) + S2。
慢指针：S1 + S2。
由于快指针走过的路程是慢指针的 2 倍，则有：
S1 + n * ( S2 + S3 ) = 2 * (S1 + S2)
简化下上面的等式可以得到:
S1 = (n - 1) * (S2 + S3) + S3
S2 + S3 刚好是环的长度，所以，上面的结果可以理解为，从 A 到 B 的距离，等于从相遇点 C 出发，绕着环走 n - 1圈 ( 此时会回到 C 点 ) ，然后再走 S3 就到达了 B 点，也即环的起始点。
因此，当快慢指针相遇后，再额外使用一个指针指向链表头节点，然后这个额外指针和慢指针同时移动，它们最终一定会在环的起始节点相遇。
搞明白了上面的推理过程之后，实现代码直接在 链表是否存在环 那一小节的基础上稍作修改即可，具体的代码如下：
//返回单链表环的起始节点
ListNode *entrynodeInLoop(ListNode *head)
{
if (nullptr == head || nullptr == head->next)
return nullptr;
ListNode *pslow = head; //慢指针
ListNode *pfast = head; //快指针
ListNode *ppoint = nullptr;//指向快慢指针相遇时的节点
while (nullptr != pfast && nullptr != pfast->next)
{
pslow = pslow->next;
pfast = pfast->next->next;
if (pslow == pfast)
{
ppoint = pslow;
break;
}
}
//相遇节点为null,表示没有环
if (nullptr == ppoint) return nullptr;
pslow = head; //慢指针指向头节点
while (pslow != ppoint)
{
pslow = pslow->next;
ppoint = ppoint->next;
}
return ppoint;
}
其实，链表是否有环 以及 链表环的起始节点 还有一种比较直观的求解方法。
额外增加一个记录节点指针的集合，然后从头节点开始往前遍历，每经过一个节点，查询集合中是否已存在该节点，如果不存在，节点指针加入到集合中，如果存在，则表示该节点就是环的入口节点。
这种方法比较好理解，但是它的空间复杂度是 O(N), 时间复杂度跟 快慢指针 相同，这里也给出实现代码供参考。
//返回链表环的起始节点
ListNode *entrynodeInLoop(ListNode *head)
{
if(nullptr == head) return nullptr;
//链表节点的集合
unordered_set<ListNode*> setnode;
ListNode *p = head;
while (nullptr != p)
{
auto iter = setnode.find(p);
if( iter != setnode.end())
{
//集合中找到了相同的节点
//此节点即为环的入口
return p;
}
//节点不在集合中，则加入集合
setnode.insert(p);
//移动到下一个节点
p = p->next;
}
//不存在环，返回 nullptr
return nullptr;
}
两个链表是否相交
给你两个链表的头节点，如果这两个链表相交，则返回相交的节点，如果没相交，返回 null。
比如下图中，两个链表相交的节点是 3。
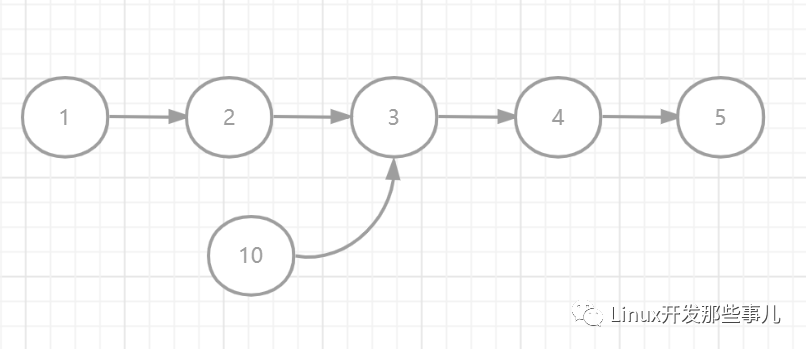
初看这个问题，最容易想到的方法是分别遍历两个链表，用一个集合记录遍历过程中的节点，如果存在相交的节点，肯定会多次访问该节点，当第二次访问该节点的时候，集合中已经存在该节点了，如果没有相交，则集合中不会出现两个相同的节点。
但利用集合临时存储遍历过的节点的方法，空间复杂度是 O(N)，如何在 O(1) 的空间复杂度内解决呢?
解决方法是利用两个指针p1 和 p2，初始时 p1 指向第一个链表的头节点，p2指向第二个链表的头节点，然后同时开始遍历链表，p1 遍历完链表之后，指向第二个链表的头节点，p2 遍历完链表之后，指向第一个链表的头节点。
实际上相当于两个链表连在一起了，具体看下图：
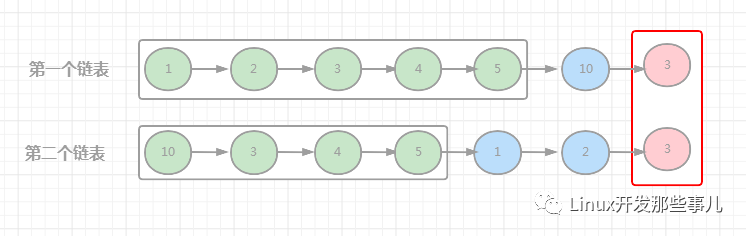
图中绿色的节点是当前链表的节点，蓝色的节点是对方链表的节点，红色的是遍历过程中相遇的节点，也即两个链表相交的节点，当两个链表没有相交时，最后p1 和 p2 都指向了空节点，这也是我们想要的结果，大家可以自己模拟下这个过程。
因此，此题的关键是找到一种办法，使得 p1 和 p2 能同时到达两个链表相交的节点。
根据上述的方法，可以写出实现代码 :
// 单链表节点结构
struct ListNode
{
int val;
ListNode *next;
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *pnext) : val(x), next(pnext) {}
};
//返回两个链表相交的节点
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB)
{
if (nullptr == headA || nullptr == headB)
return nullptr;
ListNode *pa = headA;
ListNode *pb = headB;
while (pa != pb)
{
pa = (nullptr != pa) ? pa->next : headB;
pb = (nullptr != pb) ? pb->next : headA;
}
return pa;
}
小结
本文讲解了链表相关的一系列操作，有些方法比较有技巧性，一时不太容易想到，需要大家多去体会和练习，假以时日，我相信大家一定能掌握并熟练使用这些套路的
