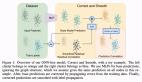
脉冲神经网络（Spiking Neural Network, SNN）被誉为第三代的神经网络，以其丰富的时空领域的神经动力学特性、多样的编码机制、事件驱动的优势引起了学者的关注。由于生物合理性与任务需求间存在不同程度的取舍，对网络使用的神经元模型、编码方式等各有差异，这造成了 SNN 的多样化。
与向量乘法为基础的传统人工神经网络（ANN）不同，SNN 通过模拟大脑的功能结构，以神经元为计算、存储单元，通过累积在膜电压上由相邻神经元发出的脉冲信号，并在超过阈值电位时发射脉冲的方式传递信息。由于其计算可以完全由加法完成，需要的计算量和功耗大幅减少。此外，由于 SNN 中神经元的执行、学习机制，使得 SNN 与一些新兴器件天然结合在一起。
论文链接：https://www.aaai.org/AAAI22Papers/AAAI-364.LiuF.pdf
脉冲神经网络的目标是在基于异步电路的实现，每个神经元可以异步接收和发射脉冲信号。然而这种大规模的异步电路目前还无法实现，脉冲神经网络中的所有脉冲信号需要对齐至时钟信号。这样做会带来两个问题：其一，为了精确表达脉冲发射的时间，需要将一次推理分割成大量的时间步(time step)，使得脉冲序列变的十分冗长；其二，脉冲序列中的脉冲数量没有变化，使得脉冲序列出现不规则的稀疏脉冲。现有的同步脉冲神经网络芯片，例如 Loihi，在一定程度上利用了稀疏性。但是，时间步增加导致的推理时间延长问题依然存在。
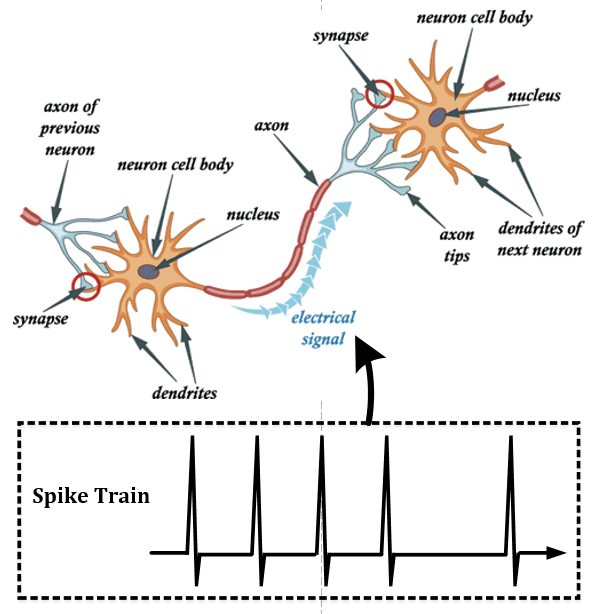
现有的脉冲神经网络的训练方法分为两种方法：直接训练和通过传统神经网络转换得来。直接训练的 SNN：可以进一步划分为有监督训练和无监督训练。有监督训练的 SNN 是基于脉冲的反向传播算法，然而神经元函数不可微，导致传统的反向传播算法没办法直接应用在 SNN 上。无监督训练的 SNN 是利用突触可塑性规则的仿生学习算法。
例如：脉冲时序依赖的突触可塑性（Spike-Timing Dependent Plasticity, STDP）是最具代表性的无监督 SNN，根据神经元激发的先后顺序，调整神经元之间连接的强弱。基于转换的 SNN：为了在已发展的深度学习成果上进一步利用脉冲神经网络低能耗的特点，从 ANN 的视角出发，将连续的激活函数值通过 SNN 中频率编码下的平均脉冲发放率进行替代，并且使用神经元函数替换 ANN 中的 ReLU 函数，再通过特定手段将其转换为 SNN。
从本质上说，基于转换的 SNN 其训练仍然依赖于 ANN 中的反向传播算法，因此它避免了对 SNN 进行直接训练的困难。就性能表现而言，基于转换的 SNN 保持着与 ANN 发展相匹配的进程。
然而，现有的 SNN 在实现超大规模的网络结构上，仍然面临梯度消失、训练资源开销大甚至算法收敛性的问题，一般只能应用在浅层的 SNN 中，并且精度还距离 ANN 有一定的差距。而现有的转换方法应用在更深的网络或更复杂的数据集时，需要大量的时间步长表示脉冲序列（例如：在 ImageNet 中，VGG 转换而来的 SNN 需要的时间步数量高达 2048[3,4]）。
相比于进行一次 ANN 的推理只需要执行一次前向传递过程；SNN 在每个时间步都需要执行一次前向传递。因此，时间步的数量过多会引入极大的推理延迟，导致了转换后的 SNN 网络难以胜任对实时性有要求的应用。
方法介绍
本文提出一种基于高效且准确的 ANN-SNN 转换框架，不仅可以应用到传统神经网络的最新发展，而且大幅度降低了时间步的数量。只需要 8-16 个时间步就可以达到和传统神经网络几乎一致的精度，节省了百倍的时间延迟。
转换中的一致性关系
首先，我们在神经元发射脉冲之后采用了软重置的策略，在当前的膜电位中减去阈值电位的值，从而保留了超出阈值的部分。在之前的大部分文章中，采用的是硬重置策略，当膜电压超过阈值时发射脉冲并将膜电压直接重置为 0。这样做的好处是尽可能多的保留了膜电压中包含的信息，并且能够在输入的微小扰动下保持相对一致的输出结果。软重置方法可以用公式表达为
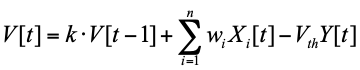
其中 V[t]是 t 时刻的膜电压，k 是每个时间步之间的膜电压衰减系数。Xi 是第 i 个相邻神经元的脉冲序列，0 表示 t 时没有脉冲传输。Y 是当前神经元的输出脉冲序列。将公式 (1) 在 t=1 到 T 累加，我们可以得到
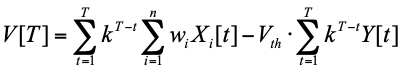
在理想情况下，最后神经元内没有膜电压存留，即 V[T]=0。此时，公式 (2) 可以简化为
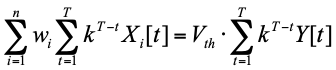
不难发现，公式 (3) 与传统神经网络的 MAC 计算模式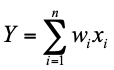
十分相似，而事实上之前最为常用的基于 ANN 转换的 SNN，将 ANN 的激活值作为 SNN 中的神经元发射脉冲的频率，正是公式 (3) 在 k=1 的特例。
然而，公式 (3) 在很多情况下并不成立。最明显的一种情况，是膜电压在最后并不一定会等于 0 或一个相对较小的数。事实上，由于神经元之间的权重有负值，导致很多时候膜电压最终是一个负数。SNN 的神经元模型的机制决定了其只会对正的电压做出反应而累积的负膜电位则会被保留，从而导致公式 (3) 的等号并不成立，信息无法准确表达，使得脉冲神经网络的精度低于传统神经网络。
例如当 k=1 以及阈值电位 = 1 的情况下，如果输入总膜电位分别为 1,1,-1,-1，则会在前两个时间步产生脉冲信号；而后两个 - 1 则被累积在膜电位中无法消耗。此时公式左边 = 0 而右边 = 2，公式并不成立。
神经元计算中的时域分离
针对这一点，文章采用了时域分离的方法，将膜电压的累积过程和膜电压释放脉冲的过程在时域上分离开，避免膜电压累积信息丢失的情况出现。为了实现时域分离的效果，即发射脉冲在累积电压之后，应使得较晚时间的膜电压在没有额外输入的情况下要大于之前的膜电压。这在之前的 leaky integrate-and-fire 模型中是无法做到的。文章提出了与传统 LIF 相反的模型，iLIF，在每个时间步结束后增幅而不是减少模电压，即在公式中的模电压衰减系数 k 现在是一个大于 1 的数，被称作为电压增幅系数。
然而，时域分离的方法使得完成一个神经元计算的时间翻倍，文章通过流水线的方法，在前一层的脉冲输出阶段直接将信号传输至下一层作为输入信号。在消除了时域分离带来的额外运行时间的同时，也减少了需要临时存储的内容。
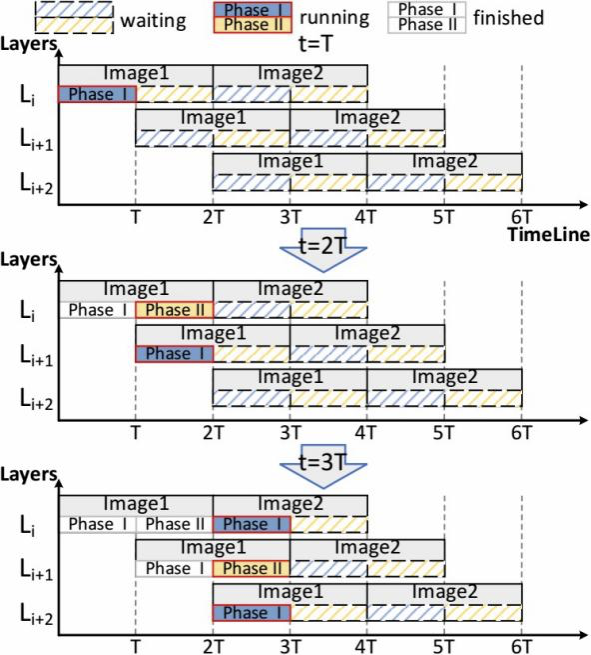
以上示意图展示了图片推理的执行示意图。核心是利用层间并行，实现不同图片的两个执行阶段重叠，降低推理时延。
参数选择方面，主要是电压增幅系数的选择。文章考虑了不同的时间步数量和增幅系数的情况下，平均的转化误差。实验表明在不同的时间步选择下，k=2 都是最优选择。
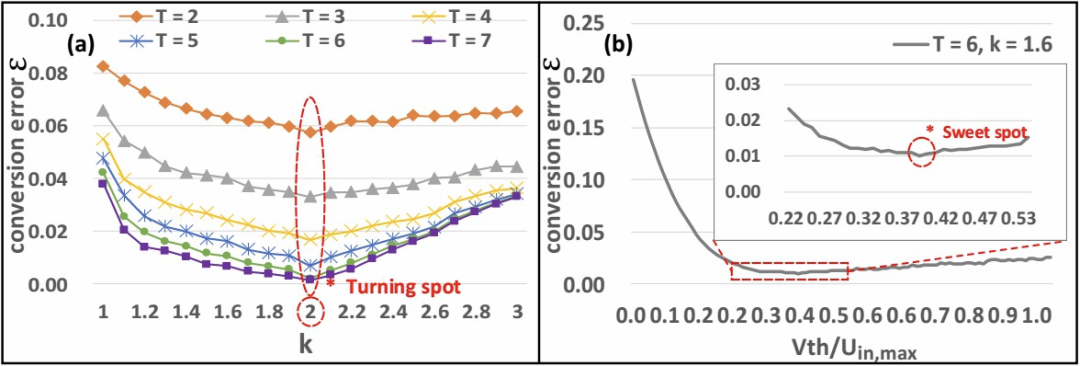
以上示意图展示了在不同参数选择下，转化误差的变化情况。K=2 时，在各个时间步下，转换误差最小，可以膜电压累积表示的信息最准确。
实验结果
文章使用 CIFAR-10/100，以及 ImageNet 数据集进行实验。实验结果表明文章提出的方法在仅需要 16 个时间步的情况下，可以达到和传统神经网络几乎一致的精度。极大节省空间存储和计算代价的情况下取得了最佳的性能，具体实验结果参见论文。部分结果如下。
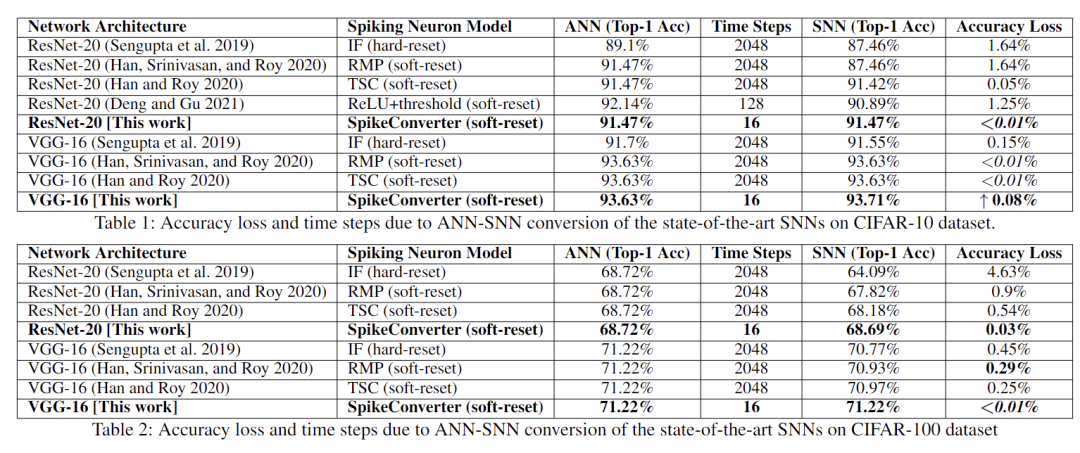
未来方向
脉冲神经网络还有较大的挖掘空间，还有许多领域 SNN 未能成功应用，可以在视频识别、机器人控制等方面继续研究。
