
一、基础
二叉树是每个节点最多有两个子树的树结构,其具有如下性质:
- 二叉树中,第 i 层最多有 2^(i-1) 个结点。
- 如果二叉树的深度为 K,那么此二叉树最多有 2K-1 个结点。
- 对任何一棵二叉树,如果其叶子结点(度为0)数为m, 度为2的结点数为n, 则m = n + 1。
二、二叉树分类
满二叉树
如果二叉树中除了叶子节点,每个节点的度都为2,则此二叉树称为满二叉树。
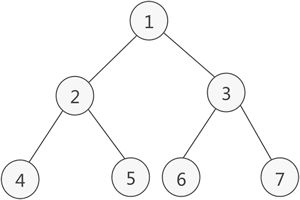
满二叉树示意图
完全二叉树
如果二叉树中除去最后一层节点为满二叉树,且最后一层的节点依次从左到右分布,则此二叉树称为完全二叉树。

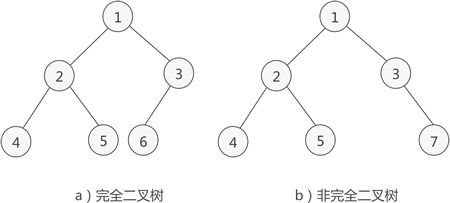
完全二叉树示意图
搜索二叉树
如果一棵树不为空,并且如果它的根节点左子树不为空,那么它左子树上面的所有节点的值都小于它的根节点的值,如果它的右子树不为空,那么它右子树任意节点的值都大于它的根节点的值,且左右子树也是二叉搜索树。
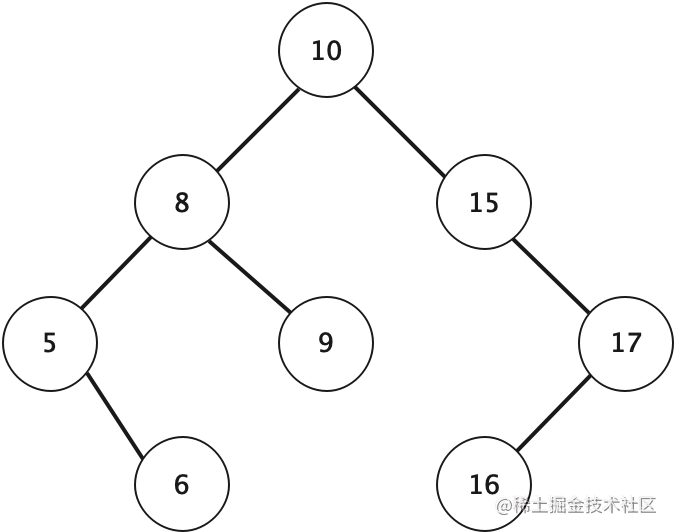
平衡二叉树
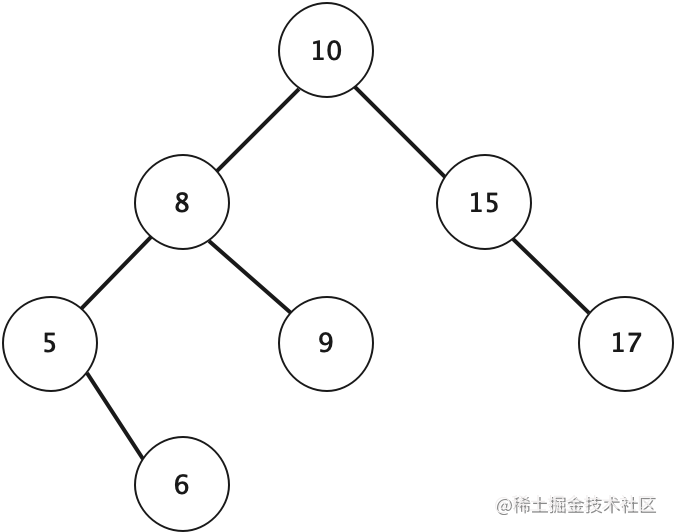
平衡二叉树又称为AVL树,是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
三、二叉树遍历
为了实现二叉树遍历,首先需要的有一颗二叉树,下面先设计一个简单的二叉树,如下所示:
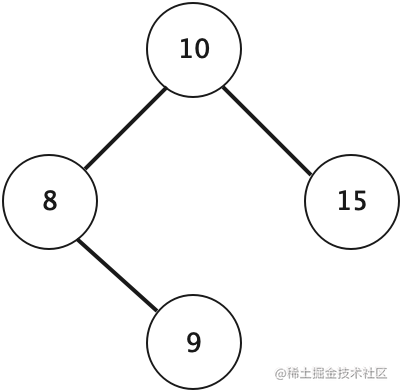
// js版本
const binaryTree = {
val: 10,
left: {
val: 8,
right: {
val: 9
}
},
right: {
val: 15
}
};
(1)先序遍历
二叉树的先序遍历是按照“根节点——左节点——右节点”的顺序遍历这颗二叉树,具体实现如下所示:
// 递归版本
function preOrderTraverse(head) {
if (head == null) {
return;
}
console.log(head.val);
preOrderTraverse(head.left);
preOrderTraverse(head.right);
}
// 对于先序遍历的非递归版,准备一个栈,然后将头压入栈中,循环弹出一个值,有右孩子的先压右孩子,再压左孩子
function preOrderTraverseUnRecur(head) {
if (head == null) {
return;
}
const stack = [];
stack.push(head);
while (stack.length > 0) {
head = stack.pop();
console.log(head.val);
if (head.right != null) {
stack.push(head.right);
}
if (head.left != null) {
stack.push(head.left);
}
}
}
(2)中序遍历
二叉树的中序遍历是按照“左节点——根节点——右节点”的顺序遍历这颗二叉树,具体实现如下所示:
// 递归版本
function inOrderTraverse(head) {
if (head == null) {
return;
}
inOrderTraverse(head.left);
console.log(head.val);
inOrderTraverse(head.right);
}
/**
* 非递归版本实现
* 准备一个栈
* 先将左节点全压入栈中
* 当前节点为空,则从栈中拿一个打印,当前节点往右跑
*/
function inOrderTraverseUnRecur(head) {
if (head == null) {
return;
}
const stack = [];
while (stack.length > 0 || head != null) {
if (head != null) {
stack.push(head);
head = head.left;
} else {
head = stack.pop();
console.log(head.val);
head = head.right;
}
}
}
(3) 后续遍历
二叉树的后序遍历是按照“左节点——右节点——根节点”的顺序遍历这颗二叉树,具体实现如下所示:
// 递归版本
function posOrderTraverse(head) {
if (head == null) {
return;
}
posOrderTraverse(head.left);
posOrderTraverse(head.right);
console.log(head.val);
}
// 对于后续遍历的非递归版,后续左-右-根,但我们可以根据根-右-左,然后将其存入一个栈中,弹出就是左-右-根
function posOrderTraverseUnRecur(head) {
if (head == null) {
return;
}
const stack = [];
const stack1 = [];
stack.push(head);
while (stack.length > 0) {
head = stack.pop();
stack1.push(head.val);
if (head.left != null) {
stack.push(head.left);
}
if (head.right != null) {
stack.push(head.right);
}
}
while (stack1.length > 0) {
console.log(stack1.pop());
}
}
(4) DFS(深度优先遍历)
深度优先遍历主要思路是从根节点开始,沿着一条路一直走到底,然后从这条路尽头的节点回退到上一个节点,再从另一条路开始走到底,不断递归重复,直到所有的顶点都遍历完。对于二叉树的深度优先就是二叉树的先序遍历。
function DFS1(head) {
if (head == null) {
return;
}
console.log(head.val);
DFS1(head.left);
DFS1(head.right);
}
// 对于二叉树的深度优先就是二叉树的先序遍历,用一个栈实现
function DFS2(head) {
if (head == null) {
return;
}
const stack = [head];
while (stack.length > 0) {
head = stack.pop();
console.log(head.val);
if (head.right != null) {
stack.push(head.right);
}
if (head.left != null) {
stack.push(head.left);
}
}
}
(5) BFS(广度优先遍历)
广度优先遍历指的是一层一层的遍历树的内容,可利用队列来实现。
function BFS(head) {
if (head == null) {
return;
}
const list = [head];
while (list.length > 0) {
head = list.shift();
console.log(head.val);
if (head.left != null) {
list.push(head.left);
}
if (head.right != null) {
list.push(head.right);
}
}
}




























