教你几个 Java 中的技巧，你会几个？-java小技巧

枯燥的编程中总得有些乐趣，今天我们不谈论那些高深的技能，教你几个在编程中的奇技淫巧，说不定在某些时候还能炫耀一番呢。

1.找到最大值和最小值

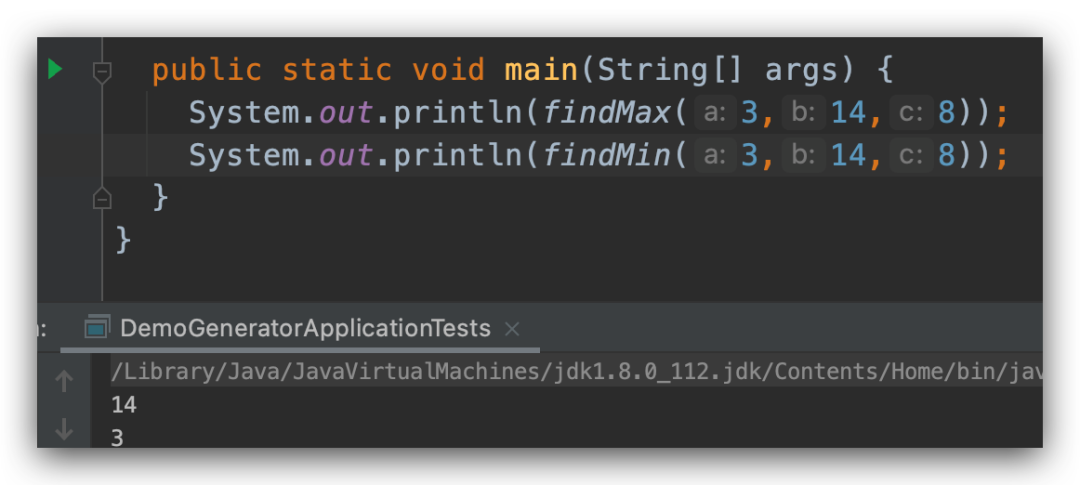
不使用 if else switch 和三元运算符，在给定的三元组中找到最大值和最小值：比如给定 3，14，8，在不使用 if else switch 和三元运算符的情况下找到最大值和最小值。

话不多说，我们先看代码：

public static int findMax(int a, int b, int c) {
    int max = a;
    boolean b1 = (max < b) && ((max = b) > 0);
    b1 = (max < c) && ((max = c) > 0);
    return max;
  }

  public static int findMin(int a, int b, int c) {
    int min = a;
    boolean b1 = (min > b) && ((min = b) > 0);
    b1 = (min > c) && ((min = c) > 0);
    return min;
  }

这里我们主要使用了&& 运算符的短路特性，短路特性是指当 && 前一个表达式为 true 的时候才会继续执行下一个表达式，当前一个表达式为 false 则不会执行下一个表达式。所以在这里只有当前一个表达式为 true 的时候，后面的赋值语句才会被执行到。

我们运行一下结果如下：

上面的这种方式入参适合正数和负数，如果当我们的入参能确定为正数的时候，我们还可以使用下面的这种方式来实现。

public static int findPositiveMax(int a, int b, int c) {
    int max = 0;
    while (a > 0 || b > 0 || c > 0) {
      a--;
      b--;
      c--;
      max++;
    }
    return max;
  }

  public static int findPositiveMin(int a, int b, int c) {
    int min = 0;
    while (a > 0 && b > 0 && c > 0) {
      a--;
      b--;
      c--;
      min++;
    }
    return min;
  }

上面的这种写法相信大家都能看懂，阿粉就不过的解释了，同样的这里也利用了&&和 || 运算的短路特性，不过要注意这种形式只能在都是正数的情况下才可以。

2.不使用临时变量交换变量

swap(x, y) 操作大家都知道，就是交互 x 和 y 的值，比如 x = 3, y = 4; 在经过 swap 操作过后，x = 4，y = 3;我们这里的问题是如何在不使用临时变量的情况下，只有一行代码来实现这个方法。

首先大家肯定知道这里我们要使用异或运算^，没错，话不多说我们看代码：

public static void swapByXor(int x, int y) {
    System.out.println(x + ":" + y);
    x = x ^ y ^ (y = x);
    System.out.println(x + ":" + y);
  }

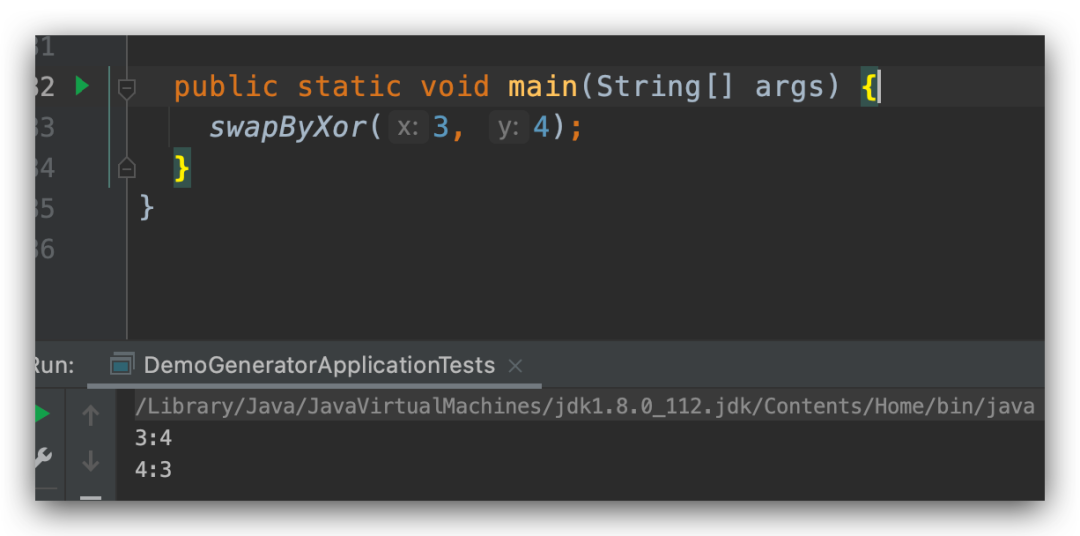
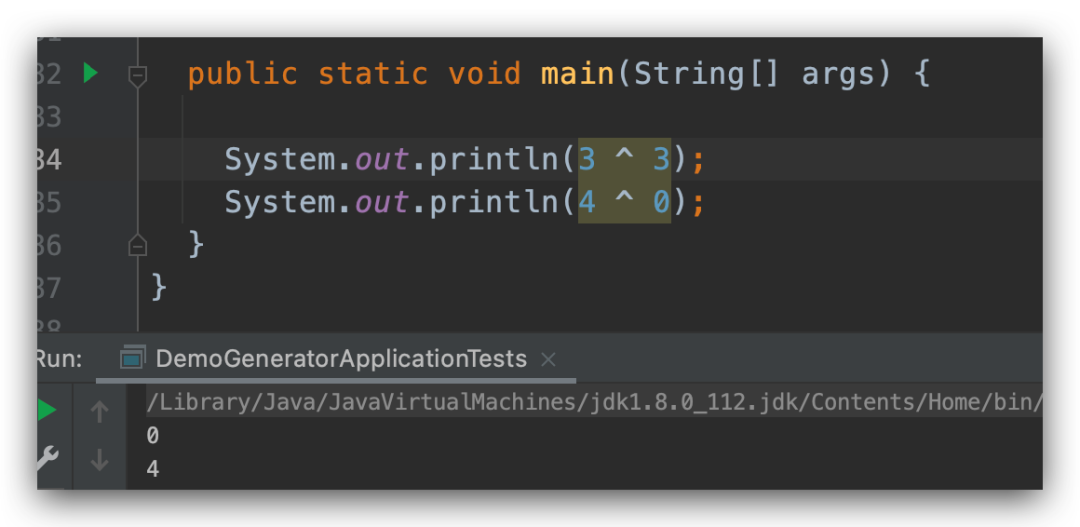
运行过后，可以看到，x 和 y 的值已经被交换了，这里我们要知道两个知识点，那就是 n ^ n = 0; n ^ 0 = n，另外a ^ b 和 b ^ a 是等价的。

当然除了上面的异或之外，我们还可以通过下面这种方法来实现。

public static void swapByAddAndSub(int x, int y) {
    System.out.println(x + ":" + y);
    x = x + y - (y = x);
    System.out.println(x + ":" + y);
  }

  public static void swapByMulAndDiv(int x, int y) {
    System.out.println(x + ":" + y);
    x = (x * y) / (y = x);
    System.out.println(x + ":" + y);
  }

这两种方式都是同样的逻辑，先求和再减去其中一个值和先求积再除以一个值，就可以得到两个替换后的值。

3.两个数相乘

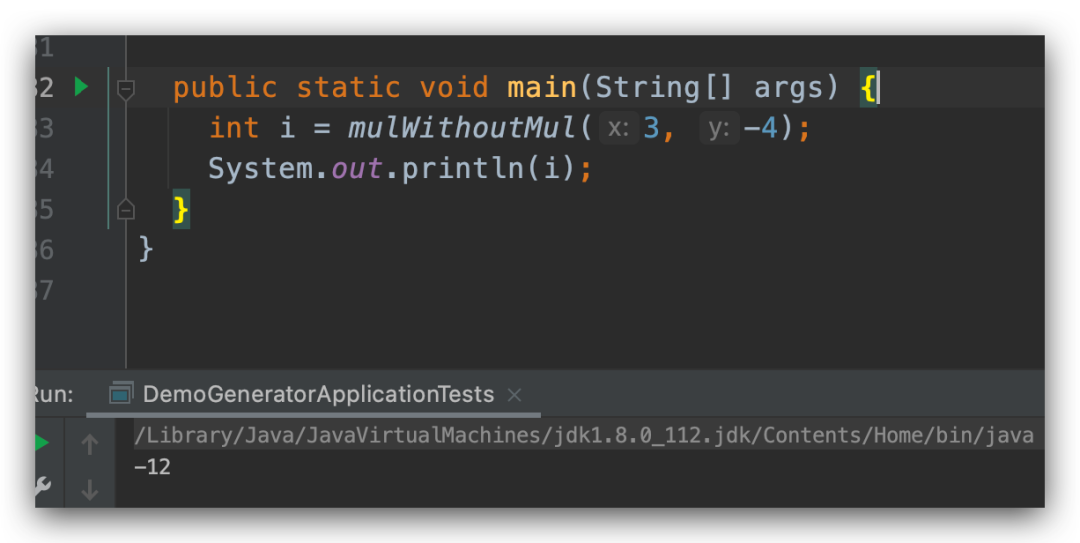
接下来我们再看一个，求两个数的积，但是不能用乘号*。在看代码之前，我们先分析一下，比如说我们要求积 3 * 5 可以将 3 * 5 看成 3 * 4 + 3，也就是 (3 * 3 + 3) + 3，看到这个可能有的小伙伴已经知道我们要怎么计算了，没错，那就是我们可以用递归。

public static int mulWithoutMul(int x, int y) {
    if (y == 0)
      return0;
    if (y > 0)
      return (x + mulWithoutMul(x, y - 1));
    return -mulWithoutMul(x, -y);
  }

通过上面的递归，我们就可以实现两个数相乘但是没有使用乘号了。

4.不使用乘号计算乘以 15

如果我们要计算一个数乘以 15 的时候，我们可以通过下面这种方式来计算，(n << 4) - n, 因 n * 15 = n * 16 - n = (n << 4) - n;同样的如果我们某些时候要计算乘以 2 或者除以 2 的时候，我们也可以换成移位操作，n * 2 = n << 1;n / 2 = n >> 1，如果是 4 的话就可以左移 2 位或者右移 2 位，即 n * 4 = n << 2;n / 4 = n >> 2;一次类推。

使用移位的方式，在某些极端的场景可以提升性能。