如何判断某网页的 URL 是否存在于包含 100 亿条数据的黑名单上-如何判断url是否可用

现在想要实现一个网页过滤系统，利用该系统可以根据网页的 URL 判断该网页是否在黑名单上，黑名单现在已经包含 100 亿个不安全网页的 URL，每个网页的 URL 最多占用 64B(字节) 大小。

请设计该系统，要求：

最简单的想法，把黑名单中所有的 URL 通过数据库或哈希表保存下来，然后遍历一遍就能判重。

But，每个 URL 有 64 B(字节)，黑名单中有 100 亿条 URL，那想要用数据库或者哈希表把这些数据全部存储起来，至少需要 640GB 的空间，显然不满足要求 2(使用的额外空间不要超过 30GB)。

事实上，这个题目有一个很明显的提示，那就是允许失误率!

类似的这种网页黑名单系统、垃圾邮件过滤系统、爬虫的网址判重系统等题目，一般都是允许一定的失误率的，但是对空间要求比较严格。

啥也别说第一个就应该想到布隆过滤器。

简单介绍下布隆过滤器的基本构造，其实就是一个 BitMap(更简单点来说其实就是一个数组)，BitMap 中每个位上的元素由若干个哈希函数进行赋值。布隆过滤器的优势在于使用很少的空间就可以将准确率做到很高的程度(但想做到完全正确是不可能的)。

哈希函数(散列函数)就不用多少了，主要有以下节点特性：

显然，返回值分布越均匀，哈希函数就越优秀。有兴趣的小伙伴可以了解哈希函数的一些经典实现，比如 MD5 和 SHA1算法，这里就不详细介绍了。

再来看布隆过滤器。假设有一个长度为 m 的 bit(位) 类型的数组(也就是 BitMap 位图，上篇文章介绍过的)，即数组中的每一个位置只占一个 bit(每一个 bit 只有 0 和 1 两种状态)：

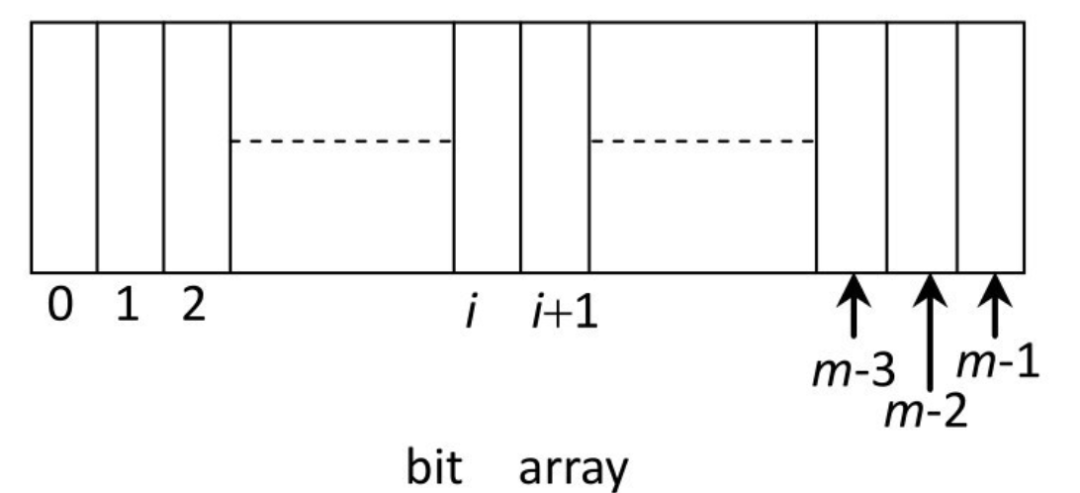
再假设一共有 k 个不同的哈希函数，它们的输出域都 >= m。

那么对同一个输入对象(假设是一个 URL，字符串)，经过 k 个哈希函数算出来的结果也是不一样的(当然也有可能相同)。对算出来的每一个结果都对 m 取余(%m)，然后在 BitMap 上把相应的位置设置为 1(涂黑)：

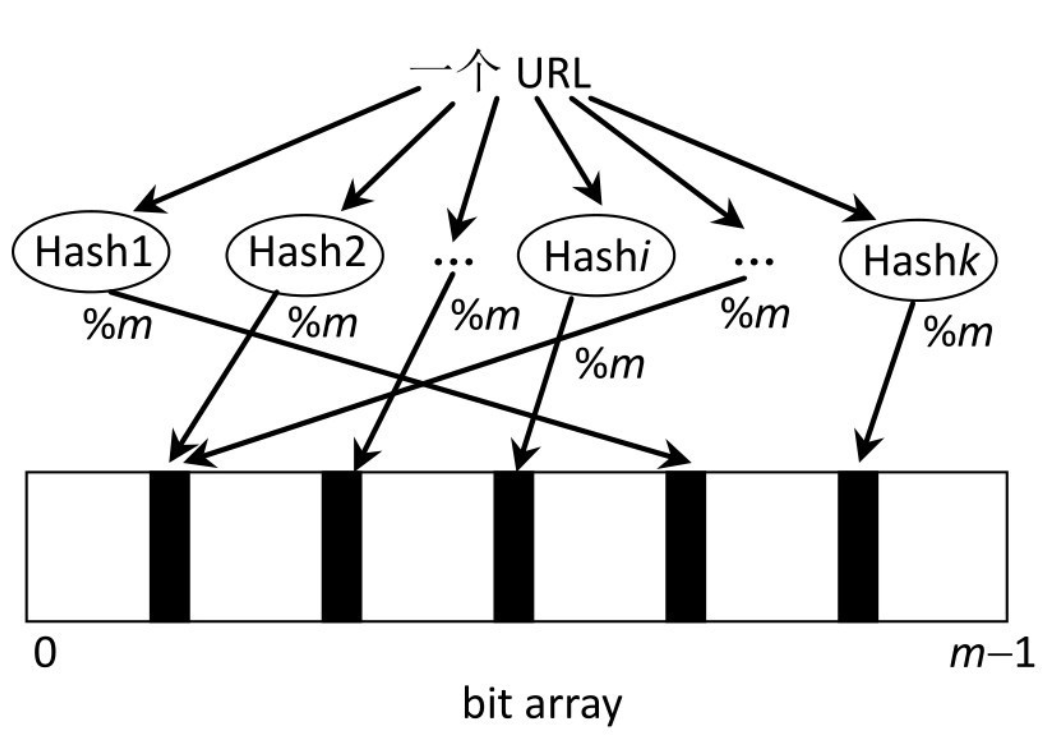
按照上述方法，我们处理所有的输入对象(黑名单中 200 亿条 URL)，每个对象都可能把 BitMap 中的一些白位置涂黑(0 的位置为 1)。

这样，存储了黑名单中 200 亿条 URL 的布隆过滤器就构造完成了。

那么假设这时又来了一个新值，如何判断这个新值之前是否已经存在呢?(如何判断某个网页的 URL 是否在黑名单上呢?)

记这个网页的 URL 为 input，想检查它是否是存在于黑名单(BitMap)中，就把 input 通过同样的 k 个哈希函数，得到 k 个值，然后继续同样地把 k 个值取余(%m)，就得到在 [0, m-1] 范围上的 k 个值，接下来在 BitMap 上看这些位置是不是都为黑：

解释具体一点，如果 input 的确是之前已经处理过的 URL，那么在生成布隆过滤器时，BitMap 中相应的 k 个位置一定已经涂黑了，所以在检查阶段，input 执行一遍相同的操作，肯定不会产生误判的。

会产生误判的是，input 明明不是之前已经处理过的输入对象，但由于哈希冲突的存在，可能就那么巧，两个不同的输入得到的 k 个哈希输出都是一样的(当然概率会非常小)，那么在检查 input 时，可能 input 对应的 k 个位置都是黑的，从而错误地认为 input 是输入对象。

所以用布隆过滤器设计的系统，总结来说就是：黑名单中存在的 URL，一定能够检查出来，黑名单中不存在的 URL，有比较小的可能性被误判。

对于这种误判，其实也有解决方案，那就是白名单，对已经发现的误报数据我们可以通过建立白名单来防止再次误报。

比如，已经发现 www.baidu.com 这个样本不在布隆过滤器(黑名单)中，但是每次计算后的结果都显示其在布隆过滤器中，那么就可以把这个样本加入白名单中，以后这个样本再次输入的时候，就不会进入布隆过滤器的逻辑进行判断了。

下面来用 Java 实现一个布隆过滤器，参考这篇文章：https://cloud.tencent.com/developer/article/1823271。

首先我们当然需要一个位数组，Java 提供了一个封装好的位数组 BitSet。

除此之外，写一个简单的布隆过滤器需要考虑的点有这些：

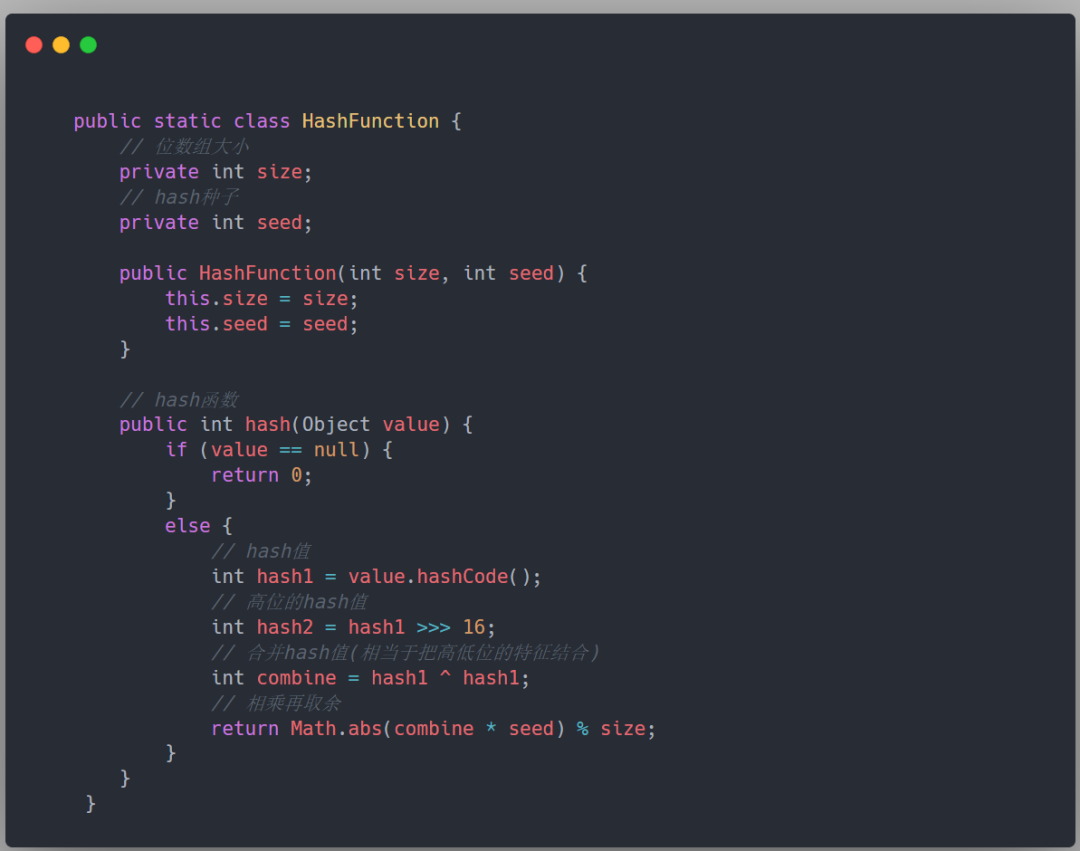
重点在下图框出来了：

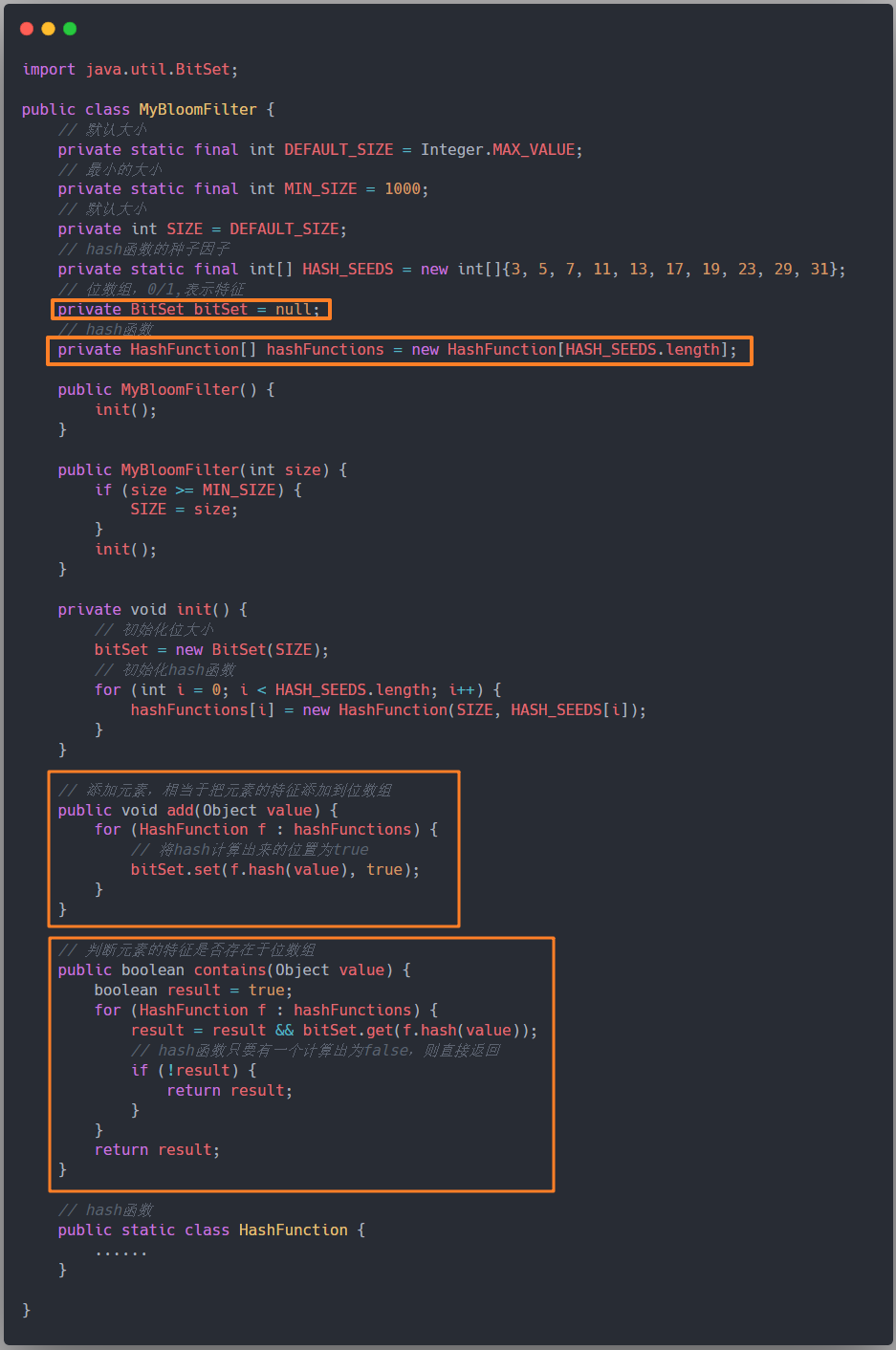
Hash 函数的实现这里就不多做研究了，给出一个比较简单的版本，主要是将 hashCode() 值的高位和低位进行异或，然后乘以预设定的种子(seed)，再对 BitMap 数组的大小进行取余数：