在计算机领域,二分查找又叫折半查找,有的地方根据其时间复杂度把它叫做对数查找,它能在对数时间内找到指定的元素,本篇文章介绍二分查找的基础和原理。
原理
二分查找算法是一种在有序数组中查找特定元素的查找算法,查找过程从数组的中间元素开始。
- 如果中间元素刚好是要查找的元素,则查找结束。
- 如果比中间元素的值小,则在数组起始到小于中间元素的那一半之间查找,而且也是从这一半儿的中间位置开始比较。
- 如果比中间元素的值大,则在数组大于中间元素到末尾元素的那一半儿之间查找,同样还是从这一半儿的中间位置开始比较。
这里有一个有序数组,元素的索引从 0 到 6,我们以它为例来说明二分查找的过程:
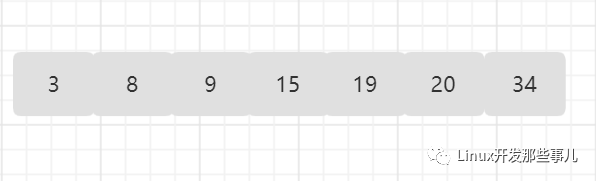
- 查找值为 15 的元素;
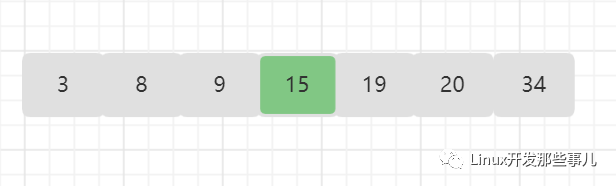
15 刚好位于数组中间的位置,所以比较一次就找到了;
- 查找值为 8 的元素;
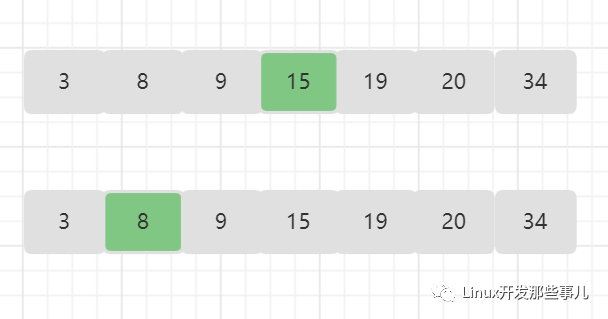
数组中间位置的元素是 15,目标值 8 小于 15,所以查找范围缩小到 15 左边的一半,也即 [ 3 , 9 ] ,这一半中间位置的元素是 8,刚好是要查找的值;
- 查找值为 34 的元素;
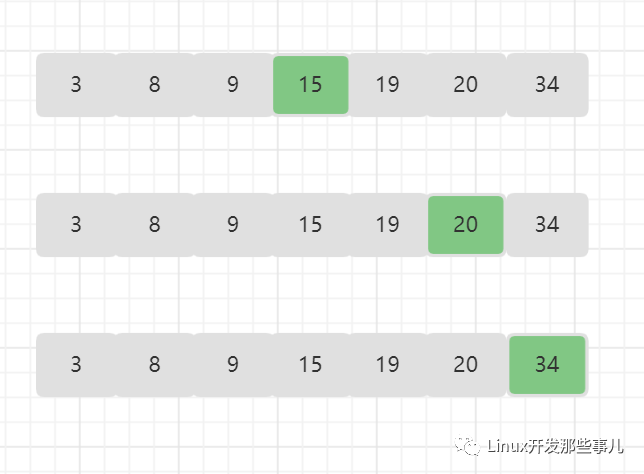
数组中间位置的元素是 15,目标值 34 大于 15,所以查找范围缩小到 15 右边的一半,也即 [ 19 , 34] ,它们的中间元素是 20,目标值 34 比 20 大,所以查找范围继续减半为 [ 34, 34 ] , 它们的中间元素是 34, 刚好是要查找的值。
基本框架
根据上述二分查找的流程,可以总结出二分查找的基本框架, 下面是伪代码:
int binary_search(vector<int> &vec, int target)
{
int left = 0; //查找范围的左边索引
int right = 0; //查找范围的右边索引
while(...) //查找结束条件
{
//数组中间元素的索引
int mid = left + (right - left) / 2;
//和目标值相等
if(target == vec[mid])
{
//处理逻辑
...
}
//目标值小于中间元素
else if(target < vec[mid])
{
//处理逻辑
left = ...
}
//目标值大于中间元素
else
{
//处理逻辑
right = ...
}
}
//返回目标值在索引中的位置,如果找不到,返回 -1
return ...
}
伪代码中的 ... 的地方是容易出现细节问题的地方, 我们自己编写或者看别人代码的时候,注意下这些地方。
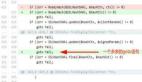
需要注意一点,计算查找范围的中间位置的索引的方法 mid = (left + right) / 2, 当数组非常大的时候, left + right 可能会超过整形最大值,所以需要修改成 mid = left + (right - left) / 2 或者 mid = left + (right - left) >> 1, 以避免溢出风险。
实现
二分查找的实现方式有多种,这里只选取前面基本框架中的方式来介绍,常见的二分查找场景有:查找一个指定的数、查找数组中第一个和目标值相等的元素,查找数组中最后一个和目标值相等的元素。
下面的算法实现代码是用 C++ 语言实现的,vector vec 表示一个整形的数组, 数组名是 vec ,类似于 Java 中的 int[] nums, 如果是 C语言的话,可以用 int *nums 和 int len 来表示也是一样的,大家可以自行用熟悉的编程语言实现。
1. 查找和目标值相等的元素
这是最基础的二分查找,只要找到了和目标值相等的元素,返回其索引,否则返回 -1,表示没找到和目标值相等元素的索引:
int binary_search(vector<int> &vec, int target)
{
int ilen = (int)vec.size();
if(ilen <= 0) return -1;
int left = 0;
int right = ilen - 1;
while (left <= right)
{
int mid = left + (right - left) / 2;
//找到了,直接返回
if (target == vec[mid]) return mid;
if(target < vec[mid]) right = mid -1;
else left = mid + 1;
}
return -1;
}
需要注意几点:
- 为什么 while 的循环条件是 <=;
因为 right = ilen - 1 , 也就最后一个元素的索引, 当 left 等于 right 的时候, 表示 到达查找范围右边的边界。
此时 mid = left = right, 当 mid 索引处的元素和目标值相等时, 返回索引 mid。
如果不相等, 要么 left = mid + 1 要么 right = mid -1 ,不管执行哪个逻辑,结果都是 left > right, 接着退出 while 循环。
- 为什么 left = mid + 1 或者 right = mid - 1;
根据前面的介绍可知,二分查找的范围是 [left, right], 当我们发现查找的目标值不等于 mid 索引元素的值时, 下一次查找的范围是 [left, mid - 1] 或者 [mid + 1, right], 因为 mid 处的元素已经比较过了,需要从查找范围中排除。
2. 第一个和目标值相等的元素
上面的二分查找有一个局限性,比如一个有序数组 {-1,-1,-1,-1,2,3}, target 的值为 -1, 此时算法返回的索引是 2, 结果是没错,但如果我想得到第一个和 target 相等元素的索引,也即 0 或者最后一个和 target 相等元素的索引, 也即 3 时, 此算法是没办法处理的, 下面就来说明这两种二分查找算法。
int binary_search_firstequal(vector<int> &vec, int target)
{
int ilen = (int)vec.size();
if(ilen <= 0) return -1;
int left = 0;
int right = ilen - 1;
while (left <= right)
{
int mid = left + (right - left) / 2;
//找到了目标,继续向左查找目标
if (target == vec[mid]) right = mid - 1;
else if(target < vec[mid]) right = mid -1;
else left = mid + 1;
}
if(left < ilen && vec[left] == target) return left;
return -1;
}
当条件 target == vec[mid] 以及 target < vec[mid] 成立时,都执行 right = mid - 1的逻辑, 这里把它们分开是为了便于大家理解,熟练以后,两个条件合并成一个。
- 为什么 target == vec[mid] 时 right = mid - 1;
当 mid 索引处的值和目标值相等时, 我们需要在 mid 的左边继续查找 , 看是否存在和目标值相同的元素, 所以查找范围变成了 [ left, mid - 1] , 故需要执行 right = mid - 1的逻辑。
- 为什么最后返回时要加上 left < ilen && vec[left] == target 的条件;
while 循环退出条件是 left = right + 1, 当 target 的值比数组中元素的值都大的时候, left 索引的值会超过数组的最大索引, 所以需要进行索引边界校验,也即 left < ilen。
当 target 的值处于数组最大元素和最小元素之间且数组中不存在和target 值相等的元素时, 此时无法找到一个索引,使得元素的值和 target 相等, 所以,还需要进行 vec[left] == target 的逻辑判断。
- 为什么返回 left 而不是 right;
也可以返回 right, 把最后的判断改成 if ( right + 1 < ilen && vec[right + 1] == target) return right+1; 即可。
当找到数组中第一个和目标值相等的元素时, 执行了 right = mid - 1, 然后就退出了 while 循环, 而实际的索引值应该是 mid , 也就是 right + 1。
3. 最后一个和目标值相等的元素
和 查找第一个和目标值相等的元素 算法稍有不同, 此二分查找算法找到和目标值相等元素之后,查找范围需要往右移动,继续找下一个和目标值相等的元素。
int binary_search_lastequal(vector<int> &vec, int target)
{
int ilen = (int)vec.size();
if(ilen <= 0) return -1;
int left = 0;
int right = ilen - 1;
while (left <= right)
{
int mid = left + (right - left) / 2;
//找到了目标,继续向右查找目标
if (target == vec[mid]) left = mid + 1;
else if(target < vec[mid]) right = mid -1;
else left = mid + 1;
}
if(left - 1 < ilen && vec[left - 1] == target) return left - 1;
return -1;
}
有几个细节需要注意下:
- 为什么 target == vec[mid] 时 left = mid + 1;
当 mid 索引处的值和目标值相等时, 我们需要在 mid 的右边继续查找 , 看是否存在和目标值相同的元素, 所以查找范围变成了 [ mid + 1, right] , 故需要执行 left = mid + 1的逻辑。
- 为什么最后返回时要加上 left - 1 < ilen && vec[left - 1] == target 的条件;
当 target 大于或者等于数组中元素的时候, 查找范围左边的边界会右移,即 left = mid + 1, 即使找到了最后一个和目标值相等的元素时,left 还是会向右移动一个位置,所以,实际的位置是 left - 1 而不是 left。
当 target 的值处于数组最大元素和最小元素之间且数组中不存在和target 值相等的元素时, 此时无法找到一个索引,使得元素的值和 target 相等, 所以,还需要进行 vec[left-1] == target 的逻辑判断。
小结
本文介绍了二分查找算法的原理以及常见的实现方式,网上还有很多其他的实现方式,比如:递归的方式、左闭右开的查找范围的方式,它们的原理都是一样的,只是在细节上有差别,只要弄清楚了本文介绍的所有细节处理的原因,其他版本的二分查找是很容易就能弄明白的。