图解算法基础-快速排序，附 Go 代码实现-快速排序算法代码

很多面试题的解答都是以排序为基础的，如果我们写出一个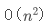的算法，大概率要被挂，今天写个快排的基础文章，后面看情况再把归并和堆排序写一写，至于选择排序、冒泡排序这种时间复杂度高的就不写了，有兴趣的可以找书自己看一下。

文中算法的实现是用 Go 写了一个比较简单的快速排序，方便大家理解(旁边画外音：其实是他好几年没面试了，太厉害的他也写不出来)。

关于更优秀的代码实现，可以在评论区里发出来一起学习，相信咱们读者里一定是卧虎藏龙，有不少算法大拿。

快速排序的思想

快速排序算法首先会在序列中随机选择一个基准值(pivot)，然后将除了基准值之外的数分为 "比基准值小的数" 和 "比基准值大的数" 这两个类别，再将其排列成以下形式。

【比基准值小的数】 基准值 【比基准值大的数】

接着，继续对两个序列 "【】"中的数据进行排序之后，整体的排序便完成了。对基准值左右两侧的序列排序时，同样也会使用快速排序。

快速排序是一种"分治法"，将原本的问题分解成两个子问题—— 比基准值小的数和比基准值大的数，然后再分别解决这两个子问题。解决子问题的时候会再次使用快速排序，只有在子问题里只剩下一个数字的时候，排序才算完成。

快排的过程

下面我们用示意图更好地理解一下快速排序对一个序列进行排序的过程。

图例出自—《我的第一本算法书》。

假定有如下待排序序列：

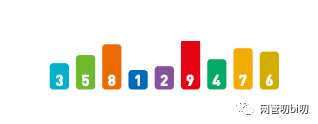
待排序序列

首先在序列中随机选择一个基准值，这里选择了 4。

选择基准值 pivot

将其他数字和基准值进行比较，小于基准值的往左移，大于基准值的往右移。

首先比较第一个元素 3 和基准值4，因为 3 < 4, 所以将 3放在基准值的左边。

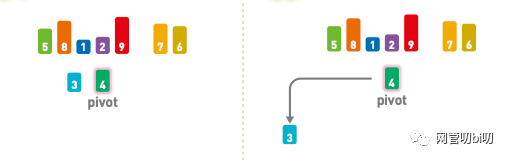
首先比较 3 和基准值4，因为 3 < 4, 所以将 3放在基准值的左边

接下来，比较 5 和基准值，因为 5 > 4，所以将 5 放在基准值的右边。

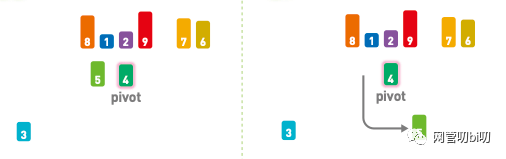
5 > 4，将5放在基准值右边

对整个序列进行同样操作后，所有小于基准值的数字全都放到了基准值的左边，大于的则全都放在了右边。

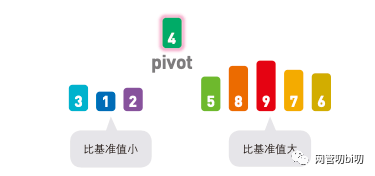
一轮排序完成后的结果

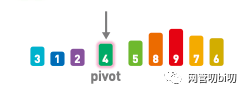
把基准值放入序列

现在排序就分成了两个子问题，分别再对基准值左边和右边的数据进行排序。

分解成了两个子问题

两边的排序操作也和前面的一样，也是使用快排算法，选取基准值，把小于的数字放左边大于的放右边。

对子序列使用快速排序

子问题有可能会再分解成子问题，直到子问题里只剩下一个数字，再也无法分解出子问题的时候，整个序列的排序才算完成。

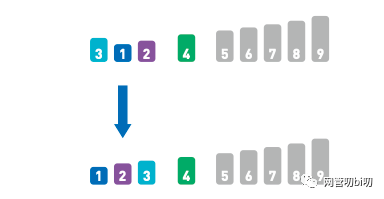
排序完成

因为快速排序算法在对序列进行排序的过程中会再次使用该算法，所以快速排序算法在实现时需要使用"递归”来实现。

快速排序的Go代码实现

下面上一个用 Go 版本的快速排序算法的简单实现：

func quickSort(sequence []int, low int, high int) {
 if high <= low {
  return
 }
 j := partition(sequence, low, high)
 quickSort(sequence, low, j-1)
 quickSort(sequence, j+1, high)
}

// 进行快速排序中的一轮排序
func partition(sequence []int, low int, high int) int {
 i, j := low+1, high
 for {
  // 把头元素作为基准值 pivot
  for sequence[i] < sequence[low] {
   // i 坐标从前往后访问序列，如果位置上的值大于基准值，停下来。
   // 准备和 j 坐标访问到的小于基准值的值交换位置
   i++
   if i >= high {
    break
   }
  }
  for sequence[j] > sequence[low] {
   // j 坐标从后往前访问序列，如果位置上的值小于基准值，停下来。
   // 和 i 坐标指向的大于基准值的值交换位置
   j--
   if j <= low {
    break
   }
  }
  if i >= j {
   break
  }
  sequence[i], sequence[j] = sequence[j], sequence[i]
 }
 sequence[low], sequence[j] = sequence[j], sequence[low]

 return j
}

每一轮快速排序都会经历下面这几个步骤：

设置两个变量i、j，排序开始的时候：i=0，j=待排序序列长度 - 1。
以第一个数组元素作为基准值 pivot(也可以是最后一个元素，或者是随机的一个元素)。
i 坐标从开始向后访问序列里的元素，即 i++，找到第一个大于 pivot 的位置，和 j 坐标访问到的小于基准值的值交换位置。
j 坐标从末尾向前搜索，即j--，找到第一个小于 pivot 的位置，将i，j坐标上的值进行互换。
重复第3、4步，直到i=j，然后将 pivot 和 j 坐标上的值互换，完成一轮排序，小于 pivot 的值都放在了它的左边，大于的则放到了右边。

重复进行上面的过程，直到排序完成。最后我们可以生成一个随机数序列对上面的快速排序函数进行测试：

func main() {
 rand.Seed(time.Now().Unix())
 sequence := rand.Perm(34)
 fmt.Printf("sequence before sort: %v", sequence)
 quickSort(sequence, 0, len(sequence) - 1)
 fmt.Printf("sequence after sort: %v", sequence)
}

快速排序的时间复杂度

分割子序列时需要选择基准值，如果每次选择的基准值都能使得两个子序列的长度为原本的一半，那么快速排序的运行时间和归并排序的一样，都为 O(nlogn)。将序列对半分割 log2n 次之后，子序列里便只剩下一个数据，这时子序列的排序也就完成了。

因此，如果像下图这样一行行地展现根据基准值分割序列的过程，那么总共会有 log2n 行。

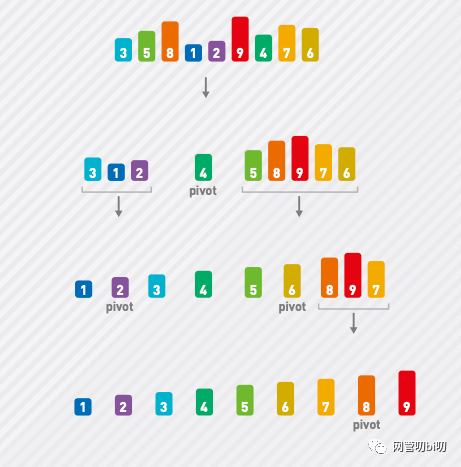
快排分解序列的次数

每行中每个数字都需要和基准值比较大小，因此每行所需的运行时间为 O(n)。由此可知，整体的时间复杂度为 O(nlogn)。

如果运气不好，每次都选择最小值作为基准值，那么每次都需要把其他数据移到基准值的右边，递归执行 n 行，运行时间也就成了。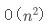

所以真正应用的时候基准值的选取也比较讲究，比如以中位数做基准值：本轮排序序列的第一个、最后一个、中间位置三个数的中位数作为基准值进行排序。