虽然在高中数学里,大家都接触过虚数这个概念,但它看起来总是那么反直觉:虚数这个名词是 17 世纪数学家笛卡尔提出的,因为当时的观念认为这不是真实存在的数字,其性质被定义为:
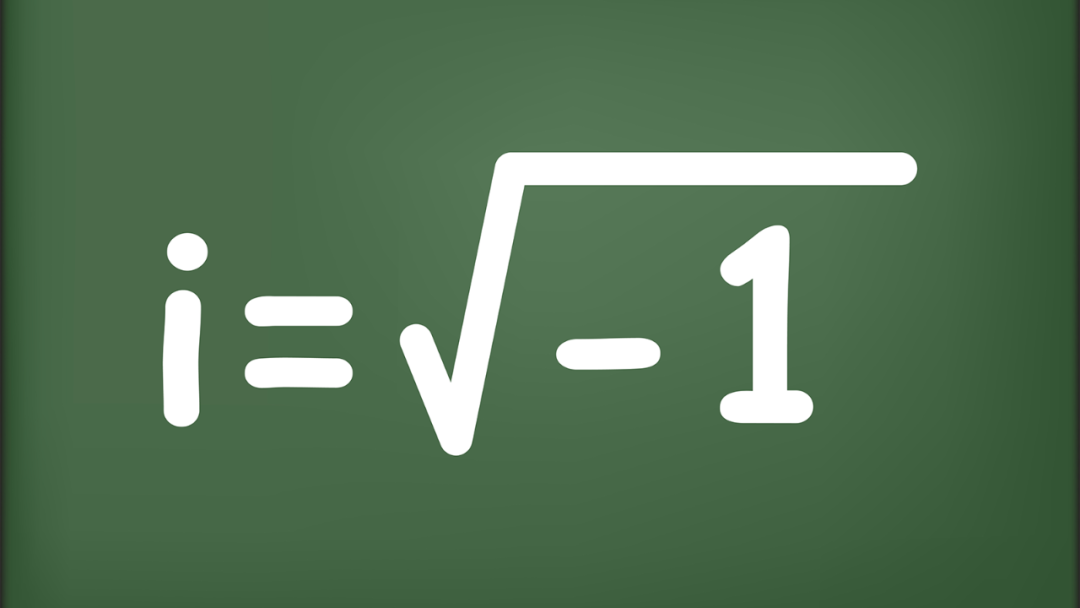
但是现如今,为了从根本上描述物质,虚数被证明是必不可少的。它们似乎融入了量子力学的结构,后者是描述分子、原子和亚原子粒子领域的基础理论。最近的两项新实验表明,遵循量子物理学规则的理论需要虚数来描述现实世界。
虚数由负数的平方根产生。它们经常作为数学工具出现在方程式中,以使计算更容易。但是我们可以实际测量的,关于世界的一切都是用实数来描述的,我们也习惯于正常的、非虚的数字。
在量子物理的范畴中其实也是如此。尽管虚数出现在理论的内部运作中,但所有可能的测量都会产生实数。
虚数 i 是薛定谔方程必不可少的常数,由此观之,量子力学必须包含虚数。量子理论对复数(虚数和实数之和)的突出使用令其创始人,包括物理学家艾尔温 · 薛定谔(Erwin Schrödinger)感到不安。「从量子理论的早期开始,复数更多地被视为一种数学便利,而不是基本的构建模块,」南方科技大学的物理学家范靖云说道。
部分物理学家试图仅使用实数来构建量子理论,而使用称为「实数量子力学」的版本来避免使用虚数。但是如果没有对这些理论进行实验测试,我们无法得知虚数在量子物理学中是否真的必要,或者只是一种有用的计算工具。
一种称为贝尔测量(Bell test)的实验解决了一个不同的量子难题,证明量子力学确实需要粒子之间的奇怪量子联系,也就是量子纠缠。
要了解标准量子理论和类似实数理论之间的区别,你可以思考限制在两个不同位置上的电子。在量子理论中,电子可以处于两个位置的「叠加」中——既不在这个位置,也不是在另一个位置,被观测到在哪只看概率。这种叠加被表示为包含两个维度的抽象空间中的一个点。
但这不是普通的空间,也不容易想象。抽象空间中的每个维度都通过一个复数与现实世界中的一个位置相关联,该复数可用于计算在该位置找到电子的概率。随着电子的状态随时间变化,该点在抽象空间中移动。

具有两个真实维度的类比空间不足以捕捉该电子可以表现出的所有现象,因为它无法编码两个位置的所有可能叠加。然而,具有四个真实维度的空间能够完整指出电子行为的全部范围。这个事实可以概括为:任何单个量子系统的量子物理学都可以在一个真实空间中完全表示,该真实空间的维度数恰好是其抽象空间的两倍。
维也纳量子光学和信息研究所的理论物理学家 Miguel Navascués 表示:「我们已开始思考这种实验是否也能反驳实数量子力学。」他和来自奥地利、西班牙和瑞士等国家的科学家在 12 月 15 日发表于《自然》杂志的论文《Quantum theory based on real numbers can be experimentally falsified》中制定了一项实验计划。该论文的一作是量子信息科学的理论物理学家 Marc-Olivier Renou。
论文链接:https://www.nature.com/articles/s41586-021-04160-4
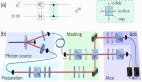
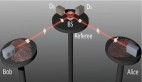
在实验计划中,研究人员将从两个不同的来源发送成对的纠缠粒子给三个不同的人,根据传统的物理术语命名为 Alice、Bob 和 Charlie。Alice 接收到一个粒子,并且可以使用她选择的各种设置对其进行测量,Charlie 也这样做。Bob 接收到两个粒子并执行一种特殊类型的测量来纠缠 Alice 和 Charlie 接收到的粒子。
没有虚数的实数量子理论将预测与标准量子物理学不同的结果,从而使实验能够区分哪个是正确的。
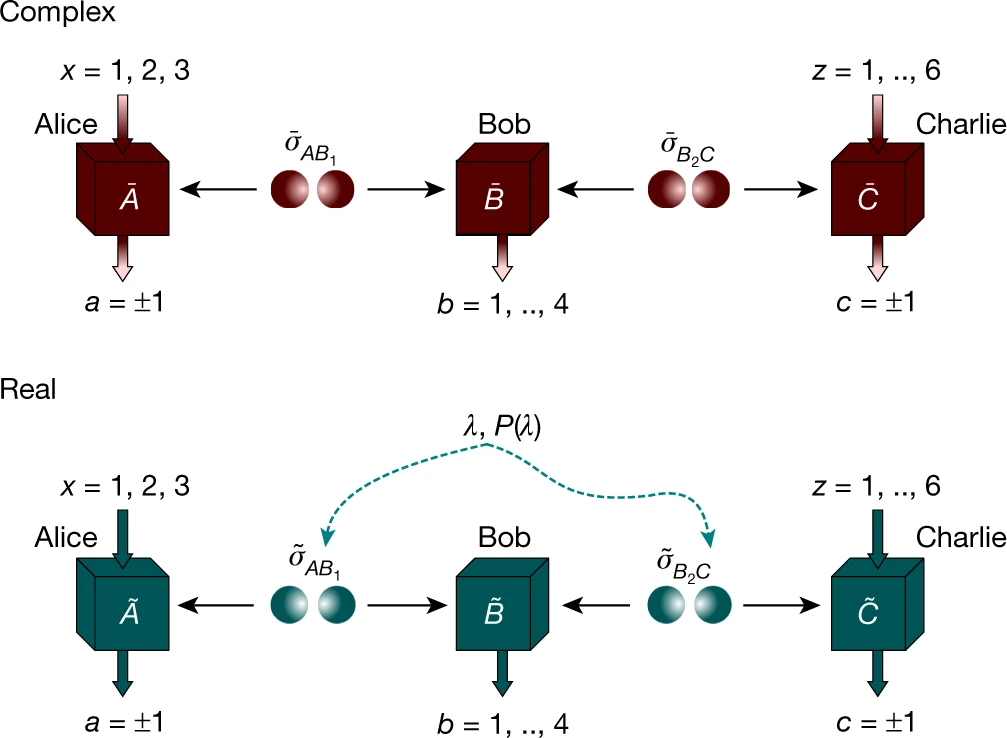
分离实数量子理论和复数量子理论的网络场景。
范靖云及其同事使用光子和光粒子进行了这样的实验,他们在 1 月 24 日发表在物理学顶级期刊《物理评论快报》(Physical Review Letters,PRL)上的论文《Testing Real Quantum Theory in an Optical Quantum Network》中进行了报告。通过将 Alice、Charlie 和 Bob 的结果以多种度量方式进行比较,范靖云、Navascués 及其同事表明这些数据只能用包含复数的量子理论来描述。

论文链接:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.128.040402
与此同时,中科大潘建伟团队基于相同的概念,使用由超导体制成的量子计算机进行了一项实验。这项研究也发现量子物理学需要复数,论文《Ruling Out Real-Valued Standard Formalism of Quantum Theory》也在近日的 PRL 上发表。

论文链接:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.128.040403
潘建伟、陆朝阳、朱晓波等和西班牙塞维利亚大学 Cabello 教授合作,利用超高精度超导量子线路实现确定性纠缠交换,以超过 43 个标准差的实验精度证明了实数无法完整描述标准量子力学,确立了复数的客观实在性。陈明城、王粲和刘丰铭是该论文的共同一作。
中科大在新闻稿中介绍道:随着量子力学理论的发展,复数逐渐表现出某种直觉上的不可排除性。理论上,作为量子力学基石的薛定谔方程和海森堡对易关系其本身就是依赖于复数写出的。而在实验中,人们直接测量到了波函数的实部与虚部。这说明复数可能不是一个主观引入的计算符号,而是可以实验检测的物理实在。
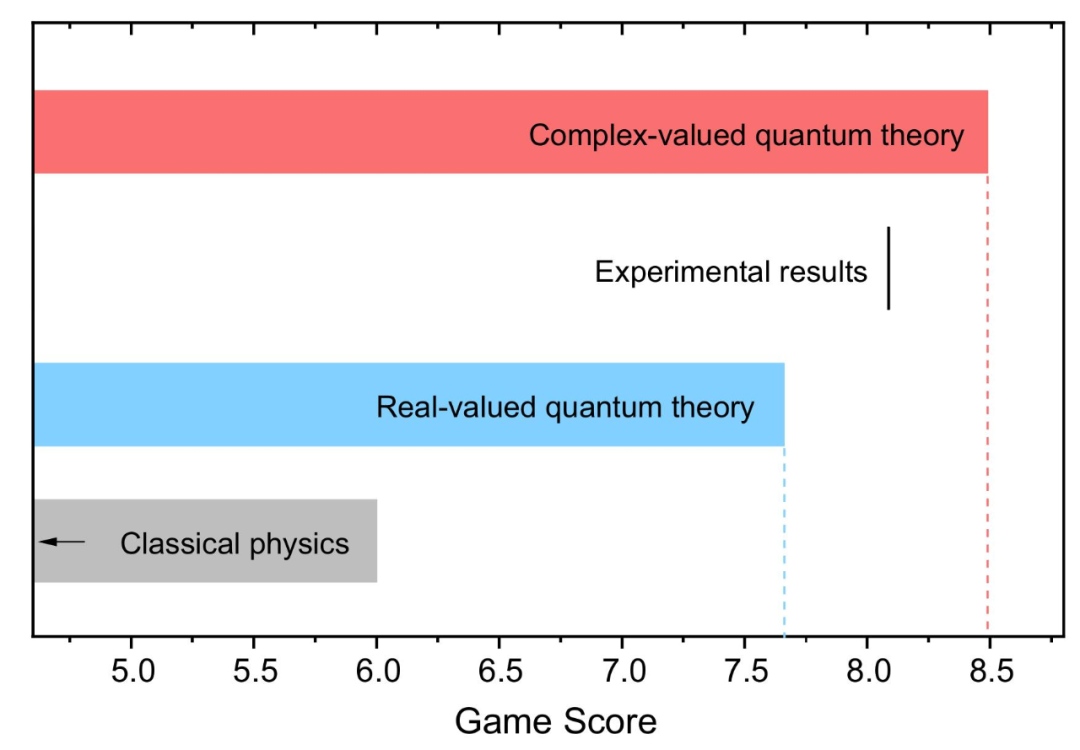
在理论框架下,实数形式的界限为 7.66,而实验测试结果为 8.09,超过判据 43 个标准差。实验结论支持量子物理需要使用复数。
中科大表示,该实验证明了实数无法完整描述标准量子力学,确立了复数的客观实在性。该论文的作者之一、中国科学技术大学的量子物理学家陆朝阳说:「我们很好奇为什么复数是必要的,并且在量子力学中发挥着重要作用。」
在 Navascués 等人的实验方案提出不久后,潘建伟等人使用超导量子电路,范靖云等人使用线性光学,分别验证了理论。但并未参与这项研究的加州劳伦斯伯克利国家实验室的理论物理学家 Jerry Finkelstein 指出:结果并未排除所有避开虚数的理论。该研究只排除了某些基于实数的理论,即那些仍然遵循量子力学惯例的理论。
通过使用打破标准量子规则的理论,仍然可以在没有虚数的情况下解释实验结果。然而 Jerry Finkelstein 说:「虽然这些理论遇到一些概念问题时会变得『丑陋』,但如果你愿意忍受『丑陋』,那么你就可以拥有一套实数量子理论。」
尽管存在质疑,但许多物理学家一致认为:「复数对于量子理论是必要的」这一新发现令人信服。
诚如美国国家标准技术研究所的物理学家 Krister Shalm 所说:「当你问量子力学『为什么会这样』时,这就已经很有趣了。而询问『量子理论是否可以更简单』,或者『它是否包含任何不必要的东西』这些都是更加有趣和发人深省的问题。」