我现在有点明白了,在面试过程中面试官有时会让我们手写代码,其实主要是考验大家的基本功,更是通过大众都熟悉的领域来考核大家的体系化思维与应对思路。
前文前文学习了基础数据结构:链表(单链表),接下来我将从leetcode中挑选几道挺有意思的算法题,与大家一起来学习。
链表中如果与相对位置有关的,基本通过引入双指针(快慢指针)即可实现一次遍历就求解。
1、检测一个单链表中是否存在环
题目:如果给你一个指定的单链表,请判断是否存在环。
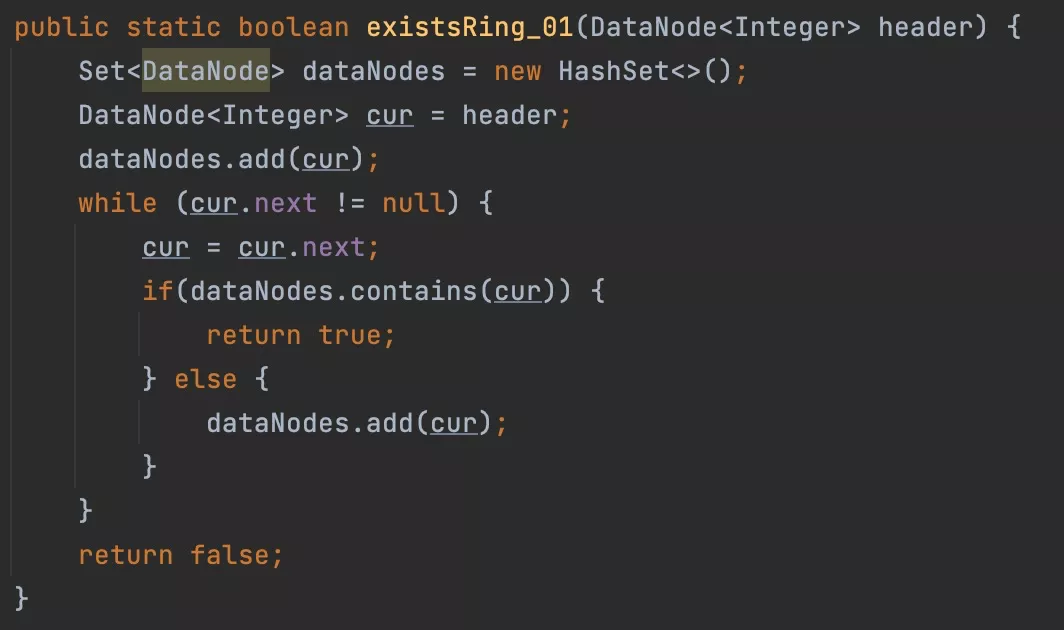
作为一个算法小白来说,看到这个题目,不假思索后想到的思路一定是:引入一个HashSet,然后从头开始遍历单链表,将每一个元素存储到HashSet中,在遍历过程中,如果该元素在节点在HashSet中存在,则表示存储环。
温馨提示:本文的链表使用上文笔者手写的链表。
代码实现如下:
在算法领域通常有两个维度来评估一款算法的优劣:时间复杂度、空间复杂度。
- 时间复杂度:O(N),因为需要遍历整个链表,随着链表数据的增长,遍历的次数就更多。
- 空间复杂度:O(N),因为这里额外申请来一个空间用来存储遍历过的节点。
进阶:能否对上述算法进行优化,将空间复杂度优化到O(1)。
在业界有一个经典的算法,龟兔赛跑算法,主要用于检测链表中是否存在环,通常可以解决如下问题:
- 检测链表中是否存在环
- 如果存在环,计算出环的入口节点
- 如果存在环,计算出环的长度
从网上获取“龟兔赛跑”的具体描述:
龟兔赛跑算法的理论一:引入两个快慢两个指针,两个指针同时从链表的头节点开始遍历,快指针每次移动2,慢指针每次移动1步,如果链表存储环,快指针最终会追上慢指针,即两个指针会重合;
接下来我们可以根据这个规则,写出示例代码如下:
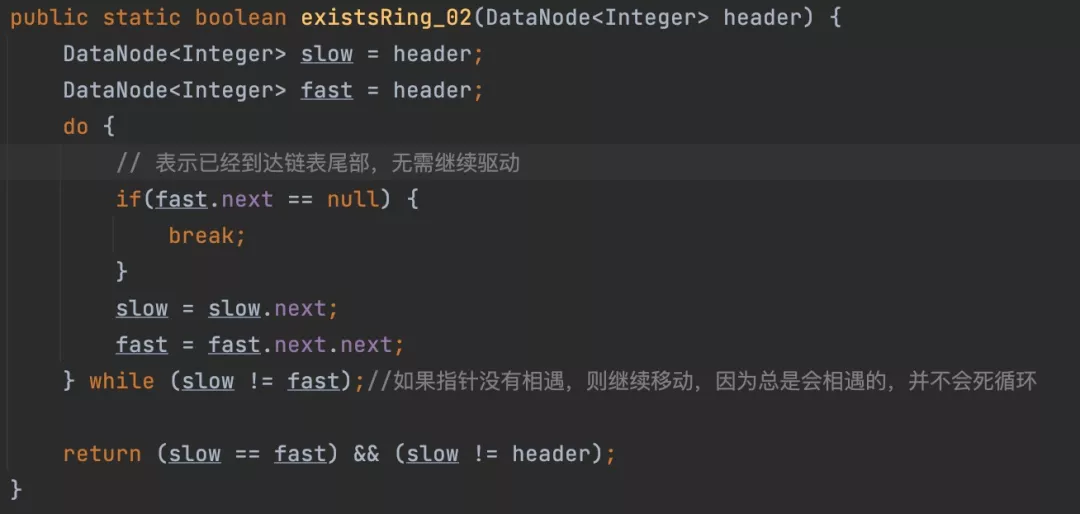
是不是非常优雅,只需要引入两个指针。
龟兔赛跑算法的理论二:快慢指针在第一次相遇后,如果要求环的入口,方法为:将slow指针移动到队列头部,然后快慢指针第一次相遇的点,即为环的入口节点。
2、删除链表中倒数第n个节点
在没有了解到“龟兔赛跑算法”之前,要删除倒数第n个节点,大家肯定会先遍历一次链表,得出链表的总长度用len表示,然后再次遍历,第二次遍历只需遍历的次数为(len-n)个节点即可。
但我们学习了龟兔赛跑算法之后,我相信读者朋友们一定也能够想到,引入两个指针,可以只需要遍历一次。
具体的解法如下:

引入两个指针,初始状态都执行Header节点,然后先让一个指针移动n次,然后两个指针同时移动,知道第一个指针到达链表的尾部,此时第二个指针就是倒数第n个节点,沿着上图,当first移动到队尾的状态图如下:
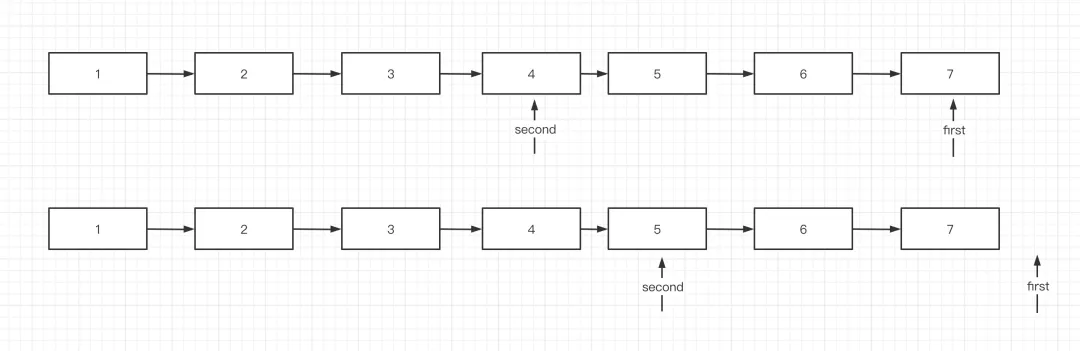
与具体写代码有关,最终如上图所示,由于是删除倒数第n个节点,并且是单链表,故通常需要先找到要删除节点的前驱节点,从这方面考虑,上述结束条件选用第一种比较合适,接下来是根据上述思路的代码实现:
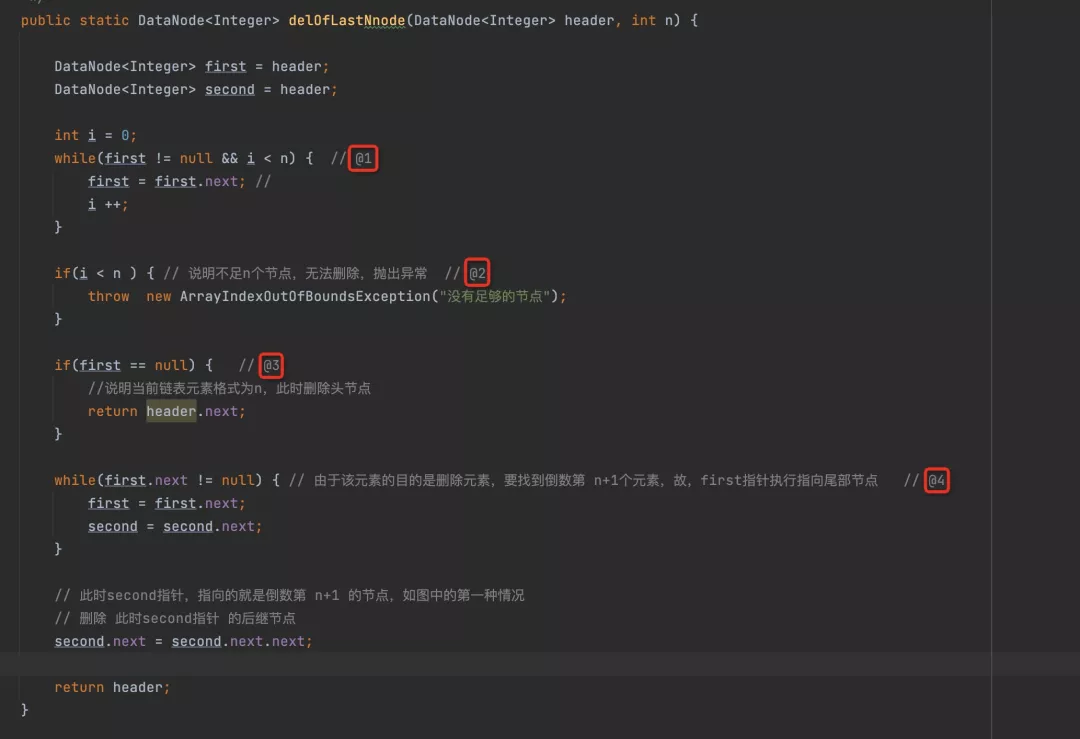
代码解读如下:
代码@1:只要当前节点不为空,就可以继续向后驱动,主要是为了保证,在刚好拥有n个节点的情况下,能驱动n次,也方便理解,例如现在有一个三个节点的链表,要删除倒数第三个,其运行轨迹如下图所示:
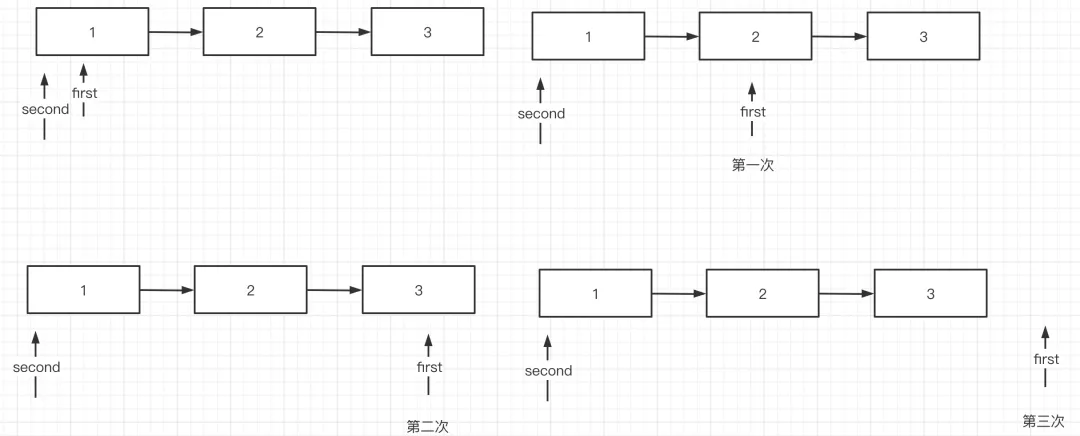
代码@2:如果i小于n,说明没有遍历n次,缺少元素,直接抛出数组越界异常。
代码@3:说明刚好遍历了n次,正如上图所示,则直接删除头节点。
代码@4:接下来将同步推进first,second指针,由于单链表删除节点,需要知道被删除节点的前驱节点,故first指针指向尾节点(node.next == null,表示到达尾部),如下图所示:

代码的解读就到这里了,不得不佩服双指针的强大之处。
3、求链表的中间节点经过上面两道题的讲解与训练,我相信读者朋友们看到这种在链表领域与位置相关的题目,终极杀器:双指针。
解题方法:中间位置,那我们可以引入快慢两个指针,快指针是慢指针的2倍速率,这样当快指针到达链表尾部,慢指针就正好走在链表的中间件位置。