大家都知道函数调用是通过栈来实现的,而且知道在栈中存放着该函数的局部变量。但是对于栈的实现细节可能不一定清楚。本文将介绍一下在Linux平台下函数栈是如何实现的。
栈帧的结构
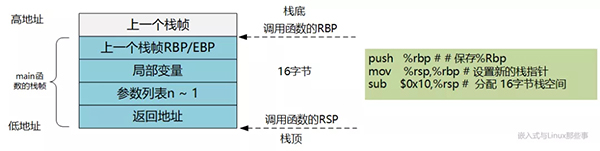
函数在调用的时候都是在栈空间上开辟一段空间以供函数使用,所以,我们先来了解一下通用栈帧的结构。
如图所示,栈是由高地址向地地址的方向生长的,而且栈有其栈顶和栈底,入栈出栈的地方就叫做栈顶。
在x86系统的CPU中,rsp是栈指针寄存器,这个寄存器中存储着栈顶的地址。rbp中存储着栈底的地址。函数栈空间主要是由这两个寄存器来确定的。
当程序运行时,栈指针rsp可以移动,栈指针和帧指针rbp一次只能存储一个地址,所以,任何时候,这一对指针指向的是同一个函数的栈帧结构。
而帧指针rbp是不移动的,访问栈中的元素可以用-4(%rbp)或者8(%rbp)访问%rbp指针下面或者上面的元素。
在明白了这些之后,下面我们来看一个具体的例子:
- #include <stdio.h>
- int sum (int a,int b)
- {
- int c = a + b;
- return c;
- }
- int main()
- {
- int x = 5,y = 10,z = 0;
- z = sum(x,y);
- printf("%d\r\n",z);
- return 0;
- }
反汇编如下,下面我们就对照汇编代码一步一步分析下函数调用过程中栈的变化。
- 0000000000000000 <sum>:
- 0: 55 push %rbp
- 1: 48 89 e5 mov %rsp,%rbp
- 4: 89 7d ec mov %edi,-0x14(%rbp) # 参数传递
- 7: 89 75 e8 mov %esi,-0x18(%rbp) # 参数传递
- a: 8b 55 ec mov -0x14(%rbp),%edx
- d: 8b 45 e8 mov -0x18(%rbp),%eax
- 10: 01 d0 add %edx,%eax
- 12: 89 45 fc mov %eax,-0x4(%rbp) # 局部变量
- 15: 8b 45 fc mov -0x4(%rbp),%eax # 存储结果
- 18: 5d pop %rbp
- 19: c3 retq
- 000000000000001a <main>:
- 1a: 55 push %rbp # 保存%rbp。rbp,栈底的地址
- 1b: 48 89 e5 mov %rsp,%rbp # 设置新的栈指针。rsp 栈指针,指向栈顶的地址
- 1e: 48 83 ec 10 sub $0x10,%rsp # 分配 16字节栈空间。%rsp = %rsp-16
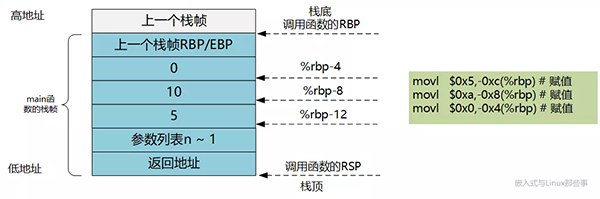
- 22: c7 45 f4 05 00 00 00 movl $0x5,-0xc(%rbp) # 赋值
- 29: c7 45 f8 0a 00 00 00 movl $0xa,-0x8(%rbp) # 赋值
- 30: c7 45 fc 00 00 00 00 movl $0x0,-0x4(%rbp) # 赋值
- 37: 8b 55 f8 mov -0x8(%rbp),%edx
- 3a: 8b 45 f4 mov -0xc(%rbp),%eax
- 3d: 89 d6 mov %edx,%esi # 参数传递 ,从右向左
- 3f: 89 c7 mov %eax,%edi # 参数传递
- 41: e8 00 00 00 00 callq 46 <main+0x2c> # 调用sum
- 46: 89 45 fc mov %eax,-0x4(%rbp)
- 49: 8b 45 fc mov -0x4(%rbp),%eax # 存储计算结果
- 4c: 89 c6 mov %eax,%esi
- 4e: 48 8d 3d 00 00 00 00 lea 0x0(%rip),%rdi # 55 <main+0x3b>
- 55: b8 00 00 00 00 mov $0x0,%eax
- 5a: e8 00 00 00 00 callq 5f <main+0x45>
- 5f: b8 00 00 00 00 mov $0x0,%eax
- 64: c9 leaveq
- 65: c3 retq
函数调用前
在函数被调用之前,调用者会为调用函数做准备。首先,函数栈上开辟了16字节的空间,存储定义的3个int型变量,建立了main函数的栈。
接着,会给三个变量进行赋值。
以下4行代码是进行参数传递。我们可以看到是函数参数是倒序传入的:先传入第N个参数,再传入第N-1个参数(CDECL约定)。
- mov -0x8(%rbp),%edx
- mov -0xc(%rbp),%eax
- mov %edx,%esi # 参数传递 ,从右向左
- mov %eax,%edi # 参数传递
最后,会执行到call指令处,调用sum函数。
- callq 46 <main+0x2c> # 调用sum
CALL指令内部其实还暗含了一个将返回地址(即CALL指令下一条指令的地址)压栈的动作(由硬件完成)。
具体来说,call指令执行时,先把下一条指令的地址入栈,再跳转到对应函数执行的起始处。
函数调用时
进入sum函数后,我们看到函数的前两行:
- push %rbp
- mov %rsp,%rbp
这两条汇编指令的含义是:首先将rbp寄存器入栈,然后将栈顶指针rsp赋值给rbp。
“mov rbp rsp”这条指令表面上看是用rsp覆盖rbp原来的值,其实不然。
因为给rbp赋值之前,原rbp值已经被压栈(位于栈顶),而新的rbp又恰恰指向栈顶。此时rbp寄存器就已经处于一个非常重要的地位。
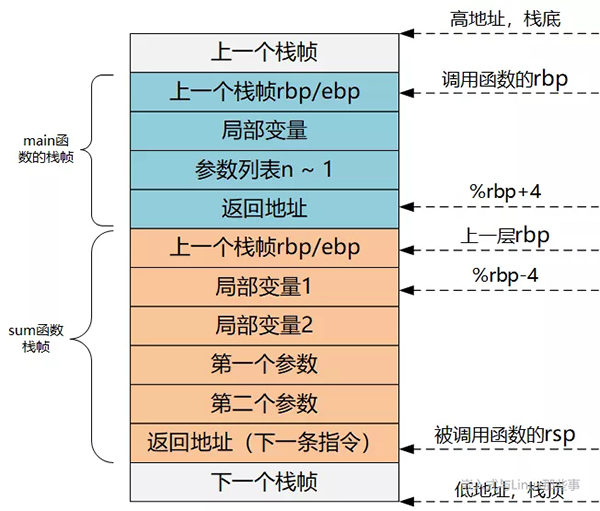
该寄存器中存储着栈中的一个地址(原rbp入栈后的栈顶),从该地址为基准,向上(栈底方向)能获取返回地址、参数值,向下(栈顶方向)能获取函数局部变量值,而该地址处又存储着上一层函数调用时的rbp值。
一般而言,%rbp+4处为返回地址,%rbp+8处为第一个参数值(最后一个入栈的参数值,此处假设其占用4字节内存),%rbp-4处为第一个局部变量,%rbp处为上一层rbp值。
由于rbp中的地址处总是“上一层函数调用时的rbp值”,而在每一层函数调用中,都能通过当时的%rbp值“向上(栈底方向)”能获取返回地址、参数值,“向下(栈顶方向)”能获取函数局部变量值。
紧接着执行的四条指令。
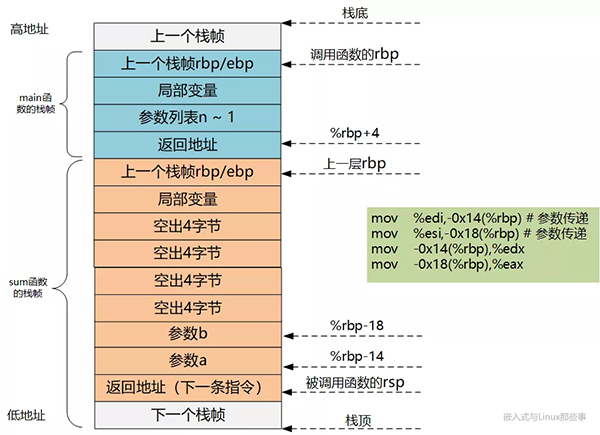
- mov %edi,-0x14(%rbp) # 参数传递
- mov %esi,-0x18(%rbp) # 参数传递
- mov -0x14(%rbp),%edx
- mov -0x18(%rbp),%eax
- add %edx,%eax
- mov %eax,-0x4(%rbp)
上述指令通过rbp加偏移量的方式将main传递给sum的两个参数保存在当前栈帧的合适位置,然后又取出来放入寄存器,看着有点儿多此一举,这是因为在编译时未给gcc指定优化级别,而gcc编译程序时,默认不做任何优化,所以看起来比较啰嗦。
需要说明的是,sum的两个参数和返回值都是int,在内存中只占4个字节,而图中每个栈内存单元按8字节地址边界进行了对齐,所以才是下图中这个样子。
再来看紧接着的三条指令。
- add %edx,%eax
- mov %eax,-0x4(%rbp) # 局部变量
- mov -0x4(%rbp),%eax # 存储结果
上述第一条指令负责执行加法运算并将并将结果存入eax中,第二条指令将eax中的值存入局部变量c所在的内存,第三条指令将局部变量c的值读取到eax中,可以看到,局部变量c被编译器安排到了%rbp -0x4这个地址对应的内存中。
接下来继续执行
- pop %rbp
- retq
这两条指令的功能相当于下面的指令:
- mov %rbp,%rsp
- pop %rbp
- pop %rip
即在操作上面两条指令的时候,首先把rsp赋值,它的值是存储调用函数rbp的值的地址,所以可以通过出栈操作,来给rbp赋值,来找回调用函数的rbp。
通过栈的结构,可以知道,rbp上面就是调用函数调用被调用函数的下一条指令的执行地址,所以需要赋值给rip,来找回调用函数里的指令执行地址。
整个函数跳转回main的时候,他的rsp,rbp都会变回原来的main函数的栈指针,C语言程序就是用这种方式来确保函数的调用之后,还能继续执行原来的程序。
函数调用后
函数最后返回的时候,继续执行下面这条指令:
- mov %eax,-0x4(%rbp) # 把sum函数的返回值赋给变量z
上述指令将eax中的结果放入rbp -0x4所指的内存中,这里也是main的局部变量z所在位置。
再往后的指令如下:
- mov %eax,-0x4(%rbp)
- mov -0x4(%rbp),%eax # 计算结果
- mov %eax,%esi
- mov %eax,%esi
- lea 0x0(%rip),%rdi
- mov $0x0,%eax
- callq 5f <main+0x45>
上述指令首先为printf准备参数,然后调用printf,具体过程和调用sum的过程相似,让CPU直接执行到main倒数第二条leave指令处。
- mov $0x0,%eax
指令作用是将main返回值0放到寄存器eax,等main返回后调用main可拿到这个值。
执行leave指令相当于执行如下两条指令:
- mov %rbp, %rsp
- pop %rbp
leave指令首先将rbp的值复制给rsp,rsp就指向rbp所指的栈单元。之后leave指令将该栈单元的值pop给rbp,如此,rsp和rbp就恢复成刚进入main时的状态。