arXiv上2021年12月19日上传论文“Topology Preserving Local Road Network Estimation from Single Onboard Camera Image“,作者来自瑞士ETH和比利时鲁汶大学。
道路网络拓扑知识对于自主规划和导航至关重要。然而,从一张图像恢复这样的拓扑结构只是部分探索。此外,需要参考一下地平面,在上面会执行驾驶动作。本文旨在直接在鸟瞰图(BEV)提取复杂城市环境的局部道路网络拓扑。唯一的输入由单个车载前视摄像头图像组成。用一组有向车道曲线表示道路拓扑,其交互是交点来捕获。为了更好地捕捉拓扑信息,引入最小循环(minimal cycles)及其覆盖(cover)的概念。最小循环是由有向曲线段(两个交点之间)形成的最小循环。覆盖是形成最小循环的一组曲线。首先证明覆盖足以唯一地表示道路拓扑,然后与车道曲线监控一起用于监督深层神经网络,学习从单个输入图像去预测道路拓扑。在NuScenes和Argoverse做了基准测试,源代码将公开。
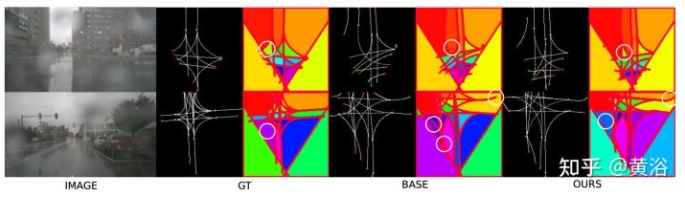
如图所示:道路网络和生成的封闭区域(最小循环,以不同颜色显示)。在道路网中,交通流从绿点流向红点,黄点是两条中心线的连接点。要学习保持包含最小循环的中心线本身。一些有趣的区域在彩色图像上以白圈显示。
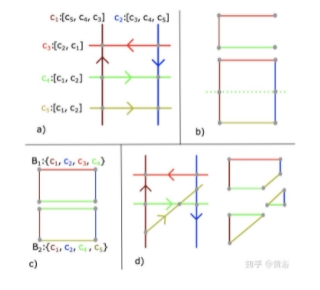
如图是最小循环及其覆盖的定义示意:c)和d)
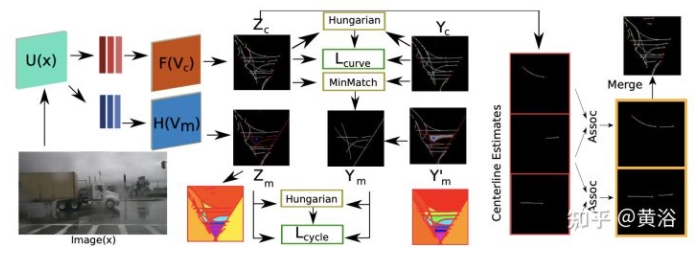
如图所示是一个训练程序:其生成中心线曲线估计值以及最小循环和覆盖;曲线和循环之间的映射提供了一致和更高级的监督,得到对场景拓扑的理解;将连接步用于每对选定曲线,估计连接性概率,其中修改连接的中心线使其对应端点重合。
用神经网络预测固定数量的曲线和最小循环,其大于场景中的实际曲线数和循环数。因此,假设有一个函数U接受输入(相机图像)并输出两个矩阵,一个是所有N条曲线候选的D维嵌入,另一个是所有M个最小循环候选的E维嵌入。这两个嵌入矩阵分别由函数F(Vc)和H(Vm)处理。F(Vc)处理嵌入Vc的候选曲线并生成矩阵输出,其包含N条曲线的参数和曲线存在的概率。H(Vm)处理最小循环候选嵌入,并生成三个输出,每个输出描述最小循环的属性。第一是M条候选曲线中每一条的估计最小覆盖,描述N条候选曲线和K个FOV边界曲线之一属于该覆盖的概率;第二是可能存在最小循环的概率,最后是辅助输出,估计候选最小循环的中心。因此,该网络最后生成一组曲线和最小循环候选。
训练中用基于匹配的方法,对曲线很简单,控制点之间L1差采用匈牙利匹配;然而,对最小循环来说,更为复杂;其中基本的一点是,真实拓扑和估计拓扑之间的匹配是一致的。
设有N′个真曲线和带K边界曲线的M′个真最小循环。同样,记录真曲线参数、真曲线的最小覆盖和真的最小循环中心。由于真值(GT)最小循环定义在真曲线上,而检测到的最小循环定义在估计曲线上,因此必须首先在估计曲线和真曲线之间形成匹配。匈牙利匹配是不理想的,因为它不考虑估计曲线的碎片化。碎片是指多条相连的估计曲线代表一条真曲线的情况。因此,通常情况下,估计的候选最小循环比真的最小循环有更多的候选曲线。
由于匈牙利算法的“一对一”匹配特性,一条长真曲线只能与一条短片段曲线匹配,即使估计片段的组合可以得到更接近的近似。因此,将每个候选曲线与其最近的真曲线进行匹配,这意味着每一条候选曲线只匹配一条真曲线,而真曲线可以匹配任意数量(包括零个)的候选曲线。
将所有匹配的估计曲线设置为一,如果它们对应的真实曲线存在于最小循环中。鉴于此修正的真最小循环标签和估计的最小循环,运行匈牙利匹配可以找到用于损失计算的那对,这使得估计的拓扑得到一致的训练。
最后,为了监控曲线的连通性,显式地估计网络中V(G,E)的关联矩阵A。为每个候选中心线提取一个特征向量并构建一个分类器实现这个估计,该分类器采用属于一对曲线的两个特征向量,并输出它们的关联概率。
训练中使用匈牙利算法匹配的曲线建立正确的顺序。估计的关联矩阵还允许在测试期间进行合并后处理,其中会修改曲线的端点,以便使相连接的曲线重合在一起。
中心线的样条曲线控制点和最小循环中心使用L1 -loss进行训练,同时用中心线和最小循环概率的二元交叉熵。二元交叉熵计算最小循环的membership-loss以及连通性。
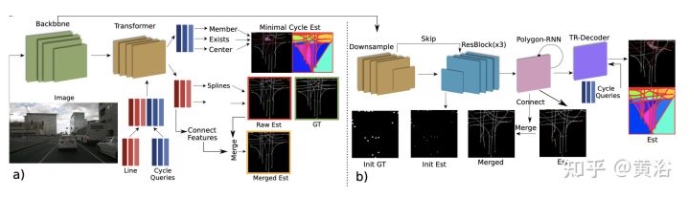
如图是设计的网络架构:(a)最小循环Transformer网络和(b)最小循环多边形RNN网络;第一个联合处理两组查询(曲线和最小循环)以生成相应的特征向量。然后将这些向量馈送给MLP进行最终估计;第二个是三部分组成:1)初始点估计,2)给定初始点,可以输出曲线后续控制点的多边形RNN,以及 3)最小循环的解码器。
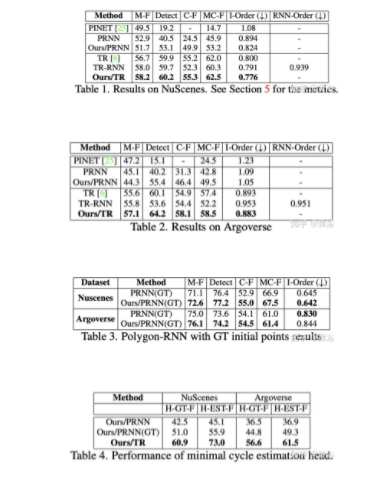
提出了道路拓扑准确性的两个测度:Minimal-Cycle Minimal Cover (B) 和Intersection Order。
实验结果如下;
局限性:对于大多数现代道路网络,这里的理论假设都是温和的。然而,有可能存在违反这些假设的情况,这样的道路网对网络进行训练非常困难。此外,提取用于训练的最小循环是一个耗时的过程,并会阻止使用数据增强技术。