AI生成高数题，难出新高度：MIT提出可出题做题、评分的算法模型

就在 2021 年的最后一天， MIT 与哥伦比亚大学、哈佛大学、滑铁卢大学的联合研究团队发表了一篇长达 114 页的论文，提出了首个可以大规模自动解决、评分和生成大学水平数学问题的模型，可以说是人工智能和高等教育的一个重要里程碑。其实在这项研究之前，人们普遍认为神经网络无法解决高等数学问题。

值得一提的是，该研究用到了 OpenAI 的 Codex。

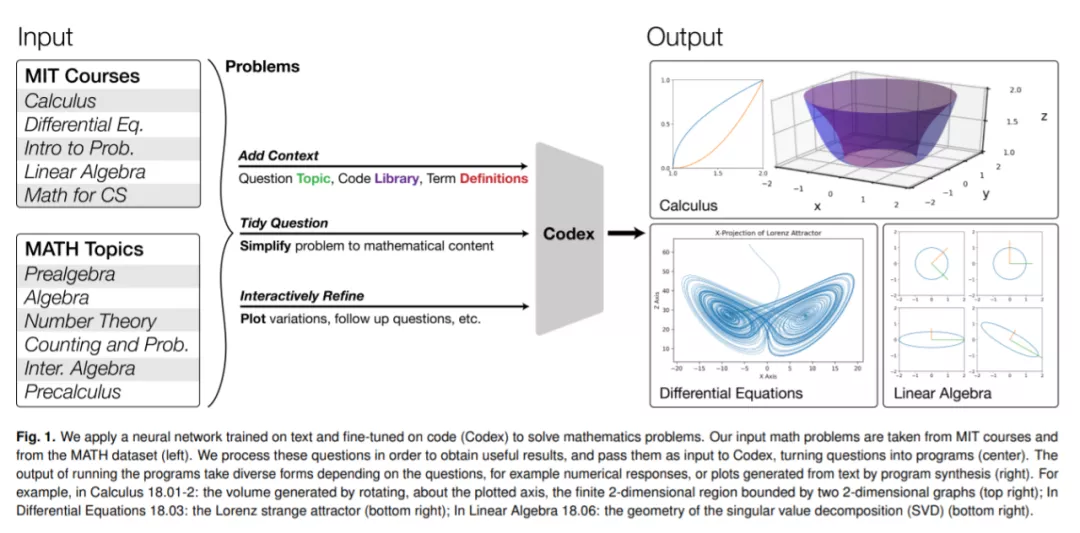
这项研究有多厉害呢？我们以下图为例，下图展示了计算洛伦茨吸引子及其投影，计算和演示奇异值分解 (SVD) 方法的几何形状等。机器学习模型很难解决上述问题，但这项研究表明它们不仅可以解决这些问题，还可以大规模解决所属课程以及许多此类课程问题。

该研究表明对文本进行预训练并在代码上进行微调的神经网络，可以通过程序合成（program synthesis）解决数学问题。具体而言，该研究可将数学问题转化为编程任务，自动生成程序，然后执行，以解决 MIT 数学课程问题和来自 MATH 数据集的问题。其中，MATH 数据集是专门用于评估数学推理的高等数学问题最新基准，涵盖初级代数、代数、计数与概率、数论与微积分。

此外，该研究还探索了一些提示（prompt）生成方法，使 Transformer 能够为相应主题生成问题解决程序，包括带有图象的解决方案。通过量化原始问题和转换后的提示之间的差距，该研究评估了生成问题的质量和难度。

论文地址：https://arxiv.org/pdf/2112.15594.pdf

方法

数据集

该研究首先从 MIT 的以下六门课程中，每门课程随机选取了 25 个问题：

• 单变量微积分；
• 多元微积分；
• 微分方程；
• 概率与统计概论；
• 线性代数；
• 计算机科学数学。

对于 MATH 数据集，该研究从每个主题中随机抽取 5 个问题，并通过在应用线性代数新课程 COMS3251 上的实验验证了该方法的结果不仅仅是过拟合训练数据。

方法流程

如下图 2 所示，该研究使用 Codex 将课程问题转换为编程任务并运行程序以解决数学问题。下图共包含 A-E 5 个面板，每个面板的左侧部分显示了原始问题和重新表述的提示，其中提示是通过添加上下文、交互、简化描述等形成的。

该研究将从原始课程问题到 Codex 提示的转换分为以下三类：

• 原生提示：Codex 提示和原始问题相同；
• 自动提示转换：Codex 提示和原始问题不同，由 Codex 自动生成；
• 手动提示转换：Codex 提示和原始问题不同，由人工生成。

问题与提示之间的差距

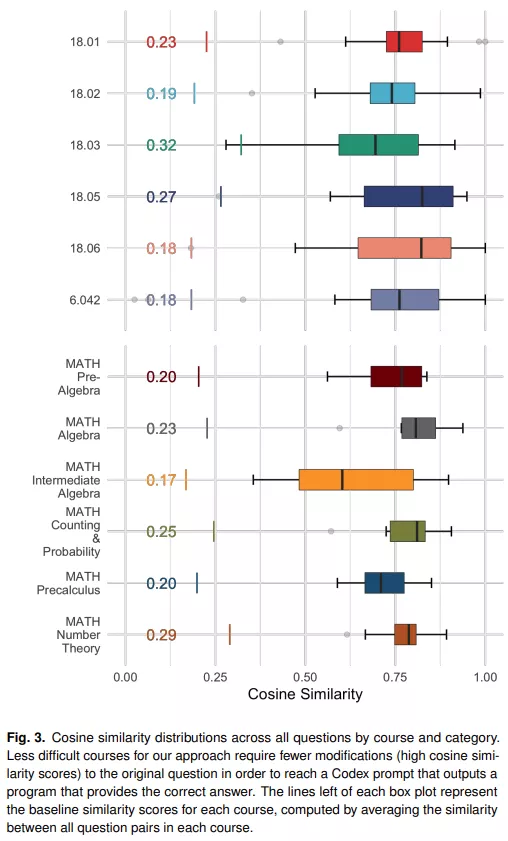
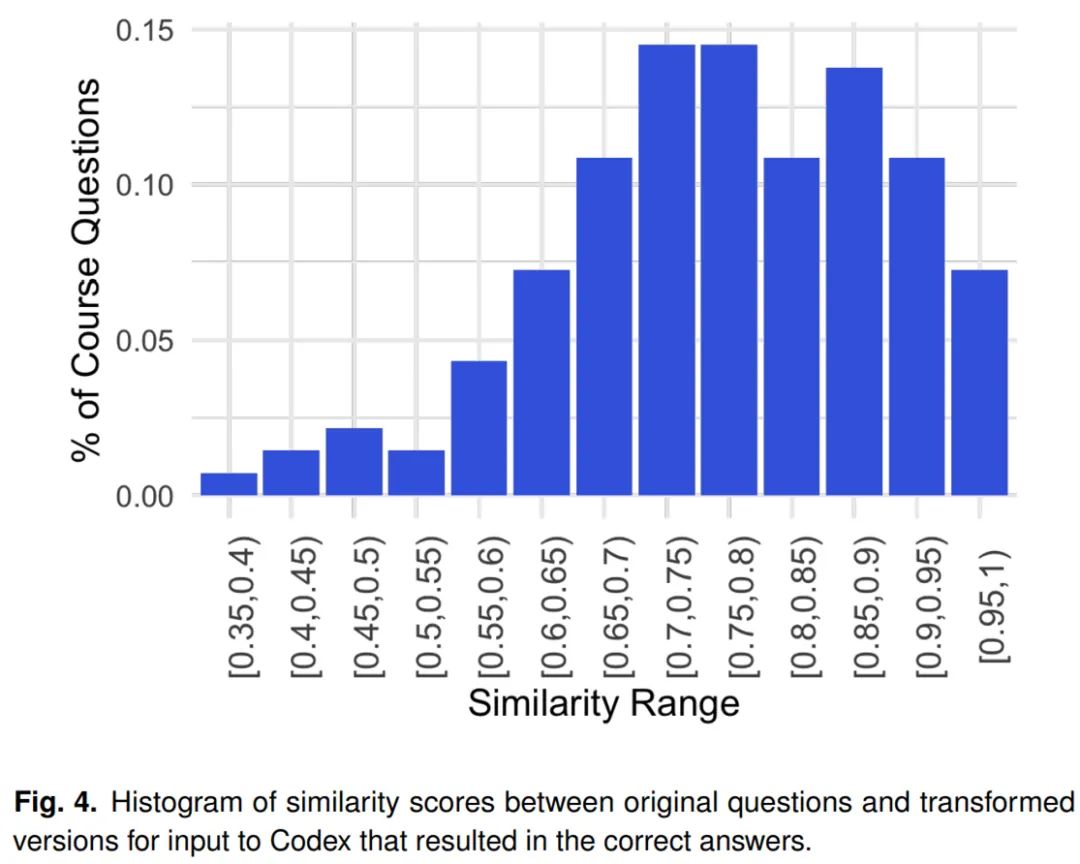
将问题转换为 Codex 提示的关键是：从语义上讲，原始问题与产生正确解决方案的提示之间的接近程度。为了度量原始问题和成功提示之间的差距，该研究使用 Sentence-BERT 嵌入之间的余弦相似度，如下图 3 所示。

Sentence-BERT 使用 siamese 和 triplet 神经网络结构对预训练的 BERT 模型进行微调。其中至关重要的是，Sentence-BERT 能够在句子级别生成语义嵌入，从而可以在长文本之间进行语义相似性比较。

在该研究的实验中，原始问题和生成正确答案的提示之间的相似度如下图 4 所示。

Codex 用于提示生成

在某些课程中，直接使用未转换的原始问题提示 Codex，无法产生正确的解决方案。因此，需要将原始问题转化为 Codex 可以处理的形式，主要分为以下三类：

• 主题上下文形式：该形式为 Codex 提供了与一般课程和特定问题相关的主题和子主题，以帮助指导 Codex 生成相关正确的答案。例如，对于概率中的条件期望问题，提供有关贝叶斯定理、期望等的上下文信息会很有帮助。
• 库上下文：该形式为 Codex 提供了解决给定问题所需的编程包 / 库。例如，指导 Codex 使用 Python 中的 numpy 包来解决线性代数问题。
• 定义上下文：很多时候，Codex 对某些术语的定义缺乏现实背景。举例来说，Codex 不理解扑克牌中的 Full House 是什么意思。因此让 Codex 理解这些术语并明确定义，可以更好地指导其程序合成。

生成问题以及人类评估

该研究使用 Codex 为每门课程生成新的问题，通过数据集创建有编号的问题列表来完成，这个列表在生成随机数量的问题之后会被截断断，结果将用于提示 Codex 生成下一个问题。不断的重复这个过程，就可以为每门课程产生许多新的问题。

该研究对参加过这些课程或同等课程的、来自 MIT 和哥伦比亚大学的学生进行了一项长期调查。调查的目的是比较每门课程机器生成的问题与人工编写的问题的质量和难度。该研究为每门 MIT 的课程随机抽取五个原始问题和五个生成的问题。在调查中，学生被要求阅读每门课程的十个问题，这些问题是人工编写的问题和机器生成的问题的混合。

对于 60 个问题中的每一个，学生都被问到三个问题，如图 5 所示：他们是否认为给定的问题是 (i) 人工编写的或机器生成的，(ii) 适合或不适合特定课程，以及 (iii) ) 在 1（最简单）和 5（最难）之间的范围内，问题的难度级别是多少。要求学生提供他们对数学问题的评分，而不是解决这些问题。该调查以在线和匿名的形式提供。

调研结果

问题求解

研究者共求解了补充资料中展示的 210 个问题，其中包括 6 门课程各自对应的 25 个随机问题以及 MATH 数据集中 6 个主题（初级代数、代数、数论、计数与概率、中极代数、微积分）各自对应的 10 个随机问题。

生成新问题

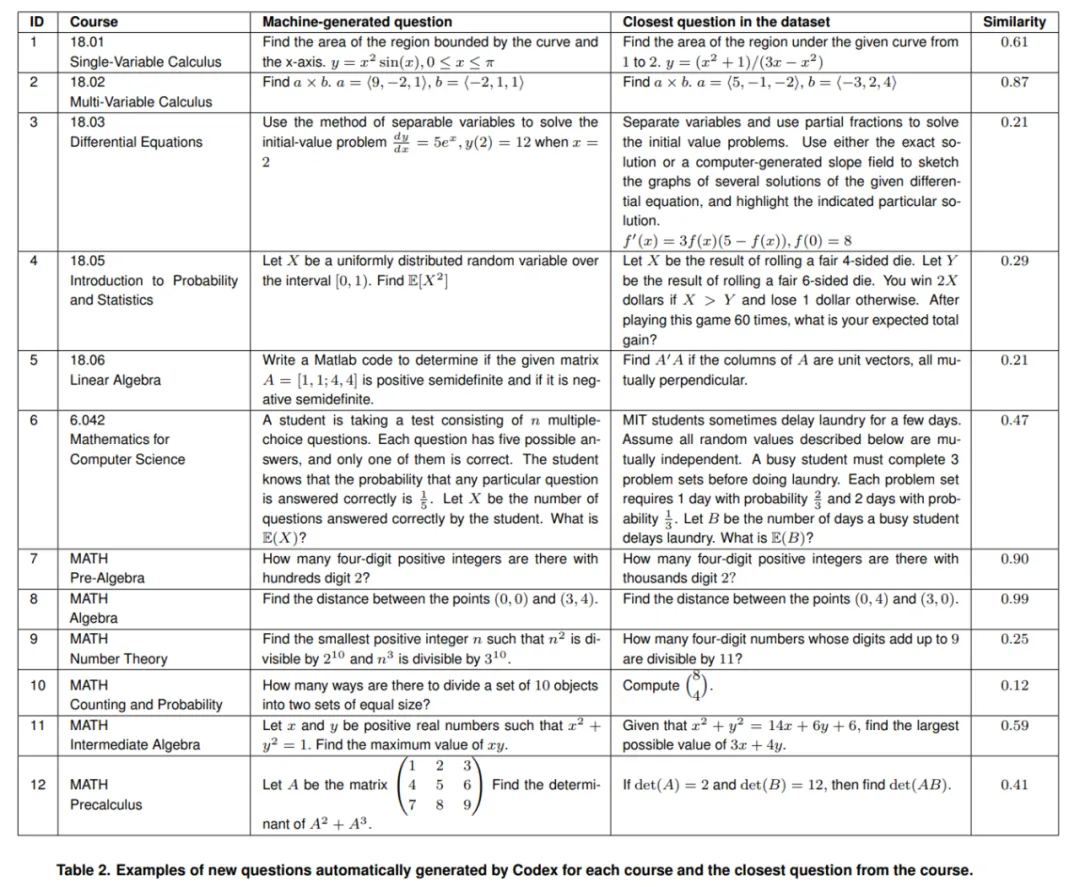
研究者生成了 120 个新问题，其中包括 6 门课程和 6 个 MATH 主题各自对应的 10 个新问题。下表 2 展示了每门课程和每个 MATH 主题对应的一个生成问题。生成一个问题只需不到 1 秒的时间，研究者可以生成任意数量的问题。他们为 Codex 能够生成正确答案的 25 个随机选择的问题创建了提示，切入随机问题，并让 Codex 完成下一个新问题。

学生调研结果

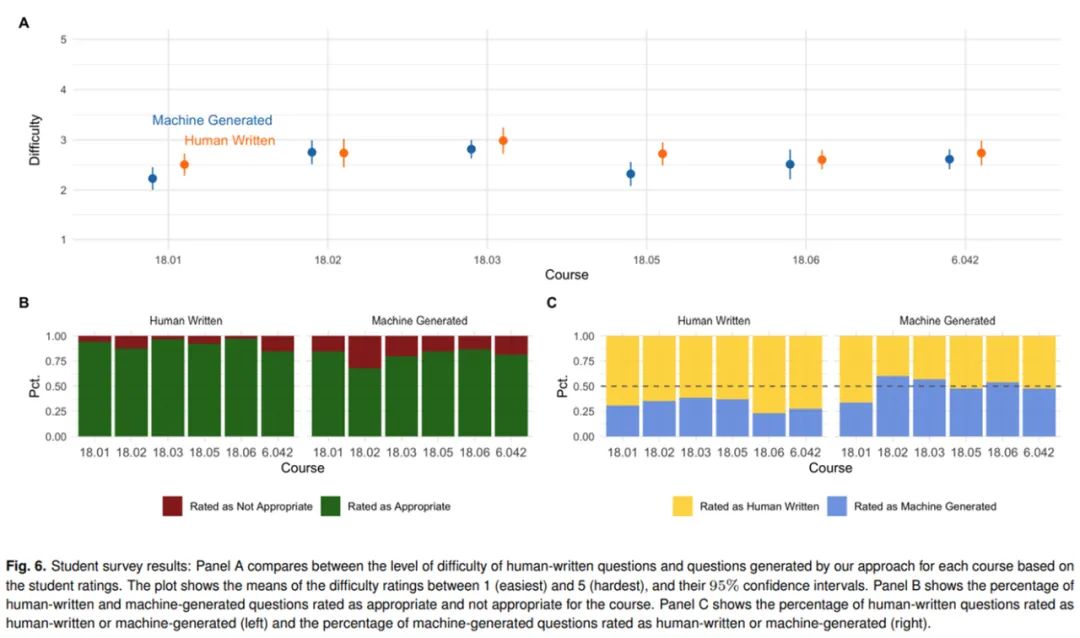
研究者表示，共有 13 位参与者完成了全部 60 个问题的问答调研，平均耗时 40 分钟。下图 6 总结了学生调研中人工编写（human-written）和机器生成（machine-generated）问题的比较情况，并得出了以下几项结果：

• 机器生成的问题要比人工编写的问题难度高，但在置信区间内；
• 人工编写的问题要比机器生成的问题更适合课程；
• 人工编写的问题更容易被认为人写的，并且将机器生成问题看作机器生成和人工编写的概率相同。

答案定级

Codex 能够回答所有随机采样的大学水平和 MATH 数据集数学问题，无论它们是原始状态还是整理后状态。

挑战

研究者的方法还有一些无法解决的技术障碍。

1、输入图像。Codex 的一个基础限制是它只能接收基于文本的输入。因此，Codex 无法使用图形或图表等必要的视觉组件来回答问题。

2、高等数学证明。这项研究的另一个限制是缺乏对高等数学的证明。研究者强调称，这是由研究自身的广度而不是 Codex 的证明能力导致的。事实上，该研究中提交至 Codex 的大多数简单分析证明都已成功地被执行，这令人震惊，因为证明通常不是基于代码的。

3、程序评估。该研究的最后一步是执行程序，例如使用 Python 解释器。参加大学水平课程的学生也会编写代码来解决他们的部分问题。因此，该研究以与人类学生相同的方式测试神经网络解决问题的能力，让他们使用必要的工具。还有关于神经程序评估的工作，演示了使用机器学习来预测程序输出。LSTM 用于成功预测某些线性时间和恒定空间程序的输出 (18)。这些都增加了内存暂存器以允许更大的程序类别 (19)。最近的方法使用因果 GNN (20) 和 transformer (21)。尽管评估任意代码是不可判定的，但特殊情况，例如由另一个 transformer 生成的用于解决简单数学问题的程序，原则上应该是可学习的。

4、理论复杂性。计算复杂度的结果表明，该研究无法解决大学数学课程中一般问题的每一个具体实例。例如，以下问题具有难以处理的结果：向量 v 可以表示为来自集合 S 的向量之和吗？以下一阶微分方程的解是什么？但是，我们知道作业和考试给出的问题可以由人类解决，因此这些复杂性结果不适用于该研究的特定实例解决。