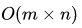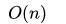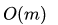一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
- 输入:m = 3, n = 7
- 输出:28
示例 2:
- 输入:m = 2, n = 3
- 输出:3
解释:从左上角开始,总共有 3 条路径可以到达右下角。
- 向右 -> 向右 -> 向下
- 向右 -> 向下 -> 向右
- 向下 -> 向右 -> 向右
示例 3:
- 输入:m = 7, n = 3
- 输出:28
示例 4:
- 输入:m = 3, n = 3
- 输出:6
提示:
- 1 <= m, n <= 100
- 题目数据保证答案小于等于 2 * 10^9
思路
深搜
这道题目,刚一看最直观的想法就是用图论里的深搜,来枚举出来有多少种路径。
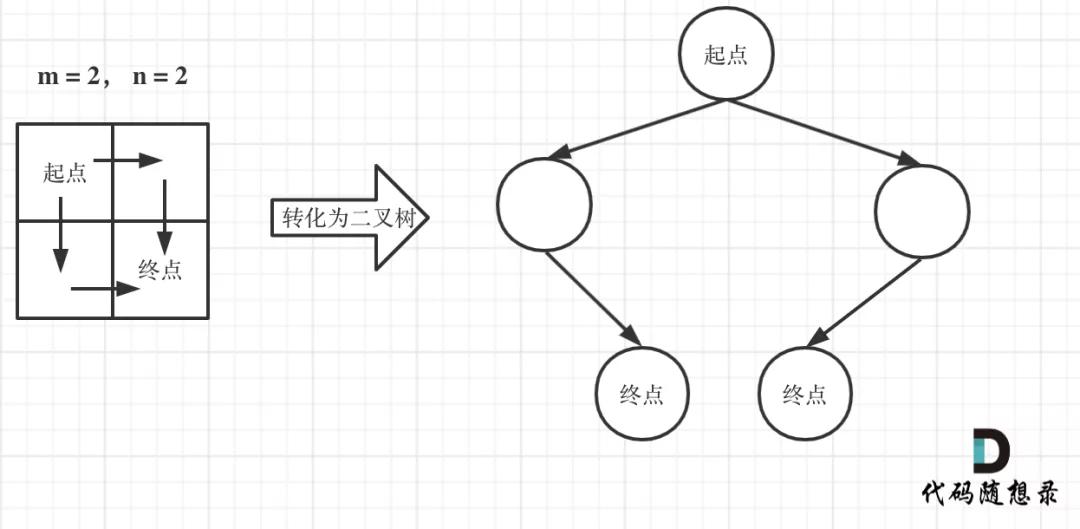
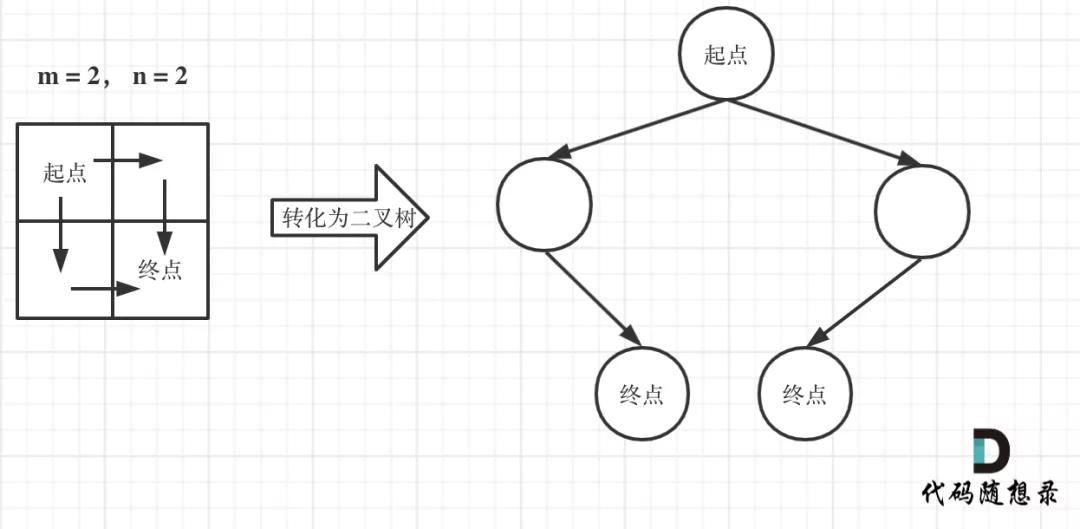
注意题目中说机器人每次只能向下或者向右移动一步,那么其实机器人走过的路径可以抽象为一颗二叉树,而叶子节点就是终点!
如图举例:
不同路径
此时问题就可以转化为求二叉树叶子节点的个数,代码如下:
- class Solution {
- private:
- int dfs(int i, int j, int m, int n) {
- if (i > m || j > n) return 0; // 越界了
- if (i == m && j == n) return 1; // 找到一种方法,相当于找到了叶子节点
- return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n);
- }
- public:
- int uniquePaths(int m, int n) {
- return dfs(1, 1, m, n);
- }
- };
大家如果提交了代码就会发现超时了!
来分析一下时间复杂度,这个深搜的算法,其实就是要遍历整个二叉树。
这颗树的深度其实就是m+n-1(深度按从1开始计算)。
那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树(其实没有遍历整个满二叉树,只是近似而已)
所以上面深搜代码的时间复杂度为,可以看出,这是指数级别的时间复杂度,是非常大的。
动态规划
机器人从(0 , 0) 位置出发,到(m - 1, n - 1)终点。
按照动规五部曲来分析:
确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
确定递推公式
想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]。
此时在回顾一下 dp[i - 1][j] 表示啥,是从(0, 0)的位置到(i - 1, j)有几条路径,dp[i][j - 1]同理。
那么很自然,dp[i][j] = dp[i - 1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来。
dp数组的初始化
如何初始化呢,首先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。
所以初始化代码为:
- for (int i = 0; i < m; i++) dp[i][0] = 1;
- for (int j = 0; j < n; j++) dp[0][j] = 1;
确定遍历顺序
这里要看一下递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
这样就可以保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。
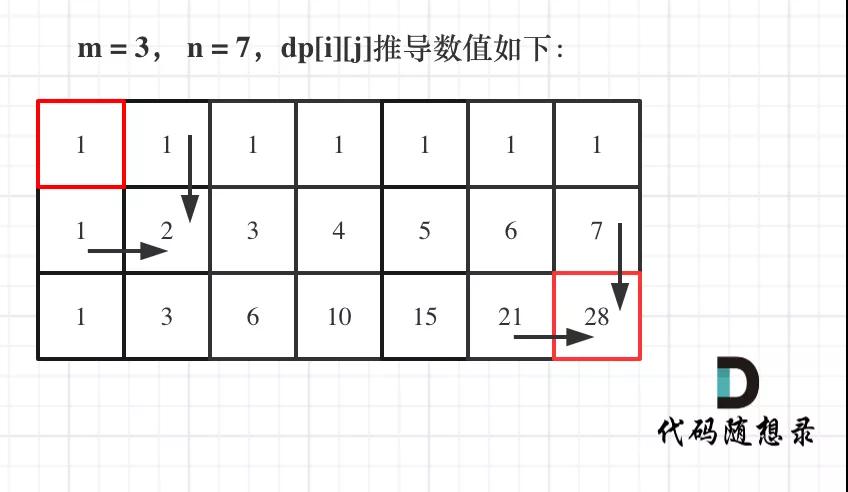
举例推导dp数组
如图所示:
不同路径
以上动规五部曲分析完毕,C++代码如下:
- class Solution {
- public:
- int uniquePaths(int m, int n) {
- vector<vector<int>> dp(m, vector<int>(n, 0));
- for (int i = 0; i < m; i++) dp[i][0] = 1;
- for (int j = 0; j < n; j++) dp[0][j] = 1;
- for (int i = 1; i < m; i++) {
- for (int j = 1; j < n; j++) {
- dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
- }
- }
- return dp[m - 1][n - 1];
- }
- };
其实用一个一维数组(也可以理解是滚动数组)就可以了,但是不利于理解,可以优化点空间,建议先理解了二维,在理解一维,C++代码如下:
- class Solution {
- public:
- int uniquePaths(int m, int n) {
- vector<int> dp(n);
- for (int i = 0; i < n; i++) dp[i] = 1;
- for (int j = 1; j < m; j++) {
- for (int i = 1; i < n; i++) {
- dp[i] += dp[i - 1];
- }
- }
- return dp[n - 1];
- }
- };
数论方法
在这个图中,可以看出一共m,n的话,无论怎么走,走到终点都需要 m + n - 2 步。
不同路径
在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。
那么有几种走法呢?可以转化为,给你m + n - 2个不同的数,随便取m - 1个数,有几种取法。
那么这就是一个组合问题了。
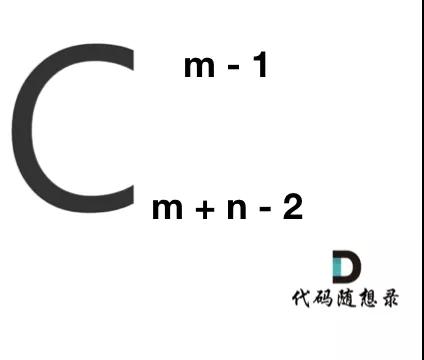
那么答案,如图所示:
不同路径
求组合的时候,要防止两个int相乘溢出! 所以不能把算式的分子都算出来,分母都算出来再做除法。
例如如下代码是不行的。
- class Solution {
- public:
- int uniquePaths(int m, int n) {
- int numerator = 1, denominator = 1;
- int count = m - 1;
- int t = m + n - 2;
- while (count--) numerator *= (t--); // 计算分子,此时分子就会溢出
- for (int i = 1; i <= m - 1; i++) denominator *= i; // 计算分母
- return numerator / denominator;
- }
- };
需要在计算分子的时候,不断除以分母,代码如下:
- class Solution {
- public:
- int uniquePaths(int m, int n) {
- long long numerator = 1; // 分子
- int denominator = m - 1; // 分母
- int count = m - 1;
- int t = m + n - 2;
- while (count--) {
- numerator *= (t--);
- while (denominator != 0 && numerator % denominator == 0) {
- numerator /= denominator;
- denominator--;
- }
- }
- return numerator;
- }
- };
计算组合问题的代码还是有难度的,特别是处理溢出的情况!
总结
本文分别给出了深搜,动规,数论三种方法。
深搜当然是超时了,顺便分析了一下使用深搜的时间复杂度,就可以看出为什么超时了。
然后在给出动规的方法,依然是使用动规五部曲,这次我们就要考虑如何正确的初始化了,初始化和遍历顺序其实也很重要!