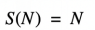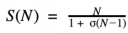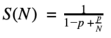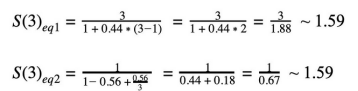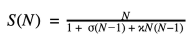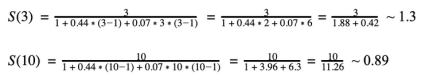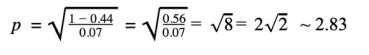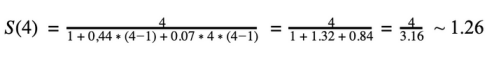【51CTO.com快译】本文将介绍如何通过数学方程来描述系统——至少在某种程度上是这样的。人们将熟悉诸如争用、一致性和相关性延迟之类的术语。此外,还将展示可以帮助计算这三种机制对应用程序影响的定律及其数学方程。
这篇文章侧重于整体系统设计和架构,并将尝试回答“可以无限地扩展系统吗?”这个问题。
然而,为了充分理解这个主题,将首先回答一个更简单的问题:什么是可扩展性?
什么是可扩展性?
可扩展性的最佳定义之一可以在维基百科中找到,可以这样引用:通过添加更多资源来处理越来越多的工作的系统属性(...)
从这样的声明中,可以预期,如果软件系统被认为是可扩展的,可以添加越来越多的资源(线程、CPU、节点),并可能处理任何增加的传入流量。然而,这仅适用于理想世界。在令人失望的现实中,必须考虑以上提到的三个概念。在开始解释它为什么采用这种方式之前,先介绍有关线性可扩展性的细节。
线性可扩展性
一般来说,这是想要实现的最佳情况。在这里,当向系统添加资源时,它总是会导致其性能提升。更重要的是,可以无限期地做到这一点,而不会受到任何负面影响。可以用来计算线性可扩展性影响的数学方程非常小且简单。
线性可扩展性方程
S→整体任务的执行时间整体提升
N→改进的资源(线程、CPU、节点)
现在可以看到,执行时间的整体改进只取决于改进的资源,所以添加的资源越多,获得的性能提升就越大。不幸的是,如上所述,在更复杂的系统中几乎不可能出现这种情况。
在对线性可扩展性进行了简要介绍之后,可以进一步探讨其他主题,先从争用开始。
什么是争用?
简单地说,这是对共享资源访问权的竞争。几乎所有东西都可以是这样的资源,从像CPU周期这样的低级资源到像数据库访问线程这样的高级资源,甚至是更高的抽象资源(例如系统套接字)。
就像每场比赛一样都只有一名获胜者一样,但更重要的是,在“获胜者”胜出之后,其余的“参与者”必须等待,仍在利用和封锁他们的资源,等待“获胜者”完成任务之后,然后从头开始进行比赛。
同样,与任何其他比赛一样,拥有的竞争者越多,成为最终获胜者所需的时间就越多。在面向软件的世界中,这意味着当将系统置于足够的负载时,可以预期所有可接受的时间限制都将被打破。与此同时,系统将继续利用其他地方可能需要的资源,这可能会导致越来越多的故障。
在任何类型的线程池的情况下,情况似乎更加复杂。在那里,可以看到最终有多个赢家的情况,因为有很多线程在线程池中,并且有多个输家。此外,在这种情况下选择下一个获胜者的过程与特定的线程池实施密切相关。
现在,当知道什么是争用以及它可能如何影响应用程序之后,继续描述第一条定律。
什么是阿姆达尔定律?
阿姆达尔定律是由吉恩·阿姆达尔于1967年提出的。它描述了在资源得到改进的系统中,在固定负载下任务执行延迟的理论改进——例如在多线程的情况下,这里指的是添加更多线程。
简而言之,它可以用来计算通过向系统添加更多资源而获得的最大改进。在这里至关重要的是,只有使用特定资源的代码才能从这种资源改进中获益,这是一个非常合乎逻辑的结论,因此受到非获益部分的执行时间的限制。
例如:
如果想向系统添加更多线程,只有多线程的部分才能从这些操作中受益,而且将会受到单线程部分的执行时间的限制。
阿姆达尔定律方程
S→整体任务执行时间整体提升
σ→未受益于改进资源的部分最初占用的执行时间比例
N→改进的资源(线程、CPU、节点)
当参数(σ)设置为0时,阿姆达尔定律将自身简化为线性可扩展方程形式。
可以将σ替换为(1-p),并在转换后得到另一个与上述公式类似的方程:
p→受益于改进资源的部分原先占用的执行时间比例。
与p=1时的σ=0类似,阿姆达尔定律将自身简化为线性可扩展方程形式。这两种情况都描述了当整个应用程序受益于改进资源时的最大潜在好处。
需要记住的是,这两个方程是相等的,并且应该为各自的数据返回相同的结果。将在示例中包括计算。
例子:
例如有一项工作运行了9个小时。假设5小时长的部分可以并行化和改进,改进后的速度将是之前的三倍。
现在知道:
N=3
p=5/9=0.56
σ=4/9=0.44
所以
如上所见,在这种情况下,将能够比以前快0.59倍(大约6小时3分钟)完成任务。
这里有两个值得注意的事情:
(1)如果整个程序受益于系统资源改进,S最多可以等于3;σ=0|p=1。
(2)受益部分越大,改善越大。
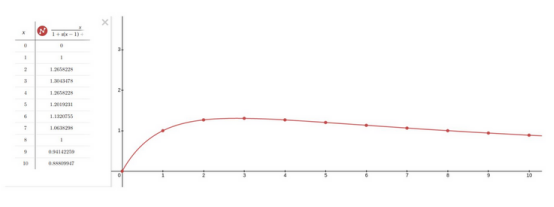
在上图中,可以看到N从0到10的绘制图,σ=0.44,这适用于阿姆达尔定律。
阿姆达尔定律和争用
由于争用使每个请求者的可用资源越来越少,从而限制了系统的并行化,因此可以看到,代码库越有争议,改进所产生的整体影响就越小。
在解释了争用、争用对软件的影响以及如何计算争用之后,可以转向需要讨论的第二个概念。
什么是一致性?
一致性是指处理读/写的顺序,以确保以合理的顺序查看这两个操作。它是整个系统设计中最重要的主题之一。这就是它在字母C下的CAP定理中找到了其表示的原因。两个最重要的一致性模型是最终一致性和强一致性。还有其他一致性模型,但它们不那么重要。
什么是相关性?
相关性是一个与一致性密切相关的术语,是关于确保任何相关方在给定时刻看到处于相同状态的同一特定数据段。对于在两个或多个节点之间共享其部分状态的所有系统来说,这是一个至关重要的概念。
什么是相关性延迟?
如果相关性是为了确保对状态特定部分的任何请求返回相同的值,那么相关性延迟可以被视为达到系统范围一致性所需的时间。
这里值得一提的是,向系统添加更多节点会增加相关性延迟的时间。
相关性延迟和冈瑟定律
冈瑟定律或通用可扩展性定律(USL)由尼尔·冈瑟于1993年制定。它建立在阿姆达尔定律之上,但另外,它考虑了由于进程间通信引起的开销。
通俗地说,它允许计算系统的可扩展性,同时考虑并发性、争用(阿姆达尔定律)和相关性延迟,使最终结果更符合实际情况。事实上,由于在方程中引入了相关性延迟,能够看到尝试扩大系统的负面结果。
冈瑟定律方程
S→整体任务执行时间整体提升。
σ→未受益于改进资源的部分最初占用的执行时间比例。
κ→系统用于实现一致性的执行时间比例,即相关性延迟;没有办法计算它,必须测量它或者只是通过在等式中放置不同的值来试验它,查看系统可以扩展的程度。
N→改进的资源(线程、CPU、节点)
当描述相关性延迟(κ)的参数设置为0时,冈瑟定律将自身简化为阿姆达尔定律方程形式。
例子:
数据与阿姆达尔定律的数据相同,但此外,系统将其正常运行时间的7%用于使其状态保持一致。
N=3
σ=4/9=0.44
κ=0.07
那么根据上面的计算可以做什么呢?
(1)性能改进有所下降,而不是0.59改进,只有0.30的提升。
(2)如果继续给系统增加资源,可以看到性能下降而不是增加,这里可以看到当将N缩放到10时,性能下降了0.11。
(3)从计算中可以看出,相关性延迟(κ)对整体改进的影响比争用大得多。
可以在下面找到冈瑟定律的绘图,其中N从0到10,σ=0,44κ=0.07。可以看到,对于N等于9,开始注意到性能下降。
如何选择最优的N?
这个答案很简单,但需要做一些数学运算,本文中的大部分内容也是如此。首先,可以将冈瑟定律视为一个函数S(N),对于任何函数(实际上只是一部分),可以计算S(N)具有最大值的点(N)。拥有这样的价值提供了两条非常重要的信息:
(1)知道在投入使用之前需要准备多少资源。
(2)可以计算系统在当前状态下扩展的范围。
所有这一切都可以使用普通的计算器或纸笔实现,不包括计算机(取决于计算机的先进程度)。
最优N方程:
例子:
正在计算所需的节点数,以最大限度地改进冈瑟定律示例中的数据。
σ=4/9=0.44
κ=0.07
如上所见,最佳节点数为2.83,但由于无法添加部分节点,因此会添加3个节点并最终得到p=3。
为了验证它,将计算S(4),并查看使用4个节点而不是3个节点。将实现多大的改进。需要记住,S(3)=1.3。
S(4)=1.26
如上所见,S(4)比S(3)小(稍微小一些)。
回答最后的问题
可以无限扩展系统吗?当然不是。
除非系统完全无状态(这样的情况很少),否则只能将其扩展到冈瑟定律所描述的程度。如果在该限制范围内添加更多资源,最终将降低系统性能,而不是提高性能。
即使在几乎没有相关性延迟的最佳情况下,最终也会受到阿姆达尔定律的限制,这仍然远远不能达到线性可扩展性的程度,要实现这样的可扩展性,基本上必须没有状态,并且完全并行化的软件没有串行瓶颈。
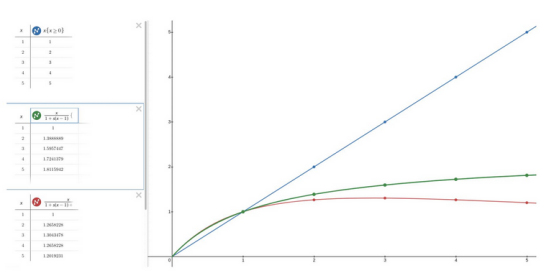
在上图中,可以看到绘制的图表:线性可扩展性(蓝线)、阿姆达尔定律(绿线)和通用的可扩展性定律(红线)从0到5。可以清楚地看到它们之间的差异,特别是它们与期望的可扩展性(线性)之间的距离。当然,N越大,这种差异就越明显。根据研究,κ参数的值没有通用规则。它的真正价值仅取决于系统的复杂性。
结论
希望通过本文可以学到有关整体系统设计的新知识,并且对将来有用。需要记住的是,可以计算可扩展性,而线性可扩展性是不可能的。
原文标题:Contention, Coherency, and Math Behind Software,作者:Bartłomiej Żyliński
【51CTO译稿,合作站点转载请注明原文译者和出处为51CTO.com】