本文介绍以下查找算法:
线性查找(Linear Search)
二分查找(Binary Search)
插值查找(Interpolation Search)
我们详细了解一下它们各自的情况。
一. 线性查找
查找数据的最简单策略就是线性查找,它简单地遍历每个元素以寻找目标,访问每个数据点从而查找匹配项,找到匹配项后,返回结果,算法退出循环,否则,算法将继续查找,直到到达数据末尾。线性查找的明显缺点是,由于固有的穷举搜索,它非常慢。它的优点是无须像其他算法那样,需要数据排好序。
我们看一下线性查找的代码:
- def LinearSearch(list, item):
- index = 0
- found = False
- # Match the value with each data element
- while index < len(list) and found is False:
- if list[index] == item:
- found = True
- else:
- index = index + 1
- return found
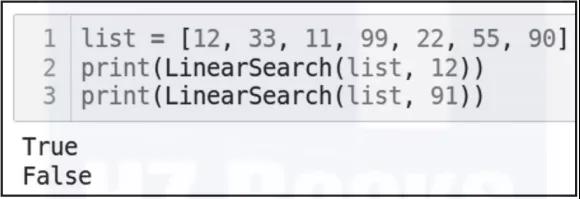
现在,看一下代码的输出(见图3-15)。
- list = [12, 33, 11, 99, 22, 55, 90]
- print(LinearSearch(list, 12))
- print(LinearSearch(list, 91))
▲图 3-15
需要注意的是,如果能成功找到数据,运行LinearSearch函数会返回True。
- 线性查找的性能:如上所述,线性查找是一种执行穷举搜索的简单算法,其最坏时间复杂度是O(N)。
二. 二分查找
二分查找算法的前提条件是数据有序。算法反复地将当前列表分成两部分,跟踪最低和最高的两个索引,直到找到它要找的值为止:
- def BinarySearch(list, item):
- first = 0
- last = len(list)-1
- found = False
- while first<=last and not found:
- midpoint = (first + last)//2
- if list[midpoint] == item:
- found = True
- else:
- if item < list[midpoint]:
- last = midpoint-1
- else:
- first = midpoint+1
- return found
输出结果如图3-16所示。
- list = [12, 33, 11, 99, 22, 55, 90]
- sorted_list = BubbleSort(list)
- print(BinarySearch(list, 12))
- print(BinarySearch(list, 91))
▲图 3-16
请注意,如果在输入列表中找到了值,调用BinarySearch函数将返回True。
- 二分查找的性能:二分查找之所以如此命名,是因为在每次迭代中,算法都会将数据分成两部分。如果数据有N项,则它最多需要O(log N)步来完成迭代,这意味着算法的运行时间为O(log N)。
三. 插值查找
二分查找的基本逻辑是关注数据的中间部分。插值查找更加复杂,它使用目标值来估计元素在有序数组中的大概位置。
让我们试着用一个例子来理解它:假设我们想在一本英文词典中搜索一个单词,比如单词river,我们将利用这些信息进行插值,并开始查找以字母r开头的单词,而不是翻到字典的中间开始查找。一个更通用的插值查找程序如下所示:
- def IntPolsearch(list,x ):
- idx0 = 0
- idxn = (len(list) - 1)
- found = False
- while idx0 <= idxn and x >= list[idx0] and x <= list[idxn]:
- # Find the mid point
- mid = idx0 +int(((float(idxn - idx0)/( list[idxn] - list[idx0])) * ( x - list[idx0])))
- # Compare the value at mid point with search value
- if list[mid] == x:
- found = True
- return found
- if list[mid] < x:
- idx0 = mid + 1
- return found
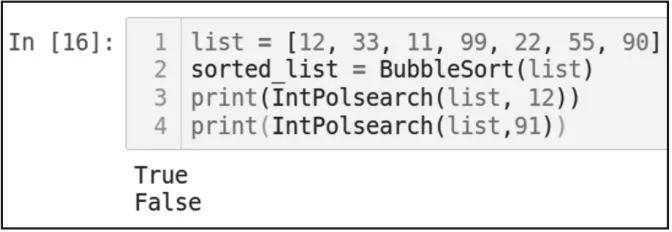
输出结果如图3-17所示。
- list = [12, 33, 11, 99, 22, 55, 90]
- sorted_list = BubbleSort(list)
- print(IntPolsearch(list, 12))
- print(IntPolsearch(list,91))
▲图 3-17
请注意,在使用IntPolsearch函数之前,首先需要使用排序算法对数组进行排序。
- 插值查找的性能:如果数据分布不均匀,则插值查找算法的性能会很差,该算法的最坏时间复杂度是O(N)。如果数据分布得相当均匀,则最佳时间复杂度是O(log(log N))。
关于作者:伊姆兰·艾哈迈德(Imran Ahmad) 是一名经过认证的谷歌讲师,多年来一直在谷歌和学习树(Learning Tree)任教,主要教授Python、机器学习、算法、大数据和深度学习。他在攻读博士学位期间基于线性规划方法提出了名为ATSRA的新算法,用于云计算环境中资源的优化分配。近4年来,他一直在加拿大联邦政府的高级分析实验室参与一个备受关注的机器学习项目。
本文摘编自《程序员必会的40种算法》,经出版方授权发布。