划分字母区间
字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。
示例:
- 输入:S = "ababcbacadefegdehijhklij"
- 输出:[9,7,8] 解释:划分结果为 "ababcbaca", "defegde", "hijhklij"。每个字母最多出现在一个片段中。像 "ababcbacadefegde", "hijhklij" 的划分是错误的,因为划分的片段数较少。
提示:
- S的长度在[1, 500]之间。
- S只包含小写字母 'a' 到 'z' 。
思路
一想到分割字符串就想到了回溯,但本题其实不用回溯去暴力搜索。
题目要求同一字母最多出现在一个片段中,那么如何把同一个字母的都圈在同一个区间里呢?
如果没有接触过这种题目的话,还挺有难度的。
在遍历的过程中相当于是要找每一个字母的边界,如果找到之前遍历过的所有字母的最远边界,说明这个边界就是分割点了。此时前面出现过所有字母,最远也就到这个边界了。
可以分为如下两步:
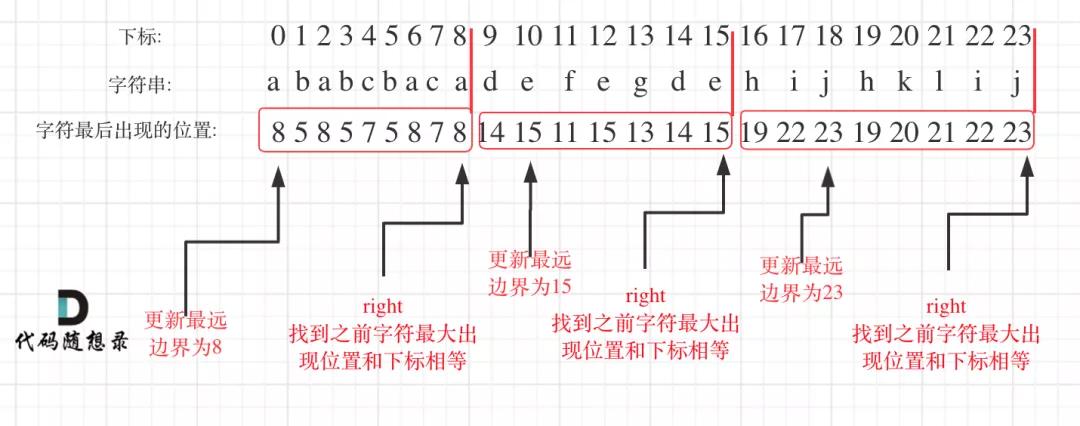
- 统计每一个字符最后出现的位置
- 从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点
如图:
划分字母区间
明白原理之后,代码并不复杂,如下:
- class Solution {
- public:
- vector<int> partitionLabels(string S) {
- int hash[27] = {0}; // i为字符,hash[i]为字符出现的最后位置
- for (int i = 0; i < S.size(); i++) { // 统计每一个字符最后出现的位置
- hash[S[i] - 'a'] = i;
- }
- vector<int> result;
- int left = 0;
- int right = 0;
- for (int i = 0; i < S.size(); i++) {
- right = max(right, hash[S[i] - 'a']); // 找到字符出现的最远边界
- if (i == right) {
- result.push_back(right - left + 1);
- left = i + 1;
- }
- }
- return result;
- }
- };
空间复杂度:O(1) 使用的hash数组是固定大小
总结
这道题目leetcode标记为贪心算法,说实话,我没有感受到贪心,找不出局部最优推出全局最优的过程。就是用最远出现距离模拟了圈字符的行为。
但这道题目的思路是很巧妙的,所以有必要介绍给大家做一做,感受一下。