二叉树中和为某一值的路径-判断是否为完全二叉树

Leetcode : https://leetcode-cn.com/problems/er-cha-shu-zhong-he-wei-mou-yi-zhi-de-lu-jing-lcof

“GitHub : https://gitee.com/nateshao/leetcode/blob/main/algo-notes/src/main/java/com/nateshao/sword_offer/topic_27_pathSum/Solution.java

二叉树中和为某一值的路径

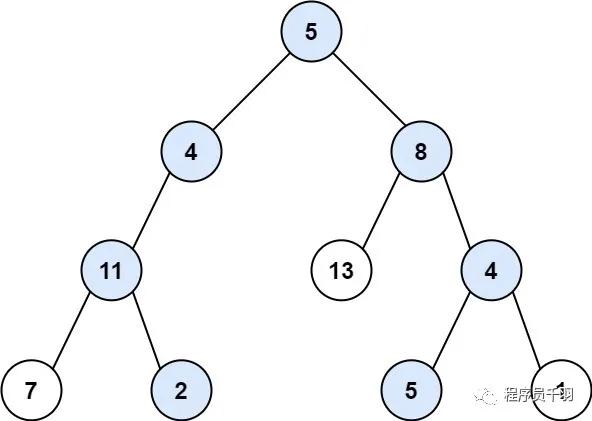
“题目描述：给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有从根节点到叶子节点路径总和等于给定目标和的路径。难度：中等叶子节点是指没有子节点的节点。示例 1：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 
 
输出：[[5,4,11,2],[5,8,4,5]] 
1.
2.
3.

示例 2：

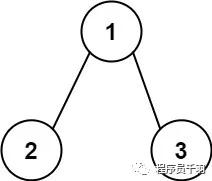
输入：root = [1,2,3], targetSum = 5 
 
输出：[] 
1.
2.
3.

示例 3：

输入：root = [1,2], targetSum = 0 
 
输出：[] 
1.
2.
3.

解题思路：

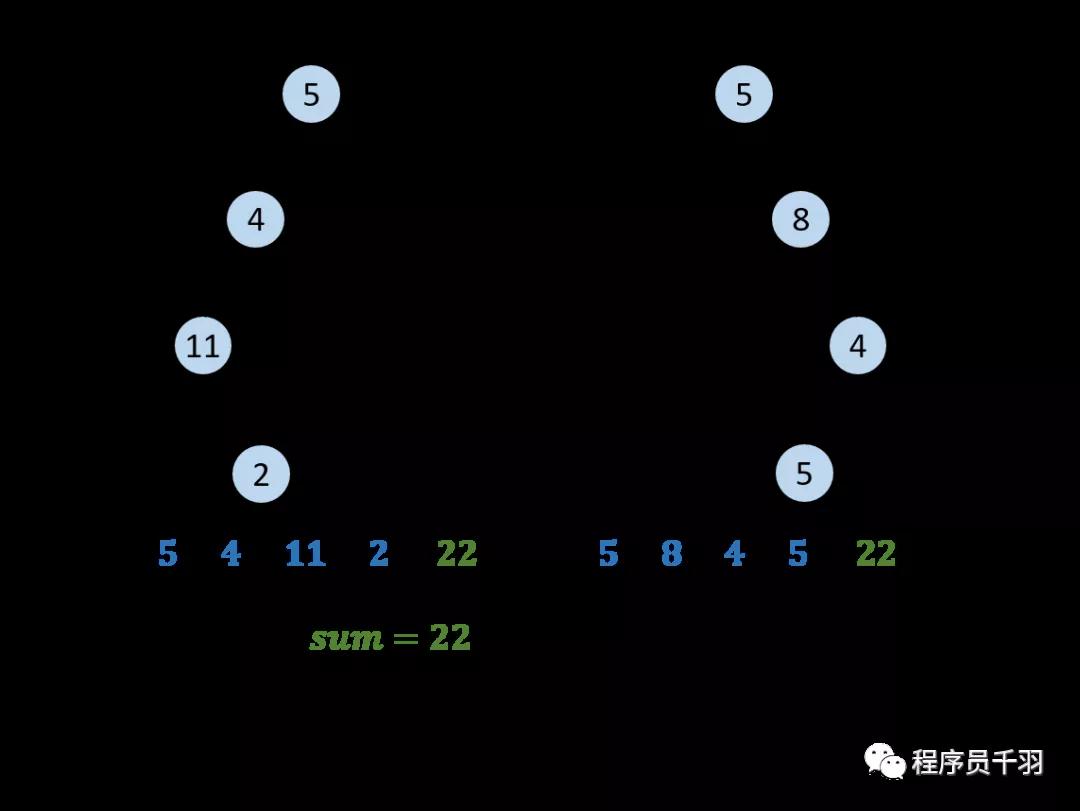
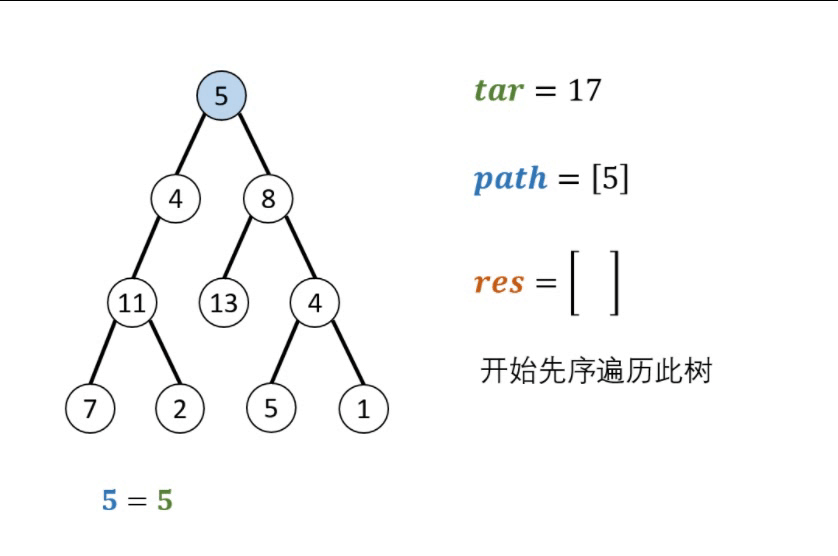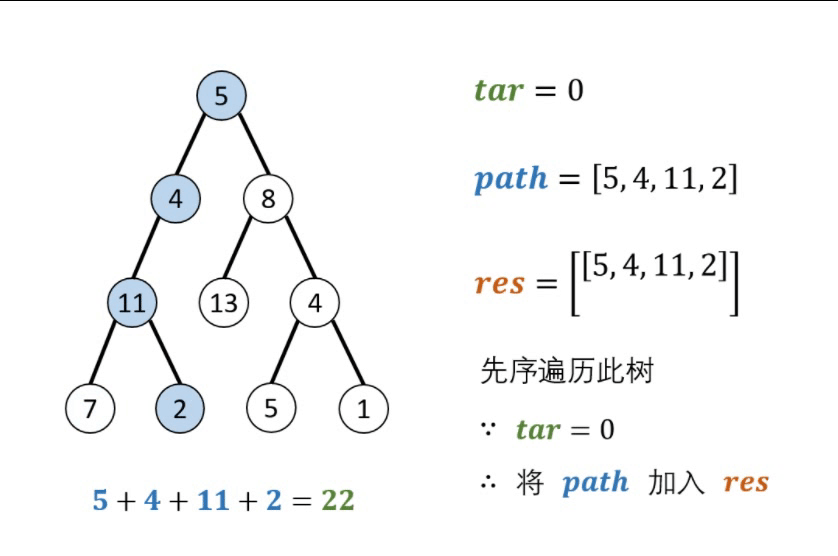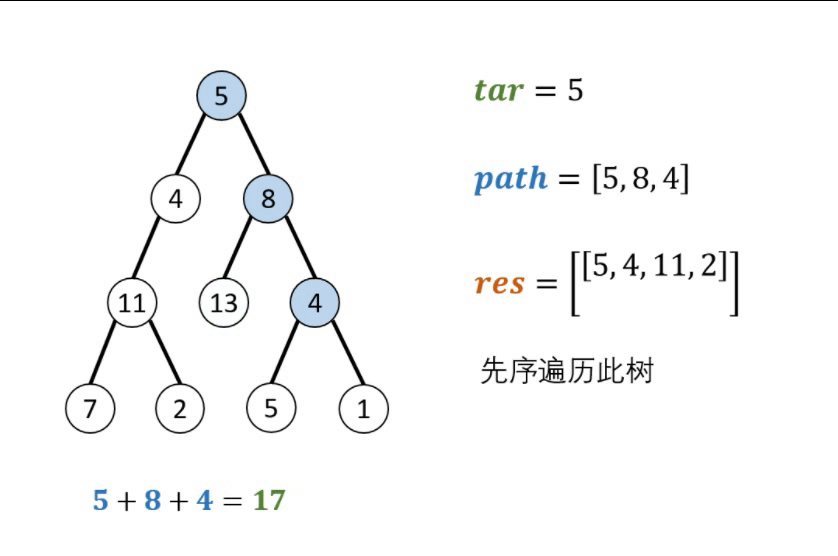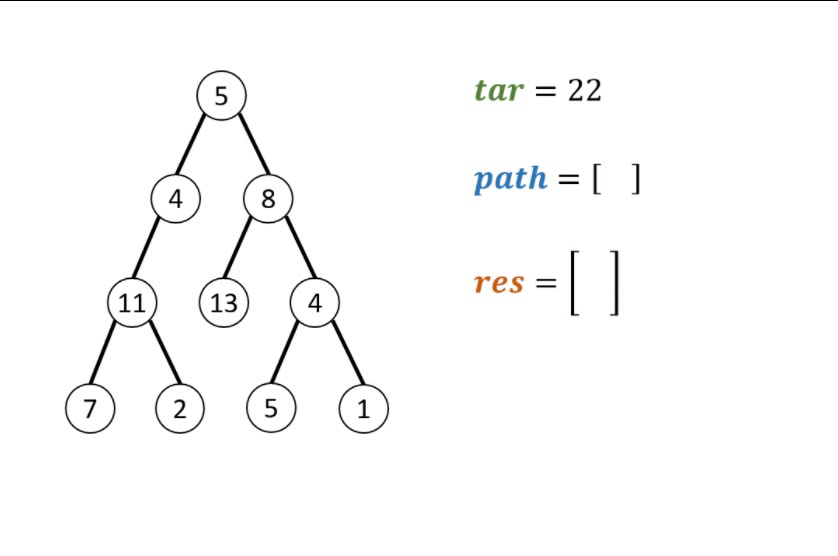
“本问题是典型的二叉树方案搜索问题，使用回溯法解决，其包含先序遍历 + 路径记录两部分。

先序遍历：按照 “根、左、右” 的顺序，遍历树的所有节点。
路径记录：在先序遍历中，记录从根节点到当前节点的路径。当路径为 ① 根节点到叶节点形成的路径且 ② 各节点值的和等于目标值 sum 时，将此路径加入结果列表。

算法流程：pathSum(root，sum) 函数:

初始化：结果列表res，路径列表 path.
返回值：返回res即可。

recur (root, tar) 函数:

递推参数：当前节点root，当前目标值tar 。
终止条件：若节点root为空，则直接返回。
递推工作：
- 路径更新：将当前节点值root. val加入路径path ;
- 目标值更新：tar=tar - root.val(即目标值tar从sum减至0);
- 路径记录：当①root为叶节点且②路径和等于目标值，则将此路径path加入res。
- 先序遍历：递归左1右子节点。
- 路径恢复：向上回溯前，需要将当前节点从路径path中删除，即执行path. pop()。

复杂度分析：

时间复杂度 O(N)： N 为二叉树的节点数，先序遍历需要遍历所有节点。
空间复杂度 O(N)：最差情况下，即树退化为链表时，path 存储所有树节点，使用 O(N) 额外空间。

package com.nateshao.sword_offer.topic_27_pathSum; 
 
import java.util.ArrayList; 
import java.util.LinkedList; 
import java.util.List; 
 
/** 
 * @date Created by 邵桐杰 on 2021/12/1 16:45 
 * @微信公众号 程序员千羽 
 * @个人网站 www.nateshao.cn 
 * @博客 https://nateshao.gitee.io 
 * @GitHub https://github.com/nateshao 
 * @Gitee https://gitee.com/nateshao 
 * Description: 二叉树中和为某一值的路径 
 */ 
public class Solution { 
 
    public static void main(String[] args) { 
        TreeNode node1 = new TreeNode(10); 
        TreeNode node2 = new TreeNode(5); 
        TreeNode node3 = new TreeNode(12); 
        TreeNode node4 = new TreeNode(4); 
        TreeNode node5 = new TreeNode(7); 
 
        node1.left = node2; 
        node1.right = node3; 
        node2.left = node4; 
        node2.right = node5; 
 
        Solution p = new Solution(); 
        System.out.println(p.listAll); 
        p.pathSum(node1, 22); 
        for (List<Integer> list : p.listAll) { 
            for (int i : list) { 
                System.out.print(i + " "); 
            } 
            System.out.println(); 
        } 
        /** 
         * [] 
         * 10 5 7 
         * 10 12 
         */ 
    } 
 
    /****************************** 剑指offer **********************************/ 
 
    private static List<List<Integer>> listAll = new ArrayList<>(); 
    private static List<Integer> list = new ArrayList<>(); 
 
    /** 
     * 思路：先保存根节点，然后分别递归在左右子树中找目标值，若找到即到达叶子节点，打印路径中的值 
     * 
     * @param root 
     * @param target 
     * @return 
     */ 
    public static List<List<Integer>> pathSum(TreeNode root, int target) { 
        if (root == null) return listAll; 
        list.add(root.val); 
        target -= root.val; 
        if (target == 0 && root.left == null && root.right == null) { 
            listAll.add(new ArrayList<>(list)); 
        } 
        pathSum(root.left, target); 
        pathSum(root.right, target); 
        list.remove(list.size() - 1); 
        return listAll; 
    } 
 
 
    /*********************** 精选解答 ***************************/ 
    LinkedList<List<Integer>> res = new LinkedList<>(); 
    LinkedList<Integer> path = new LinkedList<>(); 
 
    public List<List<Integer>> pathSum2(TreeNode root, int sum) { 
        recur(root, sum); 
        return res; 
    } 
 
    void recur(TreeNode root, int tar) { 
        if (root == null) return; 
        path.add(root.val); 
        tar -= root.val; 
        if (tar == 0 && root.left == null && root.right == null) 
            res.add(new LinkedList(path)); 
        recur(root.left, tar); 
        recur(root.right, tar); 
        path.removeLast(); 
    } 
 
 
    public static class TreeNode { 
        int val; 
        TreeNode left; 
        TreeNode right; 
 
        TreeNode() { 
        } 
 
        TreeNode(int val) { 
            this.val = val; 
        } 
 
        TreeNode(int val, TreeNode left, TreeNode right) { 
            this.val = val; 
            this.left = left; 
            this.right = right; 
        } 
    } 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
101.
102.
103.
104.
105.
106.
107.
108.
109.
110.
111.