动画：Interpolator插值器使用和自定义详解

[[438230]]

前言

属性动画可以对某个属性做动画，而插值器(TimeInterpolator)和估值器(TypeEvaluator)在其中扮演了重要角色;

那么今天我们了解下 插值器TimeInterpolator;

一、插值器介绍

1、Interpolator有什么用

• Interpolator 被用来修饰动画效果，定义动画的变化率;
• 在Android源码中对应的接口类为TimeInterpolator，通过输入均匀变化的0~1之间的值;
• 可以得到匀速、正加速、负加速、无规则变加速等0~1之间的变化曲线;

2、应用场景

• 实现非线性运动的动画效果;
• 非线性运动是指动画改变的速率不是一成不变的，如加速、减速运动的动画效果;
• 实现复杂的曲线动画，回弹效果自定义等都需要自定义插值器;

3、Android系统提供的插值器类型

• AccelerateDecelerateInterpolator 在动画开始与结束比较慢，中间加速
• AccelerateInterpolator 加速
• AnticipateInterpolator 开始的时候向后然后向前甩
• AnticipateOvershootInterpolator 开始的时候向后然后向前甩一定值后返回最后的值
• BounceInterpolator 动画结束的时候弹起
• CycleInterpolator 动画循环播放特定的次数，速率改变沿着正弦曲线
• DecelerateInterpolator 减速
• LinearInterpolator 以常量速率改变
• OvershootInterpolator 向前甩一定值后再回到原来位置

二、插值器应用

插值器的使用有两种方式：在XML和代码中使用

1、xml

XML动画文件使用插值器时，需要设置系统设置的对应的插值器资源ID

<?xml version="1.0" encoding="utf-8"?> 
<set xmlns:android="http://schemas.android.com/apk/res/android"> 
    <alpha 
        android:fromAlpha="1.0" 
        android:toAlpha="0.1" 
        android:duration="2000" 
        android:repeatMode="reverse" 
        android:repeatCount="infinite" 
        android:interpolator="@android:anim/linear_interpolator"/> 
</set> 

2、代码中使用

• 代码使用插值器时，只需创建对应的插值器对象，然后设置给动画对象;也可以加载xml文件中配置的插值器;
• 利用view的setInterpolator(Context context, @AnimRes @InterpolatorRes int resID)设置插值器;

//创建一个渐变透明度的动画，从透明到完全不透明 
AlphaAnimation alphaAnimation = new AlphaAnimation(0.1f, 1.0f); 
//设置动画时长 
alphaAnimation.setDuration(5000); 
//设置动画重复方式 
alphaAnimation.setRepeatMode(AlphaAnimation.REVERSE); 
//设置动画播放次数 
alphaAnimation.setRepeatCount(AlphaAnimation.INFINITE); 
//设置匀速插值器 
alphaAnimation.setInterpolator(new LinearInterpolator()); 
//为View开启指定类型动画 
imageView.startAnimation(alphaAnimation) 

• 使用Android内置的插值器能满足大多数的动画需求;
• 如果系统提供的插值器无法满足需求，还可以自定义插值器;

三、自定义插值器

1、实现方式

• 自定义插值器需要实现Interpolator或TimeInterpolator接口，并复写getInterpolation()方法;
• 补间动画 实现 Interpolator接口;属性动画实现TimeInterpolator接口;
• TimeInterpolator接口是属性动画中新增的，用于兼容Interpolator接口，这使得所有过去的Interpolator实现类都可以直接在属性动画使用;

Interpolator接口和TimeInterpolator接口说明如下：

// Interpolator接口 
public interface Interpolator {   
    // 内部只有一个方法：getInterpolation() 
     float getInterpolation(float input) {   
        // 参数说明 
        // input值值变化范围是0-1，且随着动画进度（0% - 100% ）均匀变化 
        // 即动画开始时，input值 = 0；动画结束时input = 1 
        // 而中间的值则是随着动画的进度（0% - 100%）在0到1之间均匀增加 
      ...// 插值器的计算逻辑 
      return xxx； 
      // 返回的值就是用于估值器继续计算的fraction值，下面会详细说明 
    }   
// TimeInterpolator接口 
public interface TimeInterpolator {   
    float getInterpolation(float input){ 
// input值值变化范围是0-1，且随着动画进度（0% - 100% ）均匀变化 
      ...// 插值器的计算逻辑 
    };   
}   

自定义插值器的关键在于：对input值根据动画的进度(0%-100%)通过逻辑计算从而计算出当前属性值改变的百分比;

2、自定义插值器

写一个自定义Interpolator：先减速后加速

/* 
 * 根据需求实现Interpolator接口 
 * TestInterpolator.java 
 */ 
public class TestInterpolator implements TimeInterpolator { 
    @Override 
    public float getInterpolation(float input) { 
        float result; 
        if (input <= 0.5) { 
            result = (float) (Math.sin(Math.PI * input)) / 2; 
            // 使用正弦函数来实现先减速后加速的功能，逻辑如下： 
            // 因为正弦函数初始弧度变化值非常大，刚好和余弦函数是相反的 
            // 随着弧度的增加，正弦函数的变化值也会逐渐变小，这样也就实现了减速的效果。 
            // 当弧度大于π/2之后，整个过程相反了过来，现在正弦函数的弧度变化值非常小，渐渐随着弧度继续增加，变化值越来越大，弧度到π时结束，这样从0过度到π，也就实现了先减速后加速的效果 
        } else { 
            result = (float) (2 - Math.sin(Math.PI * input)) / 2; 
        } 
        return result; 
        // 返回的result值 = 随着动画进度呈先减速后加速的变化趋势 
    } 
} 
/* 
 * 步骤设置使用 
 * Test.java 
 */ 
 //  创建动画作用对象：此处以Button为例 
 mButton = (Button) findViewById(R.id.Button); 
 //  获得当前按钮的位置 
float curTranslationX = mButton.getTranslationX(); 
//  创建动画对象 & 设置动画 
ObjectAnimator animator = ObjectAnimator.ofFloat(mButton, "translationX", curTranslationX, 300,curTranslationX); 
// 表示的是: 
// 动画作用对象是mButton 
// 动画作用的对象的属性是X轴平移 
// 动画效果是:从当前位置平移到 x=1500 再平移到初始位置 
//  设置步骤1中设置好的插值器：先减速后加速 
animator.setInterpolator(new TestInterpolator()); 
// 启动动画 
animator.start(); 

3、贝塞尔曲线的插值器

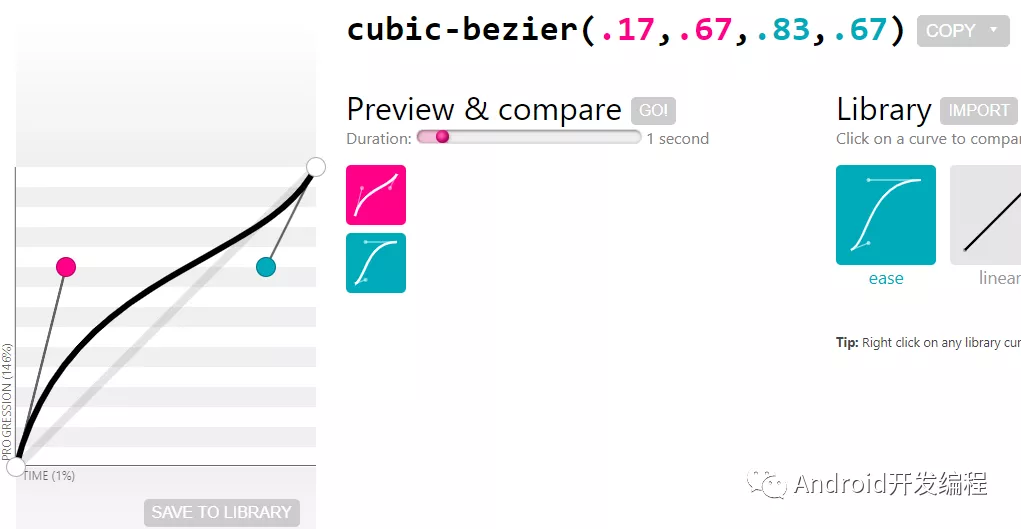
(1)先使用贝塞尔曲线数值生成工具来获取想要的曲线数值

• 工具网站：https://cubic-bezier.com/;
• 拉拽左边图像的2个点，调整出符合效果的图形;
• 点击Go按键，可看到红色与蓝色的方块运动状态，调节自己想要的效果;
• 将4个参数运用到下面的代码中;

(2)代码运用

ObjectAnimator animator = ObjectAnimator.ofFloat(mButton, "translationX", curTranslationX, 300,curTranslationX); 
EaseCubicInterpolator interpolator = new EaseCubicInterpolator(0.31f, 0.85f,0.77f, 0.14f); 
animator.setInterpolator(interpolator) 

(3)贝塞尔曲线插值器

import android.graphics.PointF; 
import android.view.animation.Interpolator; 
/** 
 * 缓动三次方曲线插值器.(基于三次方贝塞尔曲线) 
 */ 
public class EaseCubicInterpolator implements Interpolator { 
    private final static int ACCURACY = 4096; 
    private int mLastI = 0; 
    private final PointF mControlPoint1 = new PointF(); 
    private final PointF mControlPoint2 = new PointF(); 
    /** 
     * 设置中间两个控制点 
     * 
     * 在线工具: http://cubic-bezier.com 
     * 
     * @param x1 
     * @param y1 
     * @param x2 
     * @param y2 
     */ 
    public EaseCubicInterpolator(float x1, float y1, float x2, float y2) { 
        mControlPoint1.x = x1; 
        mControlPoint1.y = y1; 
        mControlPoint2.x = x2; 
        mControlPoint2.y = y2; 
    } 
    @Override 
    public float getInterpolation(float input) { 
        float t = input; 
        // 近似求解t的值[0,1] 
        for (int i = mLastI; i < ACCURACY; i++) { 
            t = 1.0f * i / ACCURACY; 
            double x = cubicCurves(t, 0, mControlPoint1.x, mControlPoint2.x, 1); 
            if (x >= input) { 
                mLastI = i; 
                break; 
            } 
        } 
        double value = cubicCurves(t, 0, mControlPoint1.y, mControlPoint2.y, 1); 
        if (value > 0.999d) { 
            value = 1; 
            mLastI = 0; 
        } 
        return (float) value; 
    } 
    /** 
     * 求三次贝塞尔曲线(四个控制点)一个点某个维度的值.<br> 
     * <p> 
     * 
     * @param t      取值[0, 1] 
     * @param value0 
     * @param value1 
     * @param value2 
     * @param value3 
     * @return 
     */ 
    public static double cubicCurves(double t, double value0, double value1, 
                                     double value2, double value3) { 
        double value; 
        double u = 1 - t; 
        double tt = t * t; 
        double uu = u * u; 
        double uuu = uu * u; 
        double ttt = tt * t; 
        value = uuu * value0; 
        value += 3 * uu * t * value1; 
        value += 3 * u * tt * value2; 
        value += ttt * value3; 
        return value; 
    } 
} 

总结

要实现复杂的动画效果时，就要自定义插值器，其实插值器还是的学习算法;

大家一起加油;