一篇学会包含 Min 函数的栈-包含min函数的栈 python

本文转载自微信公众号「程序员千羽」，作者程序员千羽。转载本文请联系程序员千羽公众号。

Leetcode : https://leetcode-cn.com/problems/bao-han-minhan-shu-de-zhan-lcof

“GitHub : https://gitee.com/nateshao/leetcode/blob/main/algo-notes/src/main/java/com/nateshao/sword_offer/topic_23_MinStack/MinStack.java

包含min函数的栈

“题目描述：定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中，调用 min、push 及 pop 的时间复杂度都是 O(1)。示例：

MinStack minStack = new MinStack(); 
minStack.push(-2); 
minStack.push(0); 
minStack.push(-3); 
minStack.min();   --> 返回 -3. 
minStack.pop(); 
minStack.top();   --> 返回 0. 
minStack.min();   --> 返回 -2.

提示：

各函数的调用总次数不超过 20000 次

解题思路：定义两个栈，一个存放入的值。另一个存最小值。

“普通栈的 push() 和 pop() 函数的复杂度为 O(1) ;而获取栈最小值 min() 函数需要遍历整个栈，复杂度为 O(N) 。

本题难点:将min() 函数复杂度降为0(1)，可通过建立辅助栈实现;
- 数据栈A：栈A用于存储所有元素，保证入栈push() 函数、出栈pop() 函数、获取栈顶top()函数的正常逻辑。
- 辅助栈B：栈B中存储栈A中所有非严格降序的元素，则栈A中的最小元素始终对应栈B的栈顶元素，即min() 函数只需返回栈B的栈顶元素即可。

因此,只需设法维护好栈B的元素，使其保持非严格降序,即可实现min() 函数的0(1)复杂度。

函数设计：

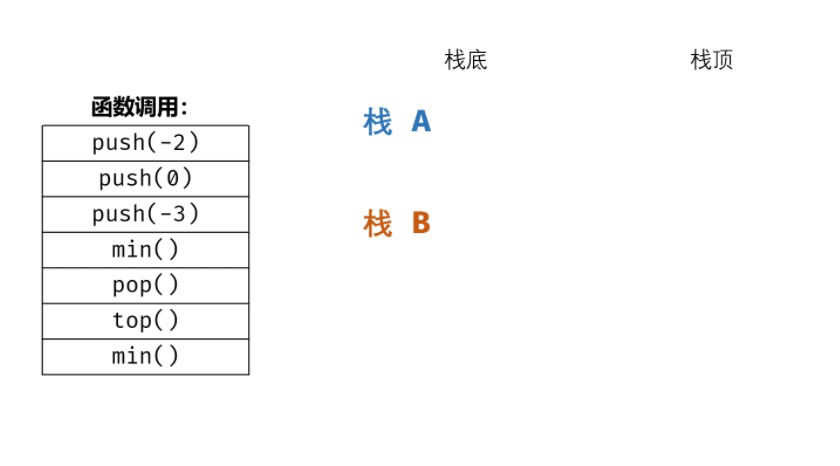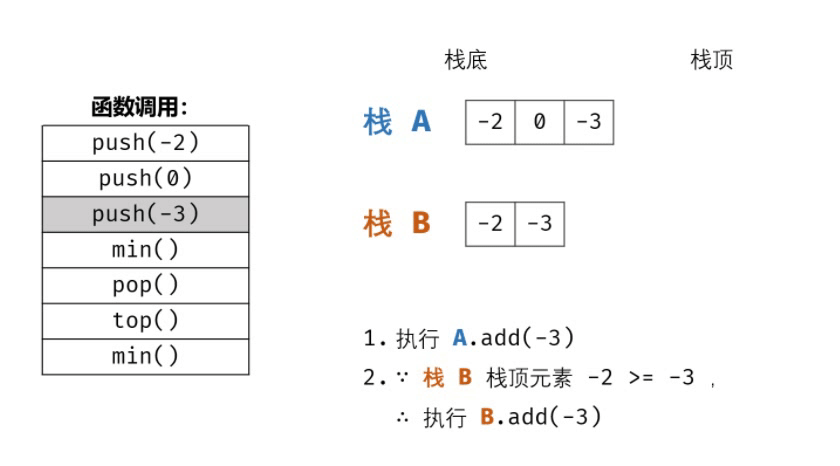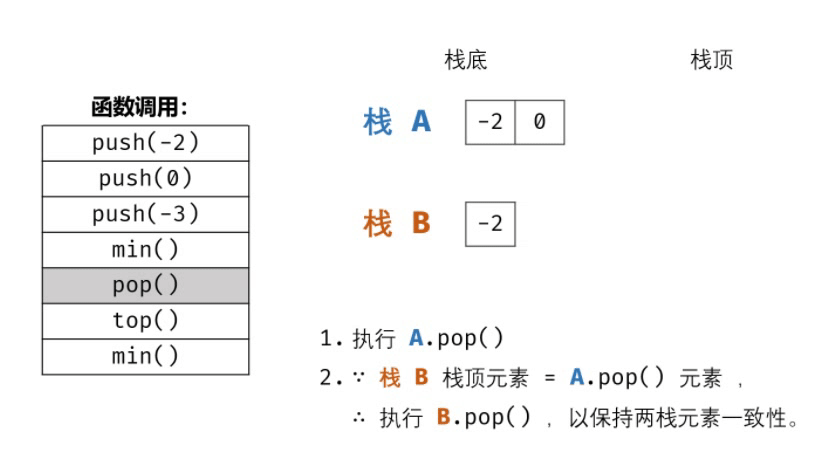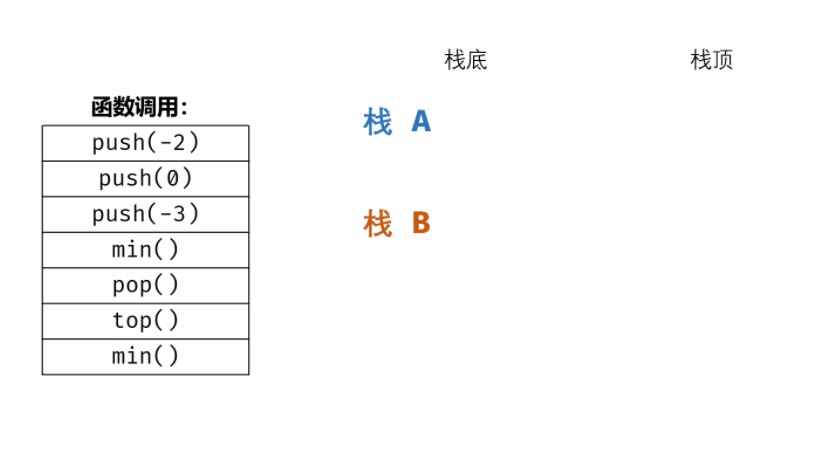
push(x) 函数：重点为保持栈 B 的元素是非严格降序的。
- 将 x 压入栈 A(即 A.add(x) );
- 若 ① 栈 B 为空或 ② x 小于等于栈 B 的栈顶元素，则将 x 压入栈 B (即 B.add(x) )。
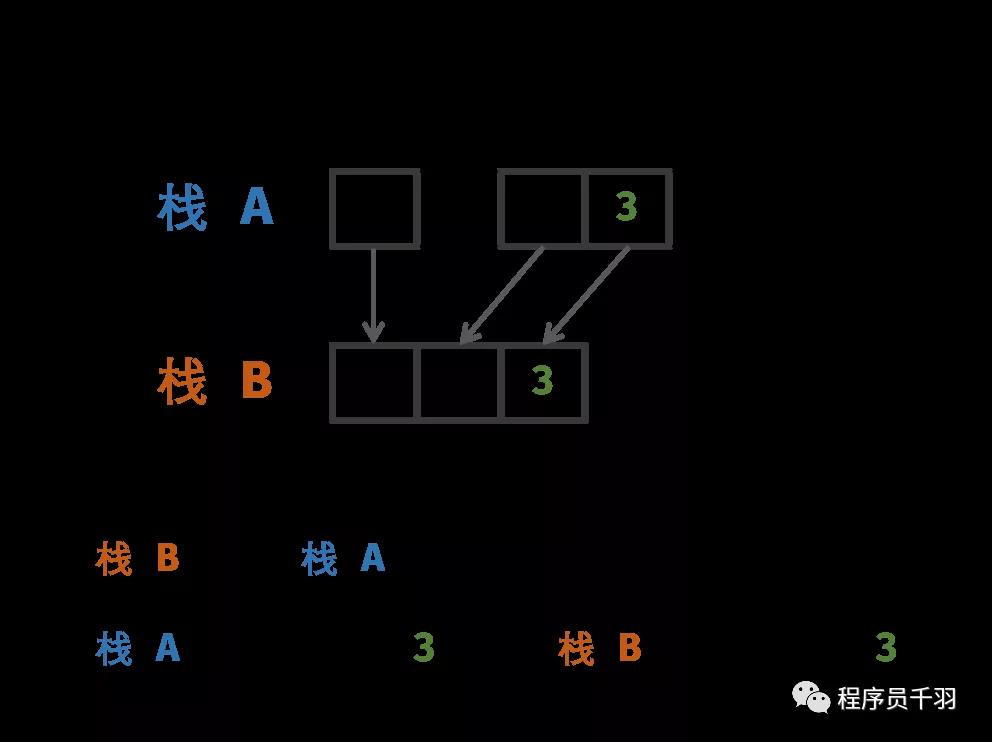
pop() 函数：重点为保持栈 A, B 的元素一致性。
- 执行栈 A 出栈(即 A.pop() )，将出栈元素记为 y ;
- 若 y 等于栈 B 的栈顶元素，则执行栈 B 出栈(即 B.pop() )。
top() 函数：直接返回栈 A 的栈顶元素即可，即返回 A.peek() 。
min() 函数：直接返回栈 B 的栈顶元素即可，即返回 B.peek() 。

复杂度分析：

时间复杂度 O(1) ： push(), pop(), top(), min() 四个函数的时间复杂度均为常数级别。
空间复杂度 O(N) ：当共有 N个待入栈元素时，辅助栈 B最差情况下存储 N 个元素，使用 O(N)额外空间。

“Java 代码中，由于 Stack 中存储的是 int 的包装类 Integer ，因此需要使用 equals() 代替 == 来比较值是否相等。此题如果用==将会无法通过 Integer的equals重写过，比较的是内部value的值， ==如果在[-128,127]会被cache缓存,超过这个范围则比较的是对象是否相同

package com.nateshao.sword_offer.topic_23_MinStack; 
 
import java.util.Stack; 
 
/** 
 * @date Created by 邵桐杰 on 2021/11/28 21:38 
 * @微信公众号 程序员千羽 
 * @个人网站 www.nateshao.cn 
 * @博客 https://nateshao.gitee.io 
 * @GitHub https://github.com/nateshao 
 * @Gitee https://gitee.com/nateshao 
 * Description: 包含min函数的栈 
 * 思路：定义两个栈，一个存放入的值。另一个存最小值。 
 */ 
public class MinStack { 
    private Stack<Integer> stack1; // 数据栈 
    private Stack<Integer> stack2; // 辅助栈，记录每次有元素进栈后或者出栈后，元素的最小值 
 
    /** 
     * initialize your data structure here. 
     */ 
    public MinStack() { 
        // 初始化辅助栈和数据栈 
        stack1 = new Stack<>(); 
        stack2 = new Stack<>(); 
    } 
 
    public void push(int x) { 
        // 数据栈，进栈 
        stack1.push(x); 
        // 如果记录当前数据栈中最小值的辅助栈为空，或者最小值小于 x，则将 x 设置为最小值，即进辅助栈 
        if (stack2.isEmpty() || stack2.peek() >= x) stack2.push(x); 
    } 
 
    public void pop() { 
        if (stack1.pop().equals(stack2.peek())) stack2.pop(); 
    } 
 
    public int top() { 
        return stack1.peek(); 
    } 
 
    public int min() { 
        return stack2.peek(); 
    } 
 
    /** 
     * Your MinStack object will be instantiated and called as such: 
     * MinStack obj = new MinStack(); 
     * obj.push(x); 
     * obj.pop(); 
     * int param_3 = obj.top(); 
     * int param_4 = obj.min(); 
     */ 
 
    /** 
     * 精选解答 
     */ 
    class MinStack1 { 
 
        Stack<Integer> A, B; 
 
        public MinStack1() { 
            A = new Stack<>(); 
            B = new Stack<>(); 
        } 
 
        public void push(int x) { 
            A.add(x); 
            if (B.empty() || B.peek() >= x) 
                B.add(x); 
        } 
 
        public void pop() { 
            if (A.pop().equals(B.peek())) 
                B.pop(); 
        } 
 
        public int top() { 
            return A.peek(); 
        } 
 
        public int min() { 
            return B.peek(); 
        } 
    } 
}

参考链接：https://leetcode-cn.com/problems/bao-han-minhan-shu-de-zhan-lcof/solution