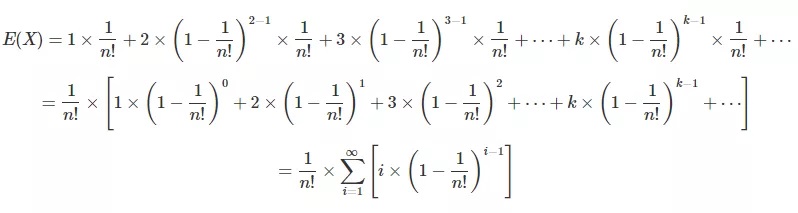今天,和大家分享一个,世界上最慢的排序算法,猴子排序(bogo sort)。
话不多说,先上伪代码:
int bogo_sort(int& arr[], int n){
while(false== is_sorted(arr[n])){
random_shuffle(arr[n]);
}
return 0;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
之所以叫猴子排序,源自典故:一只猴子随机敲击键盘,只要时间足够久,一定能敲出莎士比亚的诗。
看了伪代码,很容易理解其核心思路是:
(1)判断待排序的数组是否有序,有序则返回排序完毕;
(2)无序,则随机打乱数组;
(3)重复(1);
只要执行的时间足够长,随机的次数足够久,总能够得到排序后的结果,它号称是世界上最慢的排序算法。
那么问题来了,这个排序有什么用呢?
我能够想到的,就是大学里作为算法课的时间复杂度推导习题,或者面试过程中时间复杂度计算考题了,又或者装13的谈资了,其他好像没有什么用。
那这个排序算法的时间复杂度是多少呢?
简单来分析一下。
n个元素随机打乱,有n!种组合。
- 一次排序成功的概率是p1 = 1/n!,一次排序失败的概率是p2 = 1-p1;
- 两次排序成功的概率是p2*p1;画外音:第1次失败,第2次成功。
- 三次排序成功的概率是p2^2*p1;画外音:前2次失败,第3次成功。
- …
- k次排序成功的概率是p2^(k-1)*p1画外音:前k-1次失败,第k次成功。
- …
于是,平均排序成功次数的期望:
E(X) =1次 * 一次成功的概率+2次 * 二次成功的概率+3次 * 三次成功的概率+…+k次 * k次成功的概率+…
即:
最后,根据大家大学里学的无穷级数的数学知识,“很容易”得到,其时间复杂度是O(n*n!),这是一个阶乘级别的算法。
【本文为51CTO专栏作者“58沈剑”原创稿件,转载请联系原作者】