聊聊判断二叉树A中是否包含子树B-b+树二叉树

Leetcode : https://leetcode-cn.com/problems/shu-de-zi-jie-gou-lcof

“GitHub : https://github.com/nateshao/leetcode/blob/main/algo-notes/src/main/java/com/nateshao/sword_offer/topic_20_isSubStructure/Solution.java

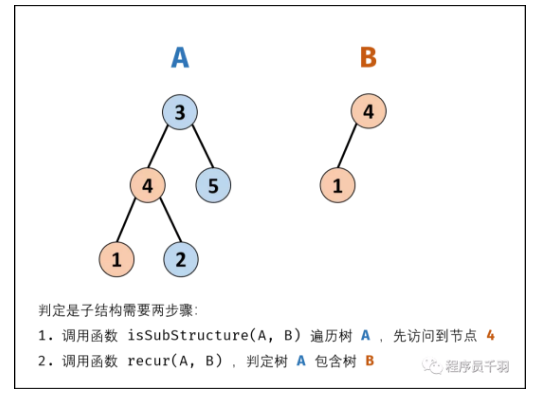
判断二叉树A中是否包含子树B

“题目描述：输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)B是A的子结构，即 A中有出现和B相同的结构和节点值。例如：给定的树 A：

给定的树 B：

返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。示例 1：

输入：A = [1,2,3], B = [3,1] 
 
输出：false

示例 2：

输入：A = [3,4,5,1,2], B = [4,1] 
 
输出：true

限制：0 <= 节点个数 <= 10000

解题思路:若树B是树A的子结构,则子结构的根节点可能为树A的任意一个节点。因此,判断树B是否是树A的子结构，需完成以下两步工作:

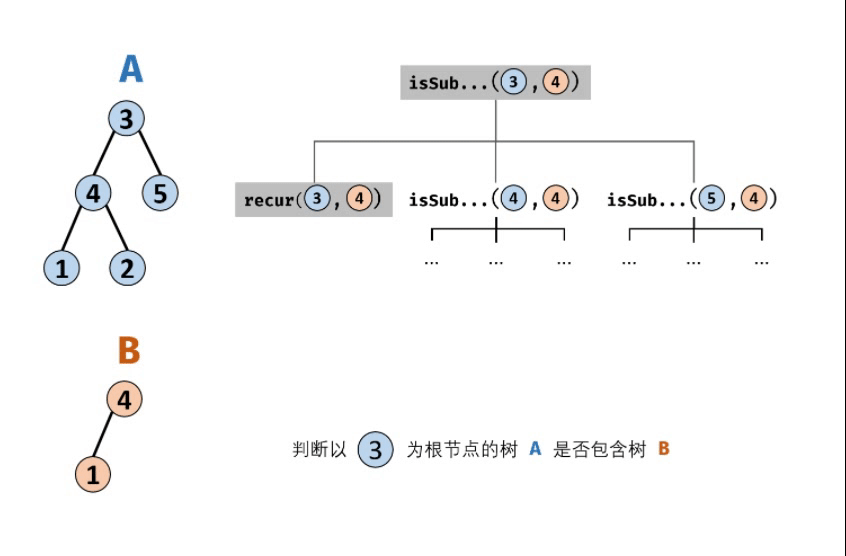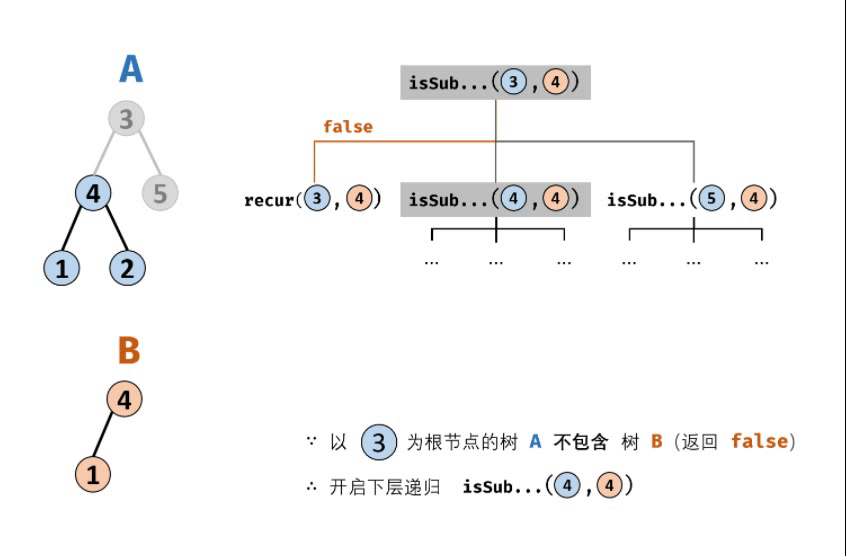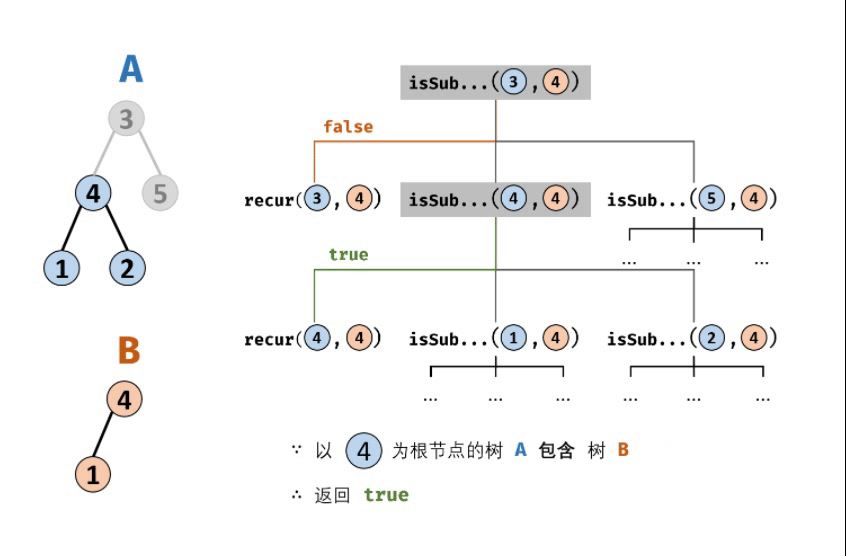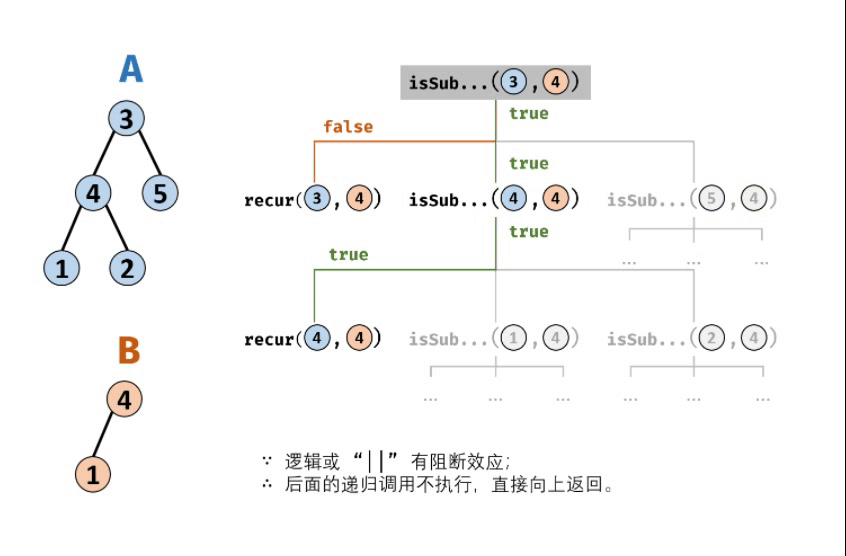
先序遍历树A中的每个节点nA ; (对应函数 isSubStructure(A, B) )

判断树A中以nA为根节点的子树否包含树B。(对应函数recur(A,B))

算法流程：

“名词规定：树 A 的根节点记作节点 A ，树 B 的根节点称为节点 B 。

recur(A, B) 函数：

1.终止条件：

当节点 B为空：说明树 B 已匹配完成(越过叶子节点)，因此返回 true ;
当节点 A为空：说明已经越过树 A 叶子节点，即匹配失败，返回 false ;
当节点 A 和 B 的值不同：说明匹配失败，返回 false ;

2.返回值：

判断A和B的左子节点是否相等，即recur(A. left, B. left) ;
判断A和B的右子节点是否相等,即recur(A. right，B. right) ;

isSubStructure(A, B)函数:

特例处理：当树A为空或树B为空时，直接返回false;
返回值：若树B是树A的子结构,则必满足以下三种情况之一,因此用或|连接;
- 以节点A为根节点的子树包含树B，对应recur(A,B);
- 树B是树A左子树的子结构,对应isSubStructure(A. left， B) ;
- 树B是树A右子树的子结构，对应isSubStructure(A. right, B) ;

以让 2. 3.实质上是在对树A做先序遍历。

复杂度分析:

时间复杂度O(MN)：中M,N分别为树A和树B的节点数量;先序遍历树A占用0(M),每次调用recur(A, B)判断占用O(N)。
空间复杂度O(M)：
- 当树A和树B都退化为链表时，递归调用深度最大。
- 当M≤N时，遍历树A与递归判断的总递归深度为M ;
- 当M> N时，最差情况为遍历至树A叶子节点，此时总递归深度为M。

package com.nateshao.sword_offer.topic_20_isSubStructure; 
 
/** 
 * @date Created by 邵桐杰 on 2021/11/23 19:19 
 * @微信公众号 程序员千羽 
 * @个人网站 www.nateshao.cn 
 * @博客 https://nateshao.gitee.io 
 * @GitHub https://github.com/nateshao 
 * @Gitee https://gitee.com/nateshao 
 * Description: 判断二叉树A中是否包含子树B 
 */ 
class Solution { 
 
    /** 
     * 精选解答 
     * @param A 
     * @param B 
     * @return 
     */ 
    public static boolean isSubStructure1(TreeNode A, TreeNode B) { 
        return (A != null && B != null) && (recur1(A, B) || isSubStructure1(A.left, B) || isSubStructure1(A.right, B)); 
    } 
 
    public static boolean recur1(TreeNode A, TreeNode B) { 
        if (B == null) return true; 
        if (A == null || A.val != B.val) return false; 
        return recur1(A.left, B.left) && recur1(A.right, B.right); 
    } 
     
    /*********************************** 法二 *********************************************/ 
    //遍历A的每一个节点 
    public boolean isSubStructure(TreeNode A, TreeNode B) { 
        if (A == null || B == null) return false;//约定空树不是任意一个树的子结构 
        return recur(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B); 
    } 
 
    //同时遍历A和B的相同位置节点 
    boolean recur(TreeNode A, TreeNode B) { 
        //当B某个节点为null，则无需比较了，直接返回true，比较其他节点 
        if (B == null) return true; 
        //如果相同位置的两个节点不相同，则返回false，不用再继续比较了 
        if (A == null || A.val != B.val) return false; 
        //继续往下遍历比较 
        return recur(A.left, B.left) && recur(A.right, B.right); 
    } 
 
    public class TreeNode { 
        int val; 
        TreeNode left; 
        TreeNode right; 
 
        TreeNode(int x) { 
            val = x; 
        } 
    } 
}

参考链接：https://leetcode-cn.com/problems/shu-de-zi-jie-gou-lcof/solution/mian-shi-ti-26-shu-de-zi-jie-gou-xian-xu-bian-li-p