跳表这一数据结构,已经成为了Redis面试的高频考点。前两年没这么卷的时候,可能大家从开始学习,到拿到大厂offer这一过程,都可能没听说过跳表这一数据结构。
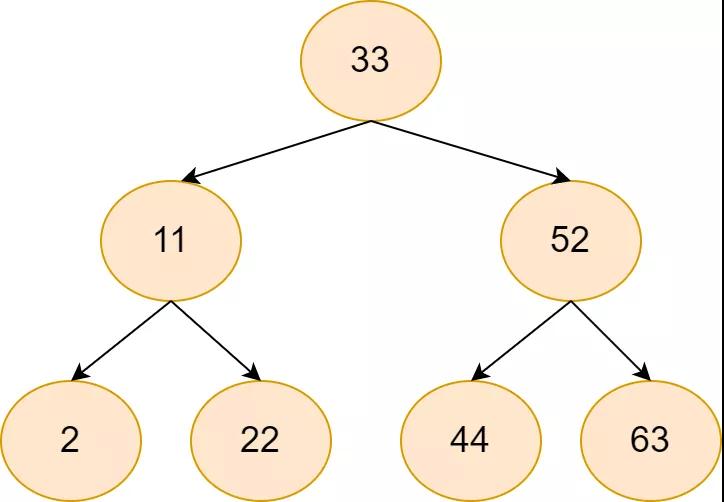
那什么是跳表呢?它是用来干啥的?AVL树红黑树知道吧,对,跳表跟他干的事情差不多。我举个例子大家就明白了。假设目前有一个有序数列:
- [2, 11,22, 33, 44, 52, 63]
我们想基于单链表的思想,设计一个数据结构,实现查找时间复杂度为O(logn)。单链表的话,它的结构长这个样子。
跳表1
当然这个结构,查找时间复杂度妥妥的O(n),那咋改呢?
那换个问法:一般做算法题,手撕代码面试的时候,当咱写了个时间复杂度为O(n)的解法,面试官摇摇头,问你有没有更好的方法,你会怎么做?
常见复杂度O(nlogn) O(n) O(logn) O(1),要优化,一步步来的话,只能上O(logn)了,那复杂度logn最常见的算法是哪个?当然是二分!
思路对了,那对着链表,咋把二分思想融合进去呢?
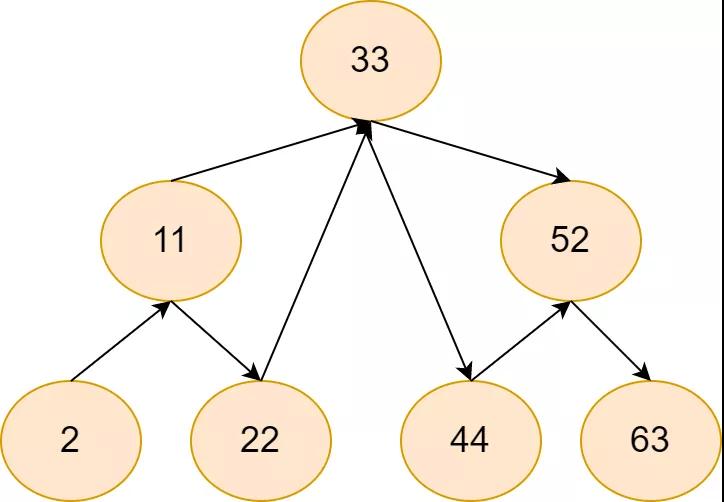
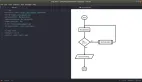
要不单链表指针这边动动刀子?让指针除了指向后面元素,还能越过几个节点,指向更后面元素?类似二叉查找树?先来看看这个数组对应的二叉查找树长什么样。
跳表2
当然,由于我们的结构是单链表,所以只能有由小值,指向大值,这个二叉树得改改。
跳表2
好像有点意思在里面了,再把原先单链表的性质加上。
跳表2
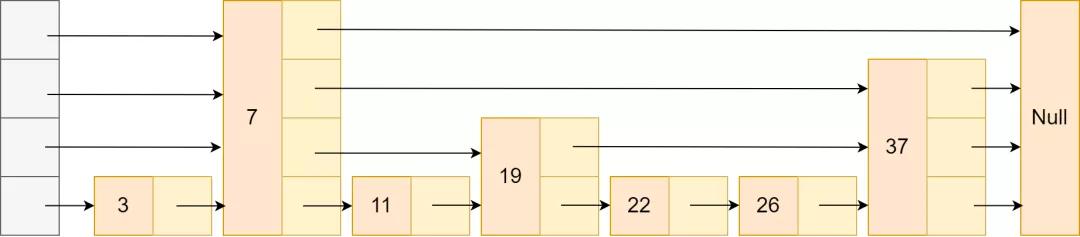
走线有点凌乱,按单链表的布局显示方式改改:(值得注意的是,我们需要新建一个数组项,每个数组项存储一个指针,指向刚刚二叉搜索树每一层最左侧的节点)
(咋感觉越看越像B+树了(雾))
来看个查找逻辑吧:
当查找到的结点保存的数,比要查找的数小时,跳表就会继续访问该层上的下一个结点。
当不满足时,跳表就会用到当前查找到的结点的指针数组的下一层指针,然后沿着下一层指针继续查找。
对于这种数据结构,我们需要从上往下依次查询三个链表,比如我们想查大于35的数字。
首先按左侧数组第一个找,发现中间节点是33,比较一下比35小。
发现33比35小,跳下一个节点。
发现该节点是Null,跳33的下一层节点。
发现52比35大,再跳下一层节点。
发现44比35大,跳下一层节点,但由于这是最后一层节点,即44是第一个比33大的数,满足最终条件,就找到了第一个比35大的数字。
我们知道,二叉平衡树,如果设计插入操作,会特别特别麻烦。对于由二叉平衡树思想改的跳表也是如此,对于我们这边的情况,每增加,或者减少一个新节点,每个节点的高度都需要变化。。那有没有高人改进呢?
既然把二叉平衡树改成这四不像了,为啥再不改改,能不能让他不平衡的同时,还能保证查找效率?
说实话,还真可以,来看看这种跳表。
跳表1
虽然这个跳表跟咱刚刚讲的跳表比起来,奇形怪状的,但按刚刚的查找思路,还是能做比较好的查询工作的。
而且既然表都长这么奇形怪状了,那添加或者删新元素,其他节点高度不变问题也不大了。
而且惊人的是,如果我们对新插入节点的高度进行随机产生(每次随机大于p,接着往上加高度,小于p停下来),然后别的节点高度保持不变,查找效率还是为O(logn),不会出现像二叉查找树那种直接退化成O(logn)的情况。
有兴趣想看推导的同学点个赞,点赞破100,咱写波推导。(目前面试还没卷到要证明跳表时间复杂度的程度,所以不知道咋推没问题)