本文转载自微信公众号「码工小熊」,作者小熊妹。转载本文请联系码工小熊公众号。
大家好,我是爱学习的小xiong熊妹。
之前分享了ABtest的基本原理,有小伙伴问:那如果我不止AB两个版本,而是有ABC三个版本做测试,还能用ABtest方法吗?当然能用!只是使用的统计学方法换成了:方差分析,今天简单跟大家分享一下。
一、多版本与AB两个版本的区别
如果只有AB两个版本比较,那么做假设检验的时候,原假设是:A版本均值/比例=B版本均值/比例。之后,只要我们能用测试结果推翻原假设,就能说明AB版本均值/比例不同,从而论证哪个版本更好。相应的统计量,也是依此设计的。
当有ABCDE……多个版本的时候,问题变得略复杂一些。因为很有可能这一堆版本里,有些有差异,有些没有。如果一个个测试,得对比n多次,费时费力。如何高效率的完成测试呢?
二、多版本测试基本思路
可以用两步骤方法:
第一步:先做方差分析,检验是否这几个版本的均值都是相等的。此时,原假设为:A版本=B版本=C版本=D版本……总之假设他们都是一样的。如果没有推翻该假设,则说明大家均值都一样,根本就不需要做第二步了。如果能推翻的话,再看其两两差距。
第二步:假设第一步检测已推翻原假设,则进行第二步检验。第二步可以用fisher LSD方法,对总体均值进行两两比较。
今天就先不啰嗦第二步检测了,我们先把第一步讲清楚。
三、方差分析是什么?
方差分析是用来检验多个版本(3个以上)对应的多组数据,是否存在均值差异的方法。方差分析的统计学原理略复杂,小伙伴们可以简单记忆为:用一个F统计量,衡量各组数据的组间差异与组内差异的比值。
当组间差异很大,组内差异很小的时候,则F统计量变得很大,说明这些样本肯定来自不同个体,从而不可能均值都相等,推翻原假设(如下图所示)
四、方差分析如何做
方差分析分为三步:
- 第一步:清晰要对比的版本
- 第二步:清晰要对比的数据指标
- 第三步:收集不同版本的测试数据
- 第四步:计算F统计量值,进行假设检验
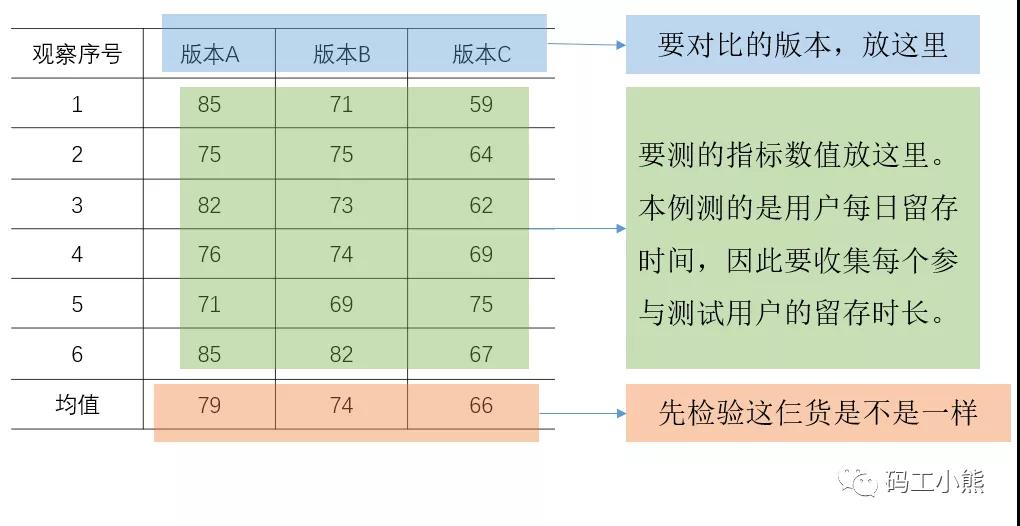
看个简单的例子:产品给个ABC三个版本,测试不同用户每日留存时间。每个版本各单独抽6名随机用户进行测试,数据如下:
- 第一步:确认要参与对比的是ABC版本
- 第二步:确认要比的指标是:三个版本下,用户每日留存时间
- 第三步:筛选用户,发布版本,收集测试数据(这里说的轻松,实际上涉及相当多的开发工作,之后有机会再详细讲)
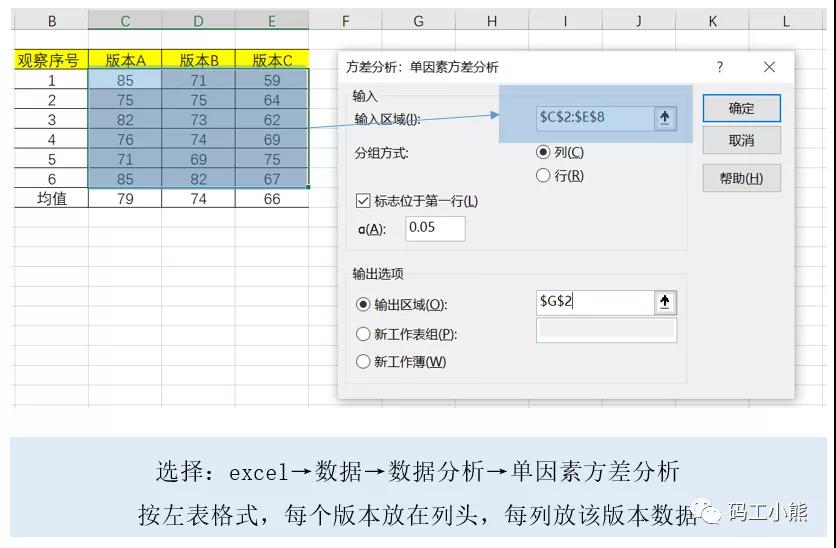
- 第四步:进行计算。这种只考虑“版本”一个影响因素的实验,称为:单因素方差分析,用excel都能求解(如下图)
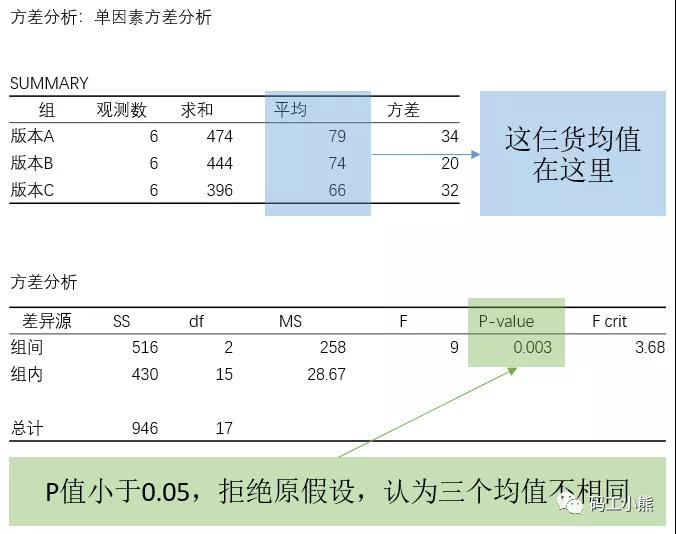
解出来数据如下图:
那么,可以认为这三组测试结果均值不同,能做第二步检验了。想偷懒的同学,可以直接认为版本C更差劲,先踢出去。
五、方差分析扩展
小伙伴们掌握了方差分析的思路以后,就能做很多对比。实际上,这种区分N个组别,测试版本/方法/属性对某个指标影响的做法,是数据实验的基本方法。通过不断地实验,能测试出新版本/新方法到底能起多大作用。
同时,方差分析也有进一步的应用。比如本例中,很有可能不同用户本身也有行为差异,需要从用户行为中剔除个人差异(比如让一个人体验三个版本)或者提前找到一些影响结果的因素(比如是否重度用户)然后将同类人组成一组。这些都是进一步设计实验要考虑的。
或者,影响结果的不止一个因素。用户用的久,除了版本影响外,还和运营动作,促销活动等有很大关系,因此可能需要对多个因素进行分析,此时又需要用到更复杂的方法。