最近,EMNLP 2021开奖了!华人作者包揽了最佳长、短论文。
然而,有人欢喜有人忧。
北大博士生沈剑豪领衔的一篇关于「用语言模型来解决数学应用题」(Generate & rank: A multi-task framework for math word problems)的EMNLP投稿在综合评审时被认为不够重要,最终收录于Findings而没有被主会接收。

「审稿人普遍喜欢这篇论文,但这看起来是一篇边缘的论文。鉴于这是BART在数学问题上的应用,而数学问题的解决对于NLP来说并不是一个真正重要的任务,我怀疑这个任务的高度工程化解决方案的价值。」
根据官方的文件来看,一般被列为Findings的论文得分会更低一些,或者被认为不怎么「新颖」。

拓展了特定任务的SOTA,但是对EMNLP社区而言,没有新的见解或更广泛的适用性;
有良好的、新颖的实验,并提出了全面的分析和结论,但使用的方法不够「新颖」。
虽然,但是OpenAI觉得这个论文很重要
有趣的是,就在10月29号,OpenAI提出了一个新方法「验证」(verification),声称可以解决小学数学问题。

论文地址:https://arxiv.org/pdf/2110.14168.pdf
GSM8K数据集地址:https://github.com/openai/grade-school-math
OpenAI要解决的数学应用题是长这个样子滴:

OpenAI的GSM8K数据集中的三个问题示例,红色为计算的注释
而且,OpenAI发现「验证」可以让60亿参数的GPT-3,解数学应用题的准确率直接翻倍,甚至追平了1750亿参数,采用微调方法的GPT-3模型。
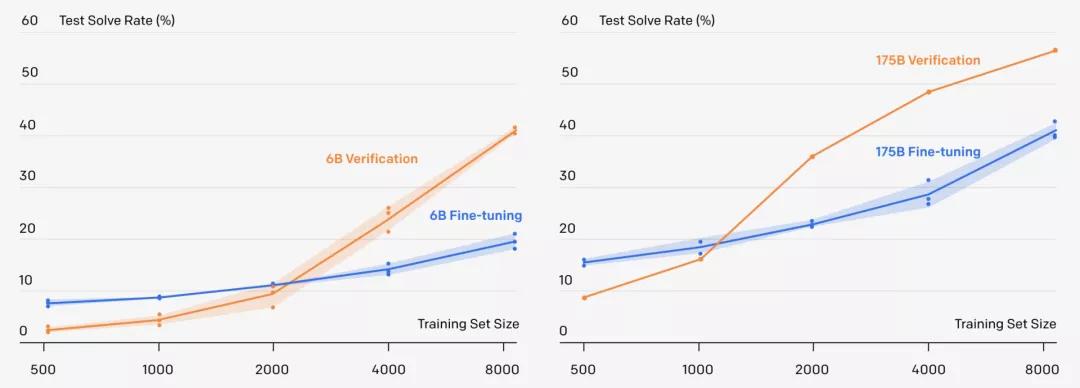
更重要的是,一个9-12岁的小孩子在测试中得分为60分,而OpenAI的方法在同样的问题上可以拿到55分,已经达到了人类小学生90%左右的水平!
都是解决数学应用题,那会不会这两篇文章是「异曲同工」呢?
巧了,还真是!
不仅如此,OpenAI这个最新工作《Training Verifiers to Solve Math Word Problems》文中还引用了北大博士生沈剑豪在9月7号提交的《Generate & Rank: A Multi-task Framework for Math Word Problems》这篇论文。

沈剑豪,尹伊淳,李琳,尚利峰,蒋欣,张铭, 刘群,《生成&排序:一种数学文字问题的多任务框架》,EMNLP 2020 Findings。该工作由北大计算机学院和华为诺亚方舟实验室合作完成。
论文地址:https://arxiv.org/abs/2109.03034
再看看沈同学文中要解决的数学应用题长啥样。
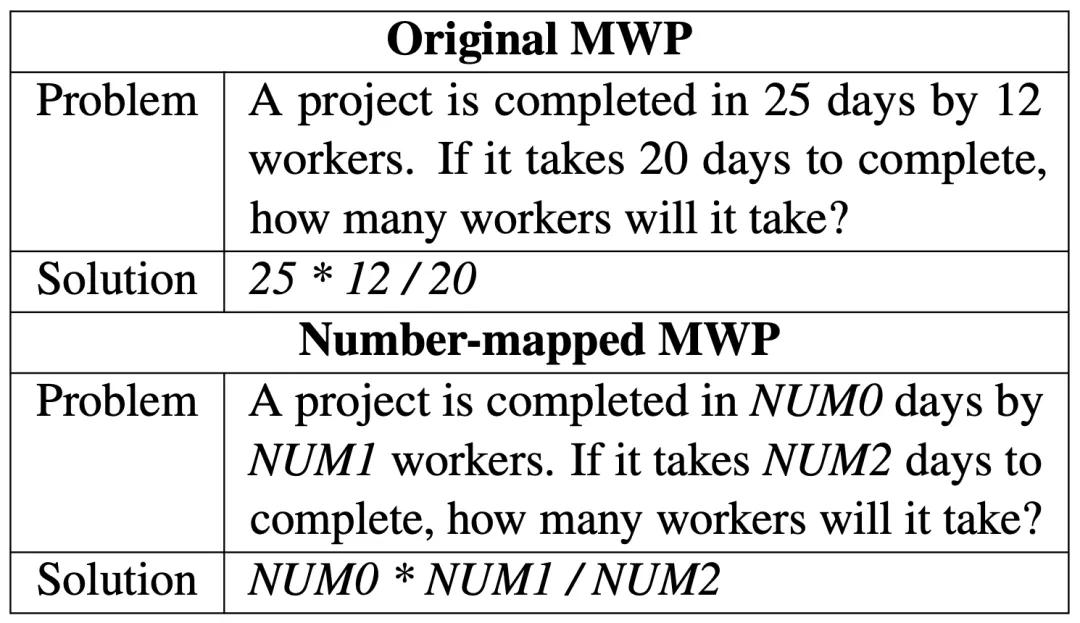
两者确实很像啊!
深入OpenAI的论文的Introduction部分,可以找到下面这句话。
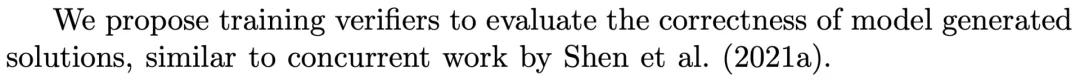
OpenAI在论文中表示其思路和沈剑豪的论文相似
在Related Methods中,还可以看到下面这句。

我们的工作与他们的方法有许多基本相似之处,尽管我们在几个关键方面有所不同。
在文末,OpenAI也对沈博士的文章注明了引用。

也就是说,OpenAI认可了沈同学文中的方法的价值,而且沈剑豪的论文其实比OpenAI还要早发一个月!
值得一说的是,这篇论文的一作沈剑豪是2014年浙江省高考状元,同时也曾是北大数学学院数据方向的第一名,目前是北大计算机学院在读博士研究生,导师为张铭教授。
语言模型能解数学题吗?
OpenAI的GPT-3「文采出众」,上知天文,下知地理。模仿名家的写作风格,展示一下广博的知识,这都不在话下。
然而,GPT-3这种「语言」模型却是典型的偏科生,擅长文,但不擅理,没法完成精确的多步推理,比如,解决小学数学应用题。
其问题就在于,语言模型只能模仿正确解决方法的规律,但它却并不理解「逻辑」。
所以,人类要想教会大语言模型理解复杂的逻辑,就必须得让模型学会识别它们的错误,并仔细选择他们的解题步骤。
从这个角度出发,OpenAI和博士生沈剑豪都提出了一种「先生成,后排序」的方法来帮助语言模型掌握数学推理能力,知道自己推理是否有误。
两者内容对比
核心框架是:生成器+重排序/验证器。
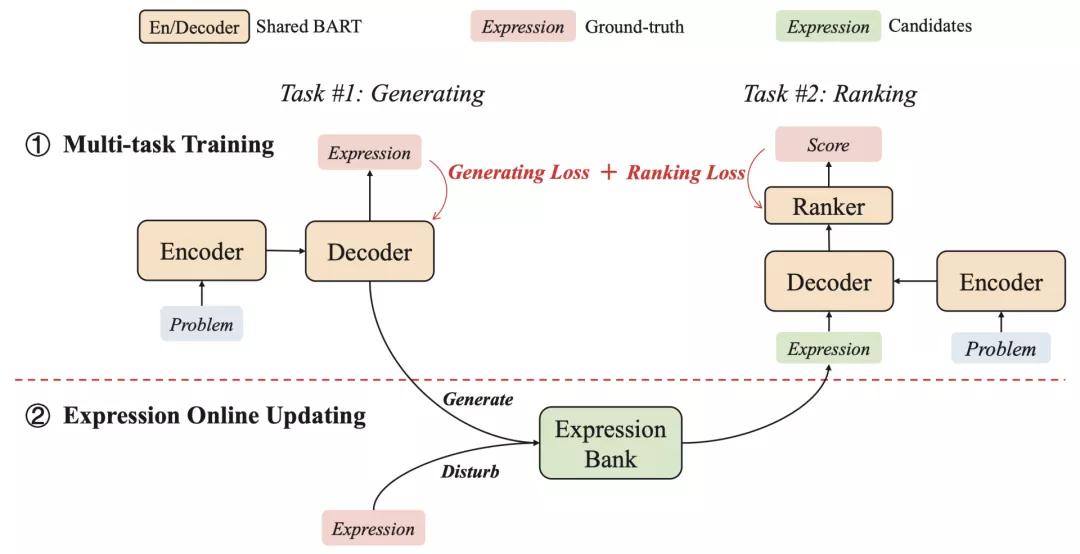
北大与华为诺亚的生成与重排序框架
沈同学文中的模型由一个生成器和一个排序器组成,并通过生成任务和排序任务进行联合训练。
生成器的目标是生成给定数学应用题的解答表达式。排序器则需要从一组候选者中选择一个正确的表达式。
两者共享同一个的BART模型进行编码-解码,排序器在此基础上增加了一个评分函数为表达式打分。
此外,他们还构建了一个表达式库,为排序器提供训练实例。其中使用了两种不同的策略:基于模型的生成和基于树的干扰。
基于模型的生成是利用生成器通过线束搜索方法,得到前K个表达式加入到表达式库中。
基于树的干扰则首先将正确表达式转化成一棵二叉树,然后采用扩展、编辑、删除、交换四种操作得到新的表达式,作为前一种方法的补充。
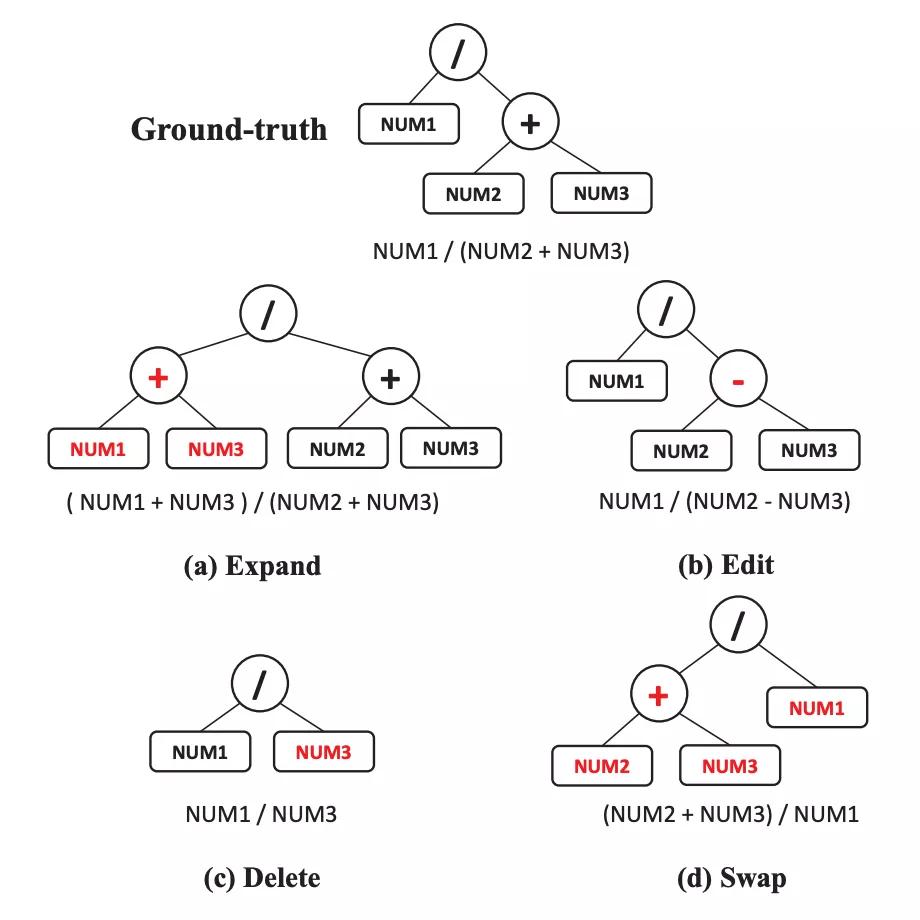
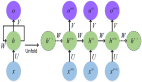
基于树的干扰
训练过程包括多任务训练和表达式在线更新。首先为生成任务对预训练的BART进行微调。之后,使用经过微调的BART和基于树的干扰来生成表达式,作为排序器的训练样本。然后,进行生成和排序的联合训练。
这个过程是以迭代的方式进行的,两个模块(即生成器和排序器)继续相互促进。同时,用于排序器的训练实例在每轮迭代后会被更新。

Generate & Rank的训练过程
而OpenAI的方法中是包含一个生成器和一个验证器。
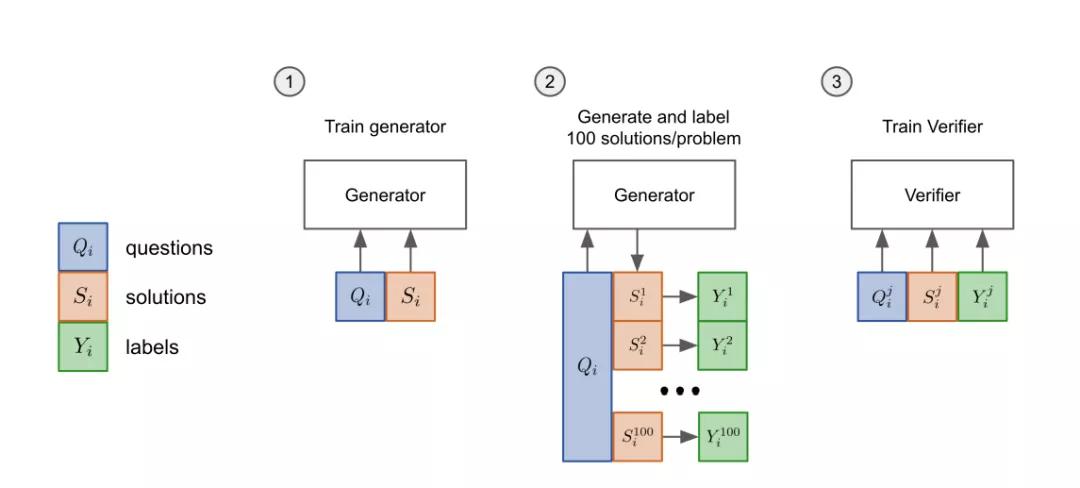
OpenAI的验证器
验证器(verifier)可以判断模型生成的解决方案正不正确,所以在测试时,验证器会以问题和候选解答为输入,输出每个解答正确的概率。验证器(verifier)训练时,只训练解决方案是否达到正确的最终答案,将其标记为正确或不正确。
验证器具体训练方法分「三步」:
- 先把模型的「生成器」在训练集上进行2个epoch的微调。
- 从生成器中为每个训练问题抽取100个解答,并将每个解答标记为正确或不正确。
- 在数据集上,验证器再训练单个epoch。
测试时,解决一个新问题,首先要生成100个候选解决方案,然后由「验证器」打分,排名最高的解决方案会被最后选中。
思路上确实是相近的,不过有几处细节并不相同。
一、OpenAI在文中表示他们的生成器和验证器是分开单独训练的,目的是限制生成器的训练并防止过度拟合,但原则上,他们认为应该可以组合这些模型进行联合训练,而沈同学则确实是使用了联合训练方法,实验结果也表明联合训练对最终的效果有提升。
二、沈同学提出了一种帮助训练重排器的方法:Tree-based Disturbance,其实就是设计了一系列比较难的负样本,在正确的表达式基础上增加了一点小扰动作为新的负样本。而OpenAI并没有提到类似的过程。
三、OpenAI为了评估「验证器」的表现,收集了全新的「GSM8K数据集」并将其开源以方便研究。
GSM8K由8500个高质量、高多样性、中等难度的小学数学问题组成。数据集中的每个问题都需要计算2到8个步骤来得出最终答案,涉及到「加减乘除」四则运算。
而沈同学最终是在两个常用的数据集上进行了实验:Math23K和MAWPS。
其中,Math23K是一个大规模的中文数据集,包含23162个数学应用题及其对应的表达式求解。MAWPS是一个包含2373个问题的英语数据集,所有的问题都是一个未知变量的线性问题,可以用一个表达式来解决。
当然,最明显的就是用的语言模型不同了。沈同学用的是预训练模型BART,而OpenAI用的则是60亿和1750亿参数的GPT-3。