大家好,我是Python进阶者。
是不是觉得很诧异?明明上周刚发布了这篇:分享一道用Python基础+蒙特卡洛算法实现排列组合的题目(附源码),今天又来一篇,名曰番外篇!其实今天是想给大家分享【🌑(这是月亮的背面)】大佬的解法,拍案叫绝!
前情回顾
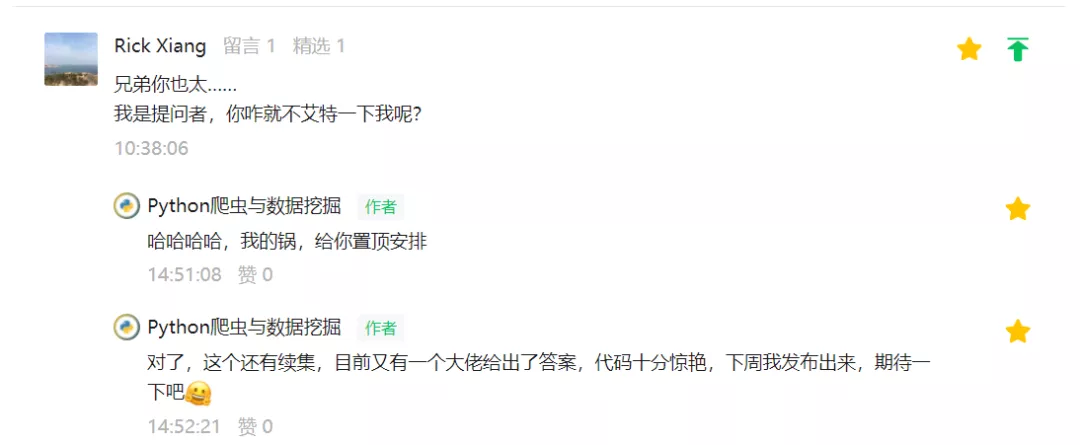
前几天在才哥交流群里,有个叫【Rick Xiang】的粉丝在Python交流群里问了一道关于排列组合的问题,初步一看觉得很简单,实际上确实是有难度的。
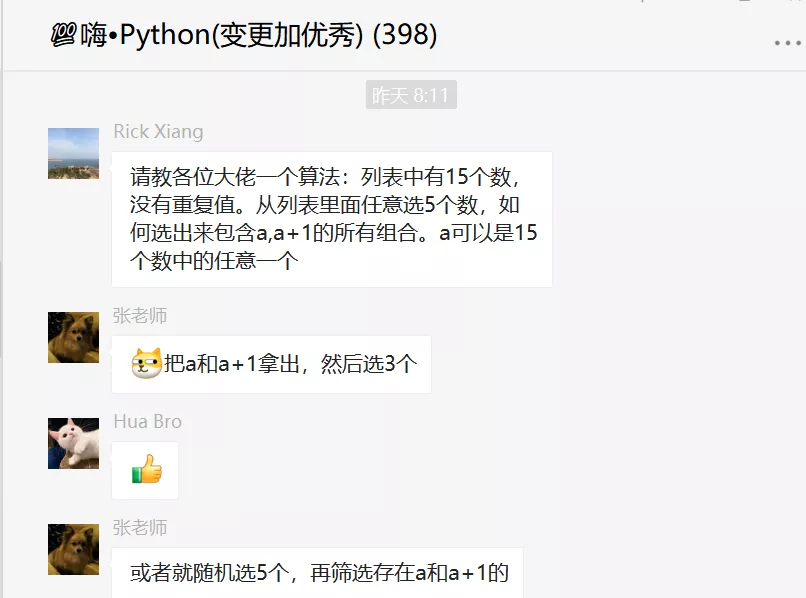
题目是:一个列表中有随机15个数,没有重复值。从列表里面任意选5个数,如何选出来包含a, a+1的所有组合。a可以是15个数中的任意一个。
关于思路和解决方法,这篇文章分享一道用Python基础+蒙特卡洛算法实现排列组合的题目(附源码)中提供了【张老师】和【有点意思】大佬的想法和解决方案,一共有5份代码,足够大家学习了,感兴趣的小伙伴快去学习吧,干货满满。
二、新代码
上周五的时候,发布了这篇分享一道用Python基础+蒙特卡洛算法实现排列组合的题目(附源码)原创文章,很庆幸还有粉丝亲自实践,并给出了建设性的方案,如下图所示。
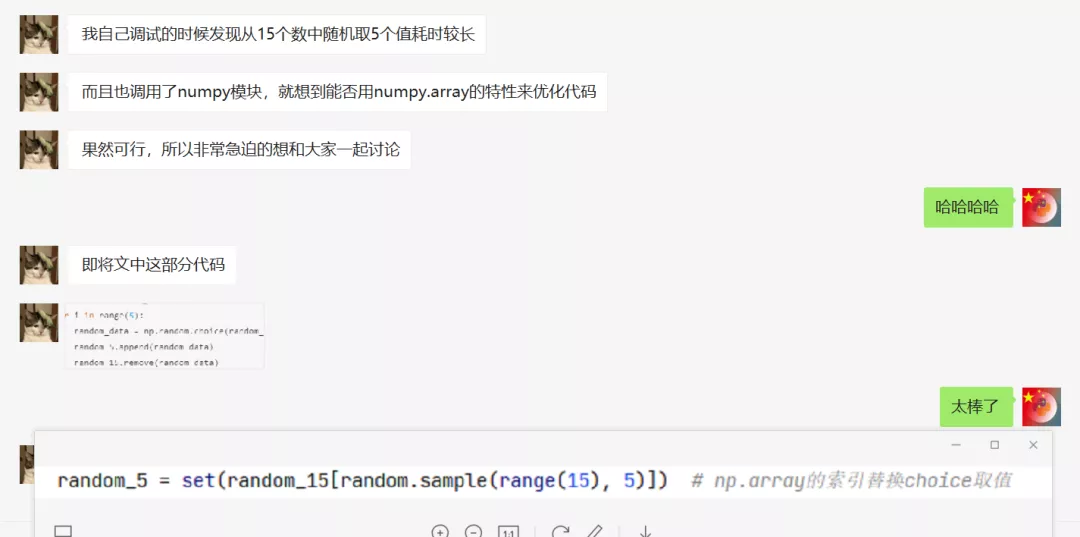
这里先给出【🌑(这是月亮的背面)】大佬的伪代码,这样看上去大家也更加好理解一些。
- # -*- coding: utf-8 -*-
- # 模块化
- import random
- import numpy as np
- import time
- # 取出随机的15个数值
- def get_random15():
- random_array = [np.array(random.sample(range(2000), 15)) for i in range(100000)]
- random5 = {get_random5(random15) for random15 in random_array}
- return [i for i in random5 if i]
- # 遍历随机的15个数值,取相邻的两个随机数,判断后返回满足条件的值
- def get_random5(random_15):
- random_5 = set(random_15[random.sample(range(15), 5)]) # np.array的索引替换choice取值
- # 利用set特性判断元素是否含有给定的元素
- random_5_resp = {True if len(random_5.intersection({num, num + 1})) == 2 else False for num in random_5}
- return tuple(random_5) if True in random_5_resp else ()
- if __name__ == '__main__':
- start_time = time.time()
- final_result = get_random15()
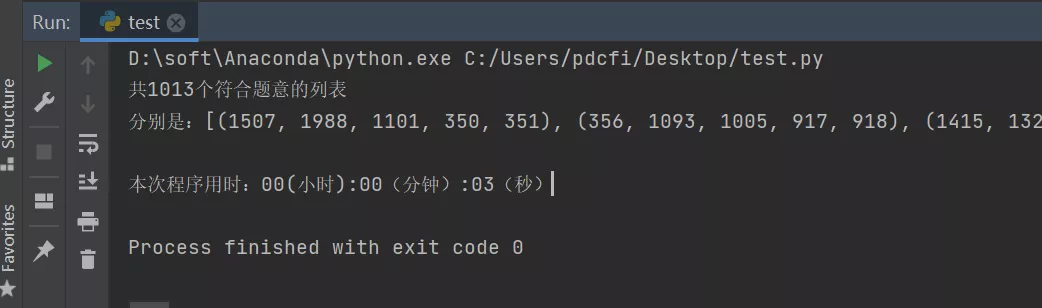
- print("共%d个符合题意的列表" % len(final_result))
- print("分别是:%s" % final_result)
- end_time = time.time()
- used_time = end_time - start_time
- print()
- print("本次程序用时:{}".format(time.strftime('%H(小时):%M(分钟):%S(秒)', time.gmtime(used_time))))
这个代码写的真的很好,没有Python基础的小伙伴看上去肯定有些吃力的,小编自己初看的时候,也觉得有点难以吸收,需要多看几遍,领悟。
这个代码亲测有效,用之前的代码大概需要12秒,改用这个只需要1.5秒。
他这里做了三个优化,其一是之前从15个数中随机取5个值耗时较长,这里用使用了numpy.array的特性来优化代码,在科学计算中,可以省掉很多循环语句,代码使用方面比Python列表简单,Python list 无法直接运算, Numpy Array 可直接运算;其二是删除了之前的去重函数,这里他也用set去优化,所以在这块也节约了时间;其三是使用了集合的交集运算(Intersection),较之前的if判断来说,节约了时间。
想到这里,不得不感叹一下,【人生苦短,我用python】!
三、总结
我是Python进阶者。本文基于粉丝针对排列组合问题的提问,给出了一个利用Python基础+蒙特卡洛算法的解决方案,基本上可以达到了粉丝的要求。
不过话说回来,这个方案虽是当下最优,但不是永远最优。