20张图带你搞懂十大经典排序算法-八大排序算法图解

[[433768]]

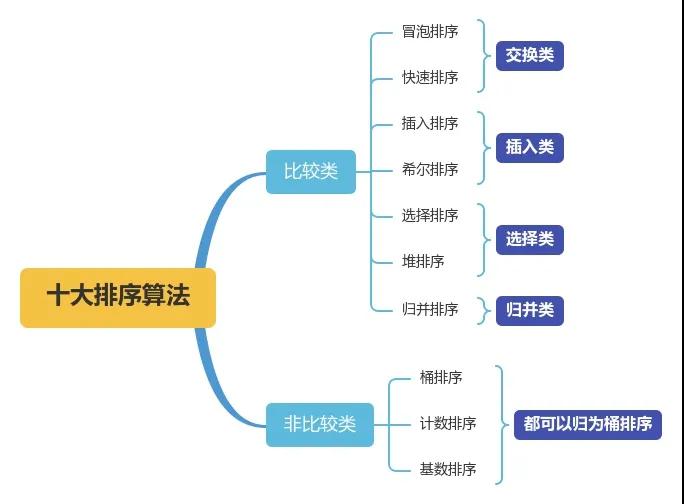
十大排序算法思路汇总

在面试的过程中经常会遇到手写排序算法，所以本文就简单总结一下。不对算法的细节做介绍，只做一个概括性的描述。

交换类：通过元素之间的两两交换来实现排序

插入类：将数分为2部分，依次将无序的数插入到有序的数列中

选择类：从待排序数列中找到最小值或者最大值元素，放到已拍好序的序列后面

「计数排序和基数排序可以认为是桶排序的一种特殊实现，都不是通过元素之间的比较来实现排序的」

冒泡排序

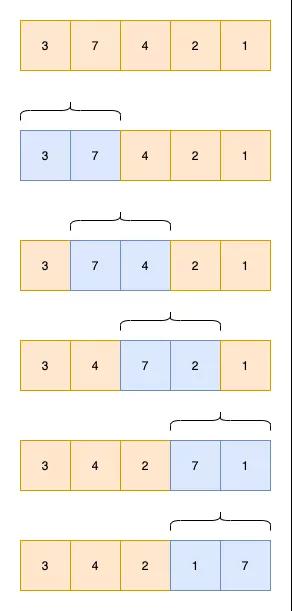
冒泡排序，从头开始，依次比较数组中相邻的2个元素，如果后面的数比前面的数大，则交换2个数，否则不交换。每进行一轮比较，都会把数组中最大的元素放到最后面。

如下图，一轮比较的过程如下

当数组中有n个元素时，只需要进行n轮比较，则整个数组就是有序的

public static void bubbleSort(int[] a) { 
 // 进行i轮比较 
    for (int i = 0; i < a.length - 1; i++) { 
        for (int j = 0; j < a.length - 1 - i; j++) { 
            if (a[j] > a[j + 1]) { 
                swap(a, j, j + 1); 
            } 
        } 
    } 
} 
 
public static void swap(int[] a, int i, int j) { 
    int temp = a[i]; 
    a[i] = a[j]; 
    a[j] = temp; 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.

快速排序

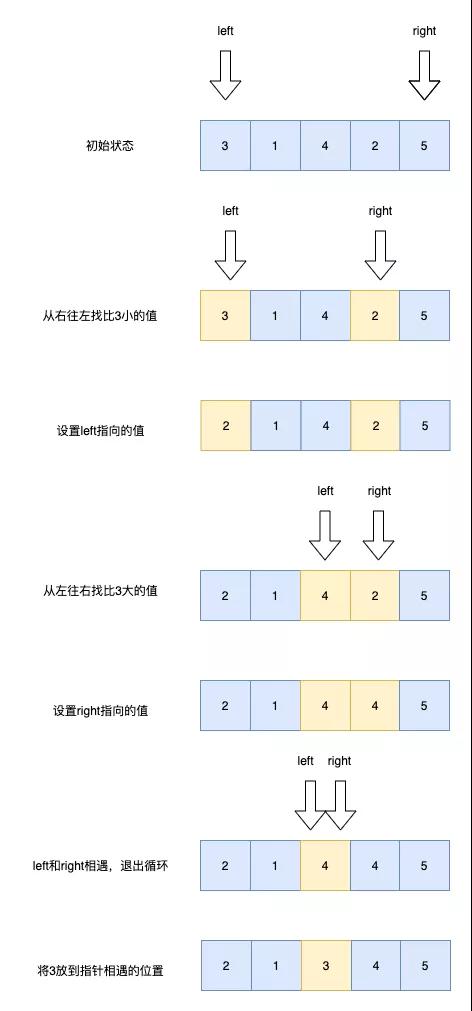
快速排序的执行流程主要分为如下三步

从数列中取出一个数作为基准数

分区，将比它大的数全放到它的右边，小于或等于它的数全放到它的左边

再对左右区间重复第二步，直到各区间只有一个数

public static void quickSort(int[] a, int left, int right) { 
    if (left >= right) { 
        return; 
    } 
    int index = sort(a, left, right); 
    quickSort(a, left, index - 1); 
    quickSort(a, index + 1, right); 
} 
 
public static int sort(int[] a, int left, int right) { 
    int key = a[left]; 
    while (left < right) { 
        // 从high所指位置向前搜索找到第一个关键字小于key的记录和key互相交换 
        while (left < right && a[right] >= key) { 
            right--; 
        } 
        a[left] = a[right]; 
        // 从low所指位置向后搜索，找到第一个关键字大于key的记录和key互相交换 
        while (left < right && a[left] <= key) { 
            left++; 
        } 
        a[right] = a[left]; 
    } 
    // 放key值，此时left和right相同 
    a[left] = key; 
    return left; 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.

下图演示了一次分区的流程

「经典的Top K面试题一般就可以用快排和堆排序来解决」。我们在下一节手写堆排序来分析吧

插入排序

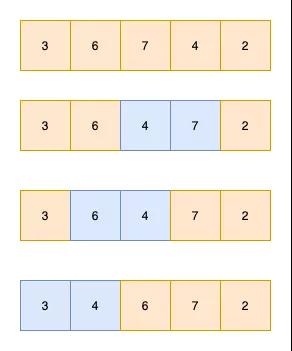
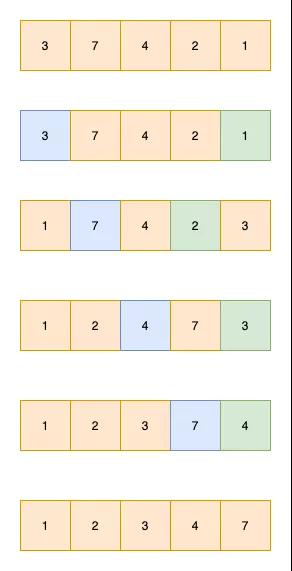
将数组分为2端，有序数组和无序数组，依次将无序数组中的值插入到无序数组中。

如下图3 6 7为有序数组，4 2为无序数组。依次将4，2插入到无序数组中即可

如图，插入4的过程如下

程序怎么划分有序数组和无序数组呢?可以认为第一个元素为有序数组，后面的值依次插入即可

public static void insertionSort(int[] a) { 
    for (int i = 1; i < a.length; i++) { 
        for (int j = i; j > 0; j--) { 
            while (a[j] < a[j - 1]) { 
                swap(a, j, j - 1); 
            } 
        } 
    } 
} 
 
public static void swap(int[] a, int i, int j) { 
    int temp = a[i]; 
    a[i] = a[j]; 
    a[j] = temp; 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

「可以看到有很多无用的交换位置的过程，我们可以先直接定位到要交换的元素，然后进行一次交换即可。改进后的插入排序代码」

public static void insertionSort(int[] a) { 
    for (int i = 1; i < a.length; i++) { 
        int temp = a[i]; 
        int j; 
        // 查到合适的插入位置，插入即可 
        for (j = i - 1; j >= 0 && a[j] > temp; j--) { 
            a[j + 1] = a[j]; 
        } 
        a[j + 1] = temp; 
    } 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.

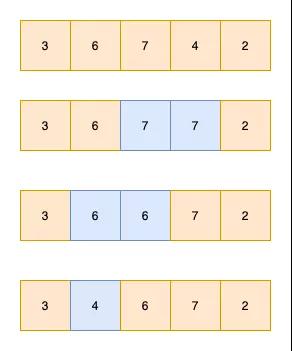
希尔排序

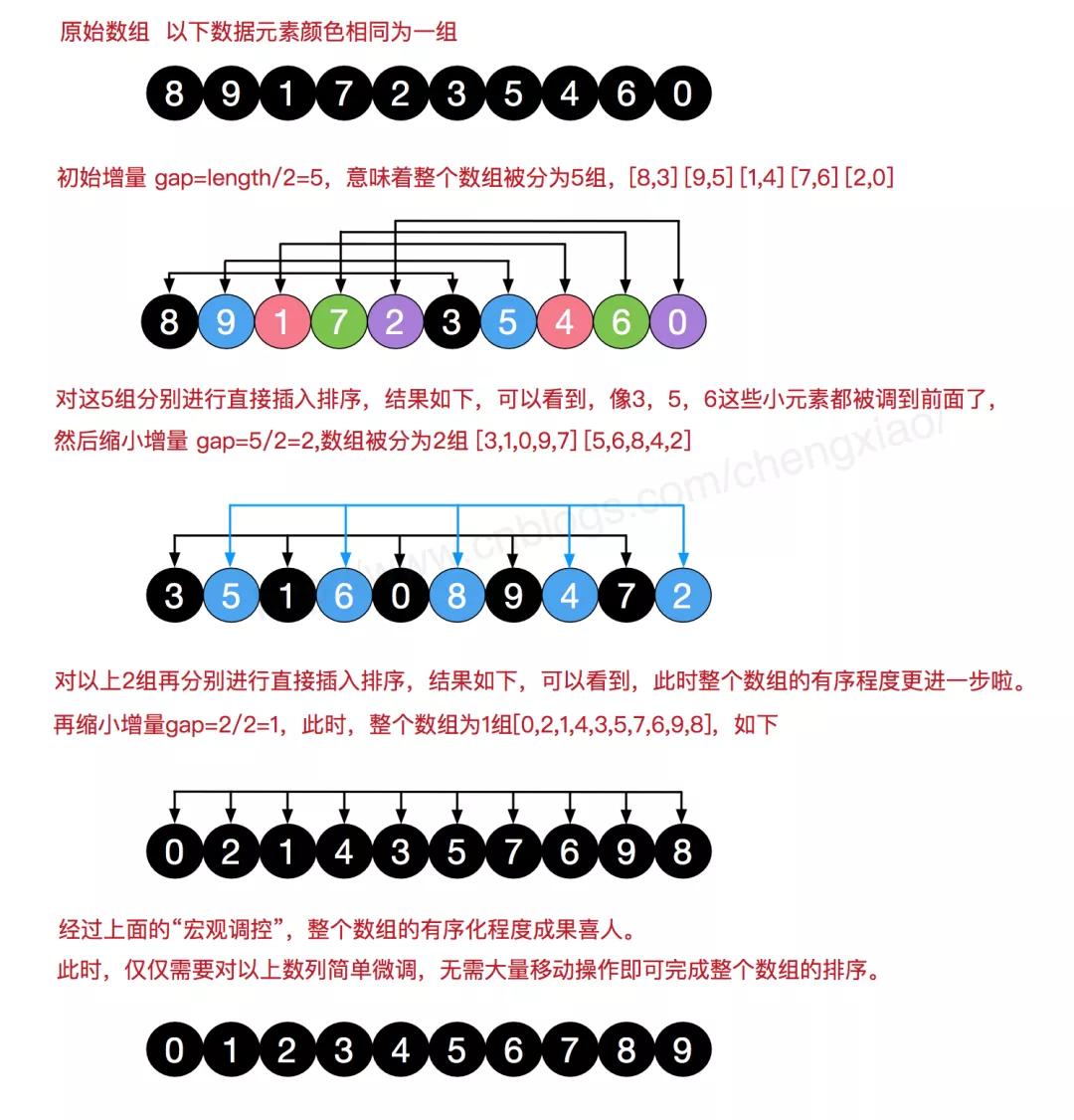
「希尔排序是基于插入排序改进后的算法。因为当数据移动次数太多时会导致效率低下。所以我们可以先让数组整体有序(刚开始移动的幅度大一点，后面再小一点)，这样移动的次数就会降低，进而提高效率」

原文地址：博客园《图解排序算法(二)之希尔排序》

public static void shellSort(int[] a) { 
    for (int step = a.length / 2; step > 0; step /= 2) { 
        for (int i = step; i < a.length; i++) { 
            int temp = a[i]; 
            int j; 
            for (j = i - step; j >= 0 && a[j] > temp ; j -= step) { 
                a[j + step] = a[j]; 
            } 
            a[j + step] = temp; 
        } 
    } 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.

选择排序

第一次迭代，将最小的放在数组第0个位置第二次迭代，将次小的放在数组第1个位置

public static void selectionSort(int[] a) { 
    for (int i = 0; i < a.length; i++) { 
        int index = i; 
        for (int j = i + 1; j < a.length; j++) { 
            if (a[index] > a[j]) { 
                index = j; 
            } 
        } 
        if (index != i) { 
            swap(a, index, i); 
        } 
    } 
} 
 
public static void swap(int[] a, int i, int j) { 
    int temp = a[i]; 
    a[i] = a[j]; 
    a[j] = temp; 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.

堆排序

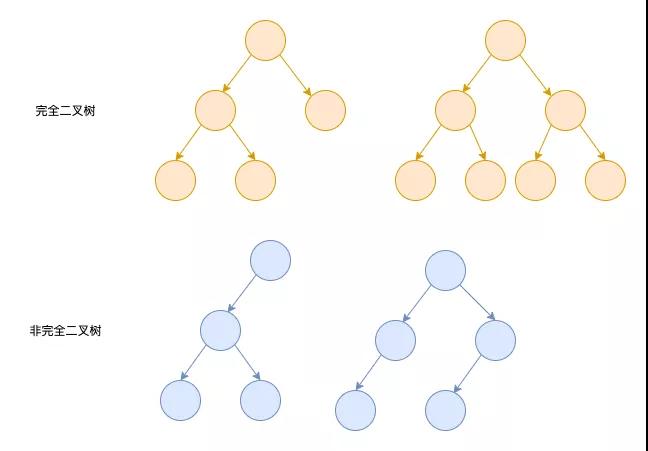
我们来手写一下堆排序，首先我们解释一下什么是堆?

堆是一种数据结构，需要满足如下几个特性
堆是一颗完全二叉树(生成节点的顺序是从左往右，从上往下依次进行)

堆中某个节点值总是不大于或者不小于其父节点的值

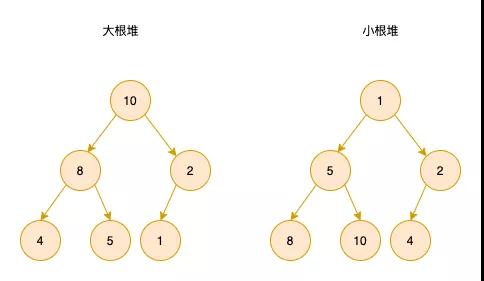
「将根结点最大的堆叫做最大堆或大根堆，根结点最小的堆叫做最小堆或小根堆」

大根堆和小根堆如下图所示

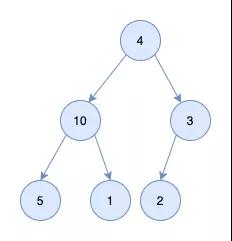
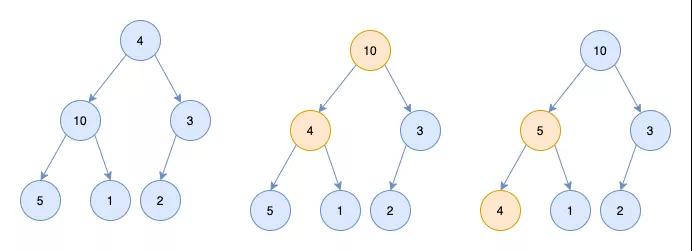
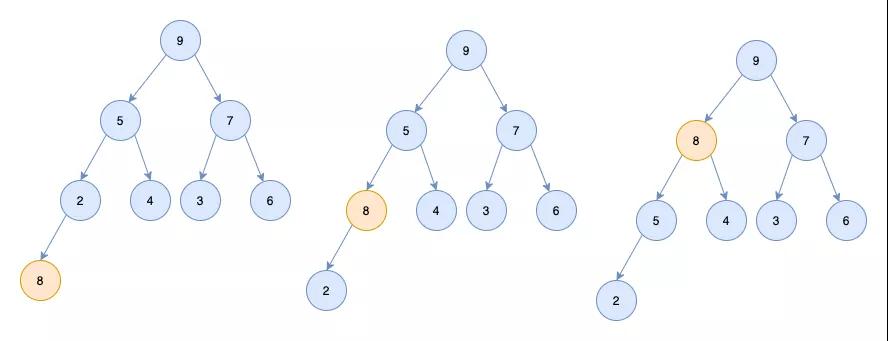
假设有如下一个完全二叉树，如何将它调整为一个堆呢?

可以看到10及其子节点符合条件，3及其子节点符合条件，4这个节点不符合条件。

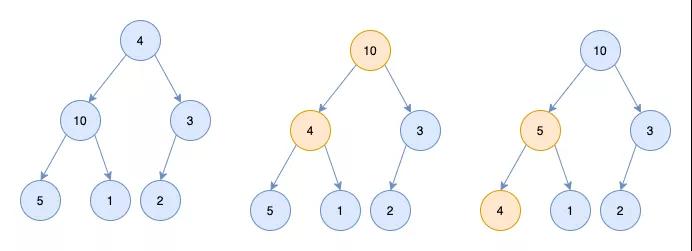
「所以要对4这个节点进行调整，调整的过程称为heapify」

从4这个节点的左右节点找一个大的节点(即10这个节点)和4这个节点进行交换
交换完有可能交换后的节点不符合条件，所以还需要进行调整(调整过程和1类似)
最终4节点和5节点进行交换。二叉树变为堆

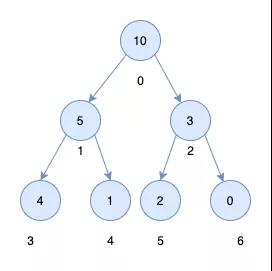
在实际开发的过程中，我们并不会用树这种结构来表示堆，而是用数组。通过下标的特点，可以总结出如下规律

假如一个节点在数组中的节点下标为i，则

父节点下标为：parent = (i - 1) / 2 左节点下标为：c1 = 2 * i + 1 右节点下标为：c2 = 2 * i + 2

所以上图中的堆，用数组表示为[10, 5, 3, 4, 1, 2, 0]

知道了如何用数组表示堆，我们写一下对如下4这个节点heapify的过程

/** 
 * @param a 数组 
 * @param n 数组长度 
 * @param i 要进行heapify的节点 
 */ 
public static void heapify(int[] a, int n, int i) { 
    // 递归出口 
    if (i >= n) { 
        return; 
    } 
    // 左节点下标 
    int c1 = 2 * i + 1; 
    // 右节点下标 
    int c2 = 2 * i + 2; 
    int max = i; 
    if (c1 < n && a[c1] > a[max]) { 
        max = c1; 
    } 
    if (c2 < n && a[c2] > a[max]) { 
        max = c2; 
    } 
    // 将左节点，右节点中的最大值和父节点交换 
    if (max != i) { 
        swap(a, max ,i); 
        heapify(a, n, max); 
    } 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.

@Test 
public void heapify() { 
    int[] array = new int[]{4, 10, 3, 5, 1, 2}; 
    // 调整后为 10， 5， 3， 4， 1， 2 
    HeapSort.heapify(array, array.length,0); 
1.
2.
3.
4.
5.

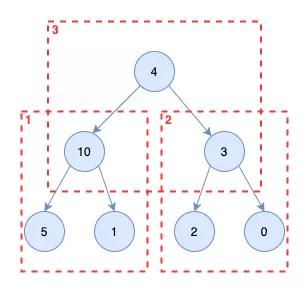
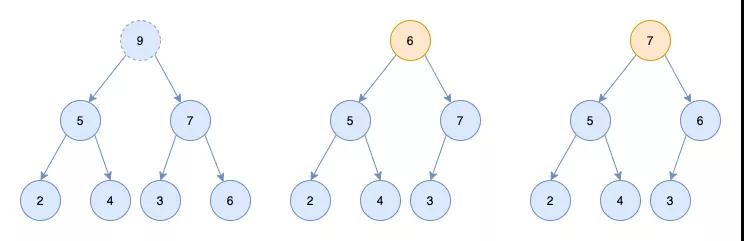
「我们如何把一个完全二叉树变为堆呢?」

「只要对非叶子节点从左边往右，从下到上依次进行heapify即可。」如下图只需要依次对10，3，4进行heapify即可

public static void buildTree(int[] a) { 
    // 找到最后一个非叶子节点 
    int lastNode = a.length - 1; 
    int parent = (lastNode - 1) / 2; 
    for (int i = parent; i >= 0; i--) { 
        heapify(a, a.length, i); 
    } 
} 
1.
2.
3.
4.
5.
6.
7.
8.

我们来测试一下

@Test 
public void buildTree() { 
    int[] array = new int[]{3, 5, 7, 2, 4, 9, 6}; 
    // 9 5 7 2 4 3 6 
    HeapSort.buildTree(array); 
} 
1.
2.
3.
4.
5.
6.

知道了堆是如何生成以及如何调整的过程，我们再分析堆排序的过程就非常简单了!

以大顶堆为例，最大值一定是根节点。

将根节点和最后一个叶子节点交换，然后将这个叶子节点移出堆
此时根节点是不符合要求的，所以对根节点进行heapify后，又变成了一个堆了
重复1，2步，就能找出剩余节点中的最大值

因为每次找出的最大值，都是在数组的最后一位，所以我们不需要真正的进行移除堆这个操作，只是进行heapify的时候，数组长度逐渐递减即可。最终的数组就是升序的

public static void heapSort(int[] a) { 
    // 先构建一个堆 
    buildTree(a); 
    // 每次将堆的根节点和最后一个节点进行交换，然后进行heapify 
    for (int i = a.length - 1; i >= 0; i--) { 
        swap(a, i, 0); 
        heapify(a, i, 0); 
    } 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.

所以最终一个堆排序的代码如下

public class HeapSort { 
 
    public static void heapSort(int[] a) { 
        buildTree(a); 
        for (int i = a.length - 1; i >= 0; i--) { 
            swap(a, i, 0); 
            heapify(a, i, 0); 
        } 
    } 
 
    public static void buildTree(int[] a) { 
        // 找到最后一个非叶子节点 
        int lastNode = a.length - 1; 
        int parent = (lastNode - 1) / 2; 
        for (int i = parent; i >= 0; i--) { 
            heapify(a, a.length, i); 
        } 
    } 
 
    /** 
     * @param a 数组 
     * @param n 数组长度 
     * @param i 要进行heapify的节点 
     */ 
    public static void heapify(int[] a, int n, int i) { 
        if (i >= n) { 
            return; 
        } 
        int c1 = 2 * i + 1; 
        int c2 = 2 * i + 2; 
        int max = i; 
        if (c1 < n && a[c1] > a[max]) { 
            max = c1; 
        } 
        if (c2 < n && a[c2] > a[max]) { 
            max = c2; 
        } 
        if (max != i) { 
            swap(a, max ,i); 
            heapify(a, n, max); 
        } 
    } 
 
    public static void swap(int[] a, int i, int j) { 
        int temp = a[i]; 
        a[i] = a[j]; 
        a[j] = temp; 
    } 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.

我们这里只演示了一下如何构建一个堆，以及堆排序的流程是怎样的?

「要实现一个完整的堆，我们还需要提供一个插入节点和删除根节点的方法」。我就不写实现了，用图演示一下流程，有兴趣的可以写一下，「大部分语言都会内置堆的实现，即优先级队列(Java中为PriorityQueue)，所以当我们有用到堆的场景时，直接用PriorityQueue即可」

堆插入节点

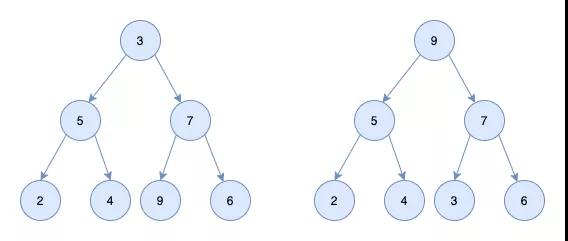
当堆插入节点时，插入的位置是完全二叉树的最后一个位置。比如我们插入一个新节点，值是8

我们让8和它的父节点比较，8>5，则让新节点上浮，和父节点交换位置

交换完后继续和父节点比较，8<9，则不用调整了

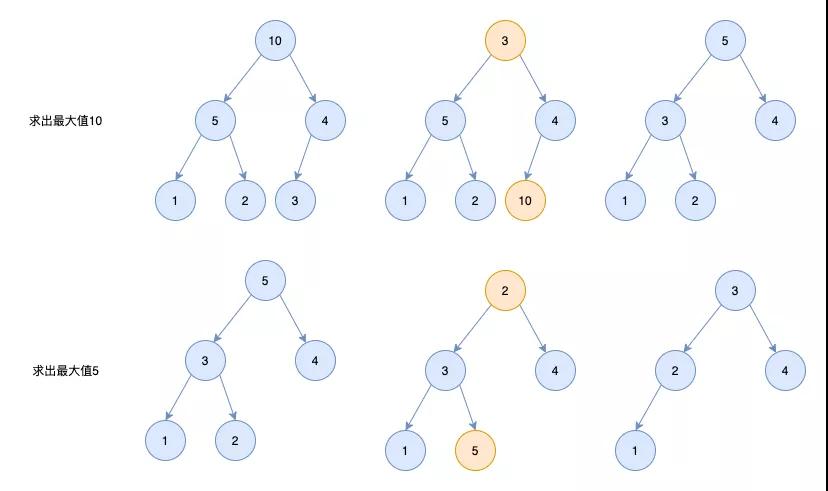
堆删除节点

堆删除节点时，删除的是堆顶的节点。比如我们删除大顶堆的9节点

为了维持堆的结构，我们把堆的最后一个节点6补到堆顶的位置

接着我们让堆顶的节点和它的左右孩子节点进行比较，如果左右孩子中最大的一个比节点6大，那么则让节点6下沉

接着和左右节点进行比较，3<6，则不用调整了

前 K 个高频元素

题目地址：剑指 Offer 40. 最小的k个数

输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。

输入：arr = [3,2,1], k = 2 
输出：[1,2] 或者 [2,1] 
1.
2.

限制：

0 <= k <= arr.length <= 10000 0 <= arr[i] <= 10000

「堆」

维护一个大顶堆当堆中的元素不够k时，一直往堆中放元素即可当堆中的元素大于等于k时，将堆顶的元素和新添加的元素进行比较。如果新添的元素比堆顶的元素小，则应该把堆顶的元素删除，将新填的元素放入堆，这样就能保证堆中的元素一直是最小的k个

public int[] getLeastNumbers(int[] arr, int k) { 
    if (arr.length == 0 || k == 0) { 
        return new int[0]; 
    } 
    PriorityQueue<Integer> queue = new PriorityQueue<>((num1, num2) -> num2 - num1); 
    for (int num : arr) { 
        if (queue.size() < k) { 
            queue.add(num); 
        } else if (num < queue.peek()) { 
            queue.poll(); 
            queue.add(num); 
        } 
    } 
    int[] result = new int[k]; 
    for (int i = 0; i < k; i++) { 
        result[i] = queue.poll(); 
    } 
    return result; 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.

「快速排序」

把快速排序的过程简单改一下就行了，我们根据基准值和k的的位置决定对左段还是右段进行排序即可，而不是对整个数组进行排序

class Solution { 
 
    public int[] getLeastNumbers(int[] arr, int k) { 
        if (arr.length == 0 || k == 0) { 
            return new int[0]; 
        } 
        return quickSort(arr, 0, arr.length - 1, k - 1); 
    } 
 
    public int[] quickSort(int[] nums, int left, int right, int k) { 
        int index = sort(nums, left, right); 
        if (index == k) { 
            return Arrays.copyOf(nums, k + 1); 
        } 
        // 根据 index 和 k 的位置决定切左段还是右段 
        return index > k ? quickSort(nums, left, index - 1, k) : quickSort(nums, index + 1, right, k); 
    } 
 
    public int sort(int[] a, int left, int right) { 
        int key = a[left]; 
        while (left < right) { 
            while (left < right && a[right] >= key) { 
                right--; 
            } 
            a[left] = a[right]; 
            while (left < right && a[left] <= key) { 
                left++; 
            } 
            a[right] = a[left]; 
        } 
        a[left] = key; 
        return left; 
    } 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.

「计数排序」

因为题目中有这样一个条件0 <= arr[i] <= 10000，说明数组中的元素比较集中，我们就可以用计数排序来解决这个问题，因为arr[i]的最大值10000为，所以我每次直接开一个10001大的数组

public int[] getLeastNumbers(int[] arr, int k) { 
    if (arr.length == 0 || k == 0) { 
        return new int[0]; 
    } 
    int[] countArray = new int[10001]; 
    for (int num : arr) { 
        countArray[num]++; 
    } 
    int[] result = new int[k]; 
    int index = 0; 
    for (int i = 0; i < countArray.length && index < k; i++) { 
        while (countArray[i] > 0 && index < k) { 
            countArray[i]--; 
            result[index++] = i; 
        } 
    } 
    return result; 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.

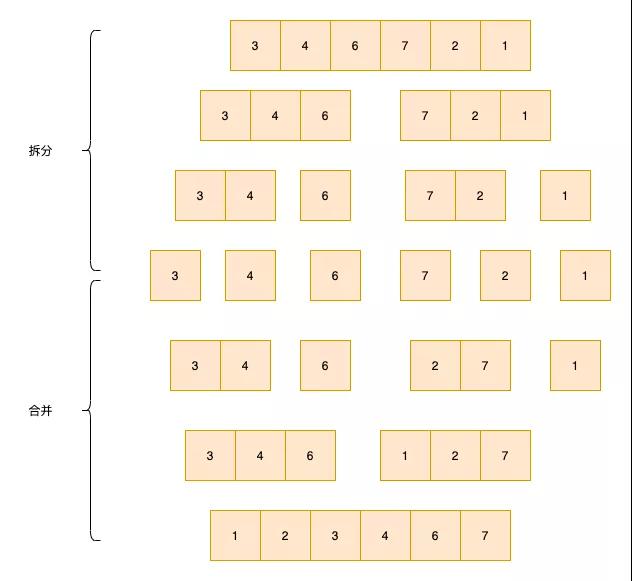
归并排序

先把数组拆分为只有一个元素，然后对拆分的数组进行合并，主要合并的时候要保证合并后的数组有序，当合并完成时，整个数组有序

public static void mergeSort(int[] a, int left, int right) { 
    // 将数组分段成只有一个元素 
    if (left == right) { 
        return; 
    } 
    int mid = (left + right) / 2; 
    mergeSort(a, left, mid); 
    mergeSort(a, mid + 1, right); 
    merge(a, left, mid, right); 
} 
 
public static void merge(int[] a, int left, int mid, int right) { 
    int[] temp = new int[right - left + 1]; 
    int i = left; 
    int j = mid + 1; 
    int k = 0; 
    while (i <= mid && j <= right) { 
        if (a[i] < a[j]) { 
            temp[k++] = a[i++]; 
        } else { 
            temp[k++] = a[j++]; 
        } 
    } 
    // 复制左边数组剩余的值 
    while (i <= mid) { 
        temp[k++] = a[i++]; 
    } 
    // 复制右边数组剩余的值 
    while (j <= right) { 
        temp[k++] = a[j++]; 
    } 
    int index = 0; 
    while (left <= right) { 
        a[left++] = temp[index++]; 
    } 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.

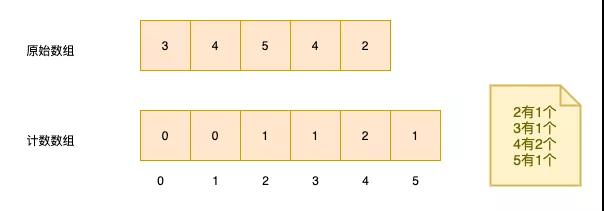
计数排序

新开辟一个数组，num[i]的含义为原数组中值为i的数有num[i]个。所以算法的局限性比较大，只适合数组元素跨度区间不大的场景。

public static void countingSort(int[] a) { 
    int max = Integer.MIN_VALUE; 
    for (int num : a) { 
        max = Integer.max(max, num); 
    } 
    int[] count = new int[max + 1]; 
    for (int num : a) { 
        count[num]++; 
    } 
    int index = 0; 
    for (int i = 0; i < count.length; i++) { 
        while (count[i] > 0) { 
            a[index++] = i; 
            count[i]--; 
        } 
    } 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.

上面的算法其实还有个缺陷，但数组中的元素为10000，10001，10002时，我们就得开辟一个10003大小的数组，不现实。所以我们可以改一下映射关系 num[i]的含义为原数组中值为i+min的个数为num[i]

进阶版

public static void countingSort(int[] a) { 
    int max = Integer.MIN_VALUE; 
    int min = Integer.MAX_VALUE; 
    for (int num : a) { 
        max = Integer.max(max, num); 
        min = Integer.min(min, num); 
    } 
    int[] count = new int[max - min + 1]; 
    for (int num : a) { 
        count[num - min]++; 
    } 
    int index = 0; 
    for (int i = 0; i < count.length; i++) { 
        while (count[i] > 0) { 
            a[index++] = i + min; 
            count[i]--; 
        } 
    } 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.

「面试过程中经常会遇到求一个数组中的众数时，就可以用计数排序的思想来解决」

基数排序

「面试过程中快拍和归并排序问的比较多，应用场景也比较多」，基数排序基本没被问到，不做解释了。

桶排序

「前面我们提到的计数排序和基数排序可以说是桶排序思想的一种特殊体现，就是不需要进行数组元素之间的比较」。基本没被问到，不做解释了

各种排序算法的应用

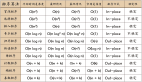
面试中常问的Top k问题，就可以先排序，然后求出Top k的元素。各种排序算法的效率如下图片「更高效的思路是用堆和快排。Top K问题问法很多，本质思路都一样，例如求前K个最大的元素，求前K个最小的元素，求前K个高频元素」

本文转载自微信公众号「Java识堂」，可以通过以下二维码关注。转载本文请联系Java识堂公众号。